2 Leíró statisztikai mutatók
2.1 Kategóriaváltozók kimutatásai
2.1.1 Gyakorisági táblák
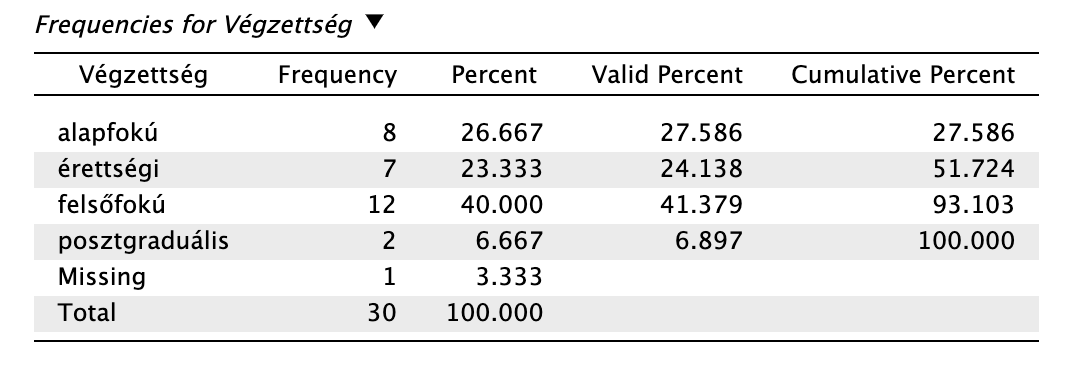
A gyakorisági tábla sorai az egyes kategóriákat jelzi (pl. végzettségi szint), mellettük feltünteti az adatsorunkban fellelhető darabszámokat az adott kategóriaszintből (pl. érettségi) abszolút gyakoriság (ti. darabszám) és relatív gyakoriság (ti. százalékos forma) szerint.
A relatív gyakoriság feltüntethető
- összes adat százalékban (Percent, ahol a hiányzó értékeknek is kiszámítjuk a relatív gyakoriságát),
- valid értékek százalékában (Valid Percent, ahol a hiányzó értékekhez nem rendelünk relatív gyakoriságot),
- kumulált százalékban (Cumulative Percent, ahol az alsóbb szintű relatív gyakoriságot hozzáadjuk a következő szint relatív gyakoriságához, és így a legutolsó kategória 100%-os relatív kumulált gyakorisági értéket vesz fel.)
JASP-ban egyszerűen tudunk ilyen ábrát létrehozni a Descriptive Statistics modul: Tables rovat Frequency tables funckiójával.
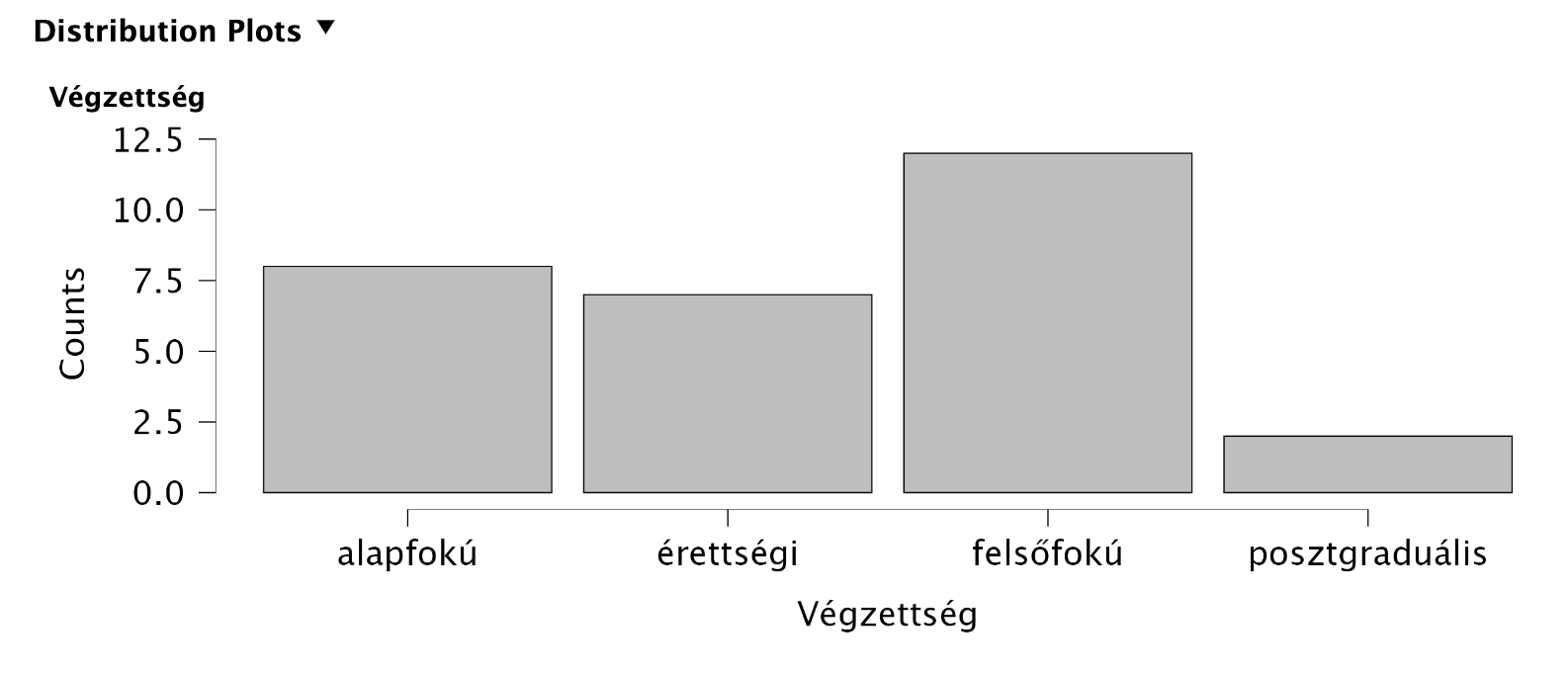
2.1.2 Hisztogram
Az egyes gyakoriságokat kategóriaváltozó esetén hisztogrammal tudjuk vizualizálni. Az x tengely tartalmazza a különböző kategóriákat, és oszlopok jelölik a gyakoriságot.
JASP-ban egyszerűen tudunk ilyen ábrát létrehozni a Descriptive Statistics modul: Basic Plots rovat Distribution plots funckiójával.
2.2 Skálaváltozók vizuális prezentációja
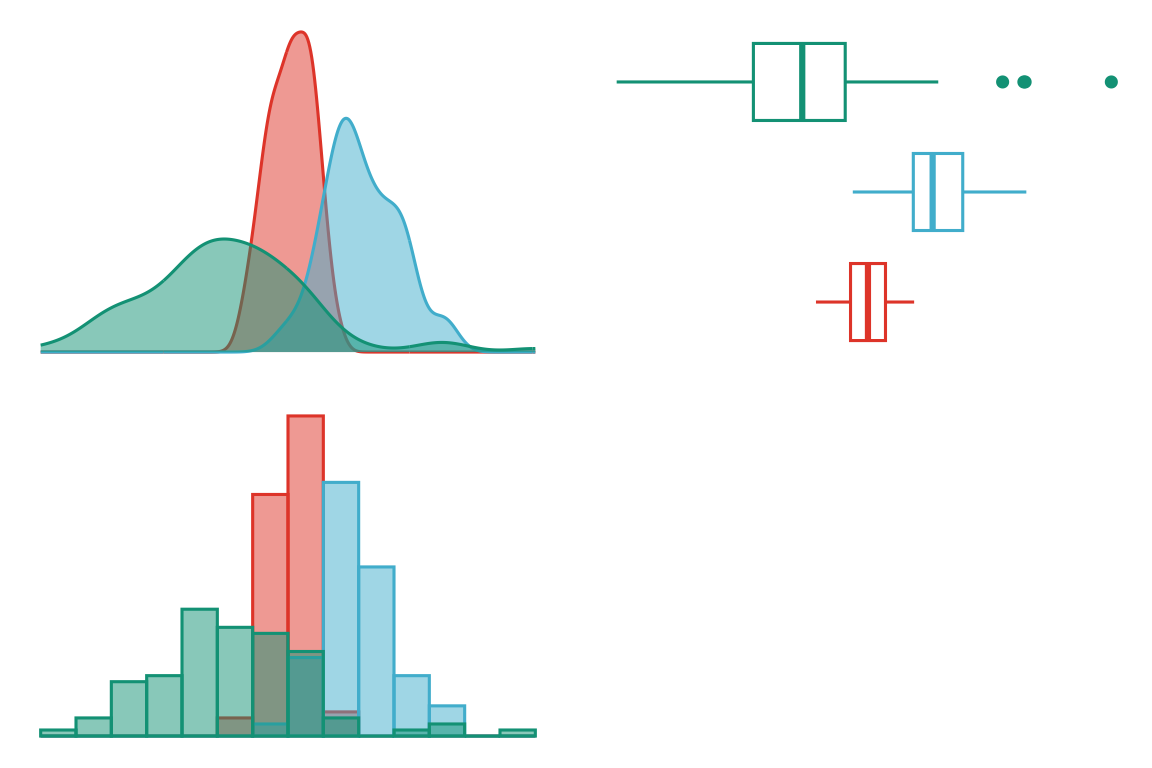
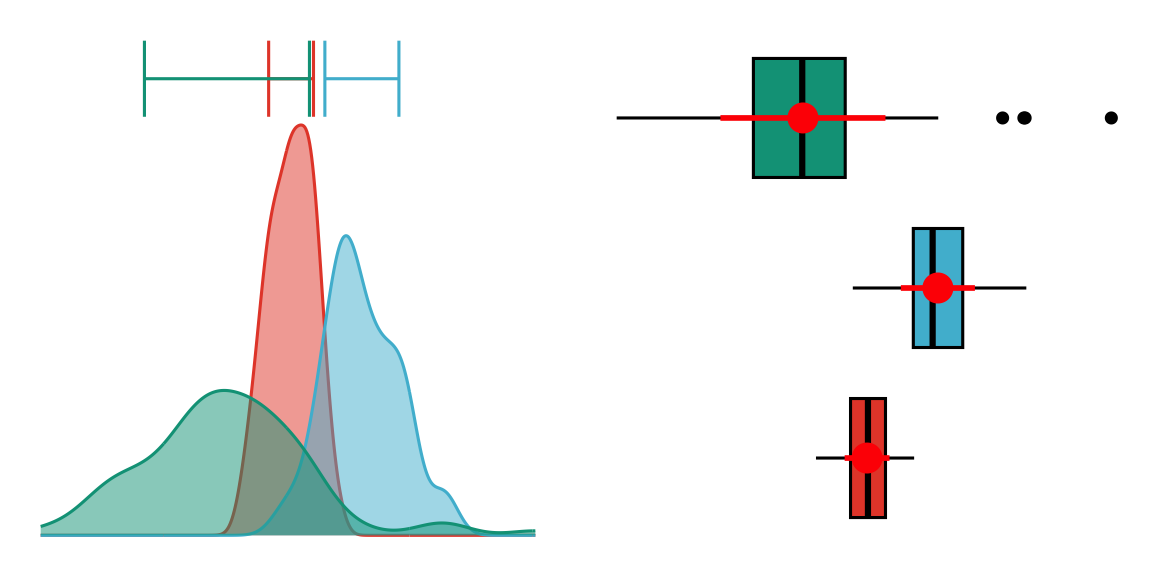
Folytonos adatainkat többek között hisztogrammal, sűrűségfüggvénnyel vagy boxplottal ábrázolhatjuk.
2.2.1 Boxplotok
A boxplotok vízszintes vagy függőleges formában készíthetők. A boxplot doboza az ábrázolt adatok 50%-át tartalmazza, egész pontosan az alsó kvartilis (Q1) és a felső kvartilis (Q3) közötti adatokat. A dobozok két oldalán találhatóak a boxplot bajszai, amelyek a minimum (Q0) és az alsó kvartilis (Q1), valamint a felső kvartilis (Q3) és maximum (Q4) közötti 25-25%-ot ábrázolja. Vegyük észre, hogy a boxplotok a kvartilisek meghatározásakor a kiugró vagy extrém értékeket külön ponttal jelölik. (Tehát a minimumot vagy maximumot a kiugró értékek nélkül ábrázolják.) A középső, dobozon belüli vonal a medián (Q2). Így összességében a boxplot kiválóan szemlélteti az adatok ferdeségét. Nem mutatja be azonban az adatok csúcsosságát, és nem szemlélteti, hogy egy globális vagy több lokális módusza van az adatsornak.
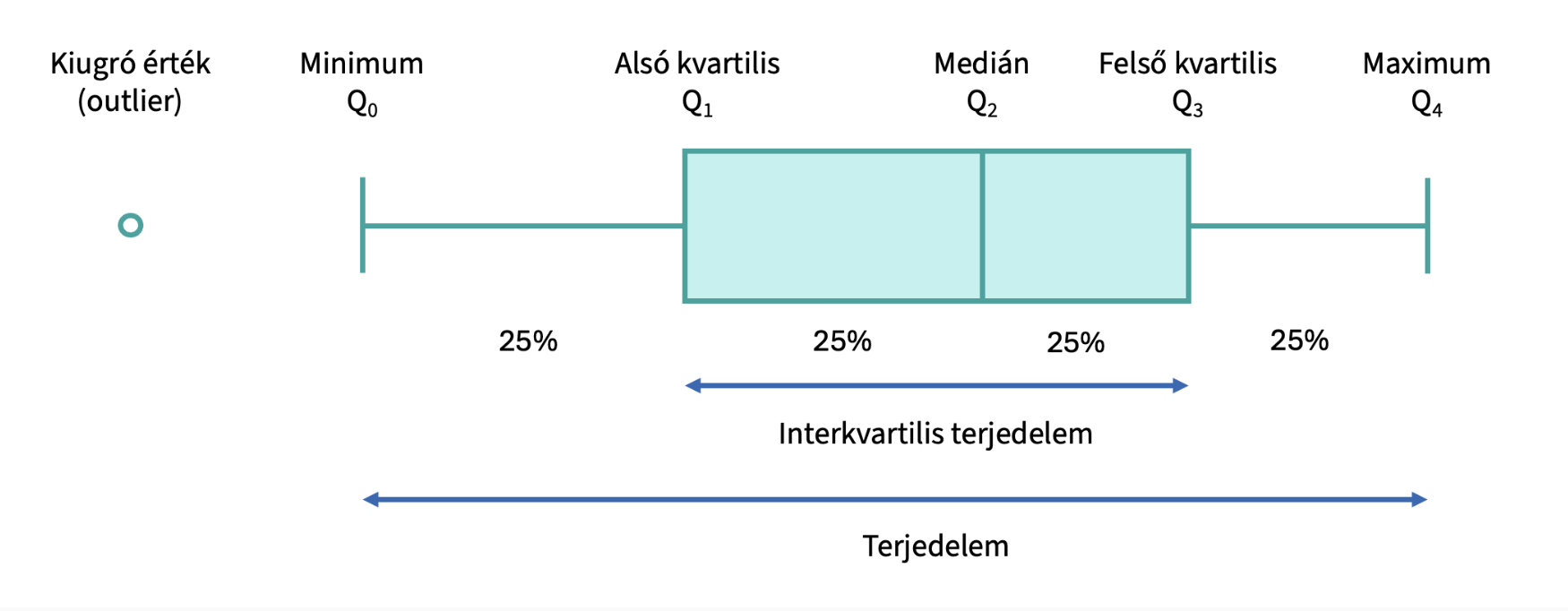
Boxplotot több JASP modul generál. A teljesség igénye nélkül:
Descriptive Statistics modul: Customizable Plots rovat Boxplots funckiója
Plot Builder (Beta) modul Distributions (histogram, boxplot, violin) rovatában (csak akkor ha van csoportosító változó is)
Egyes próbák kiegészítő funkcióként.
2.2.2 Hisztogram
A hisztogram alkalmas skálaváltozók vizualizációjára is, de ez esetben mégis diszkrét (véges) számú csoportokat kell alkotnunk az x tengelyen. (Ezt a JASP megteszi helyettünk.)
2.2.3 Sűrűségfüggvény (density plot)
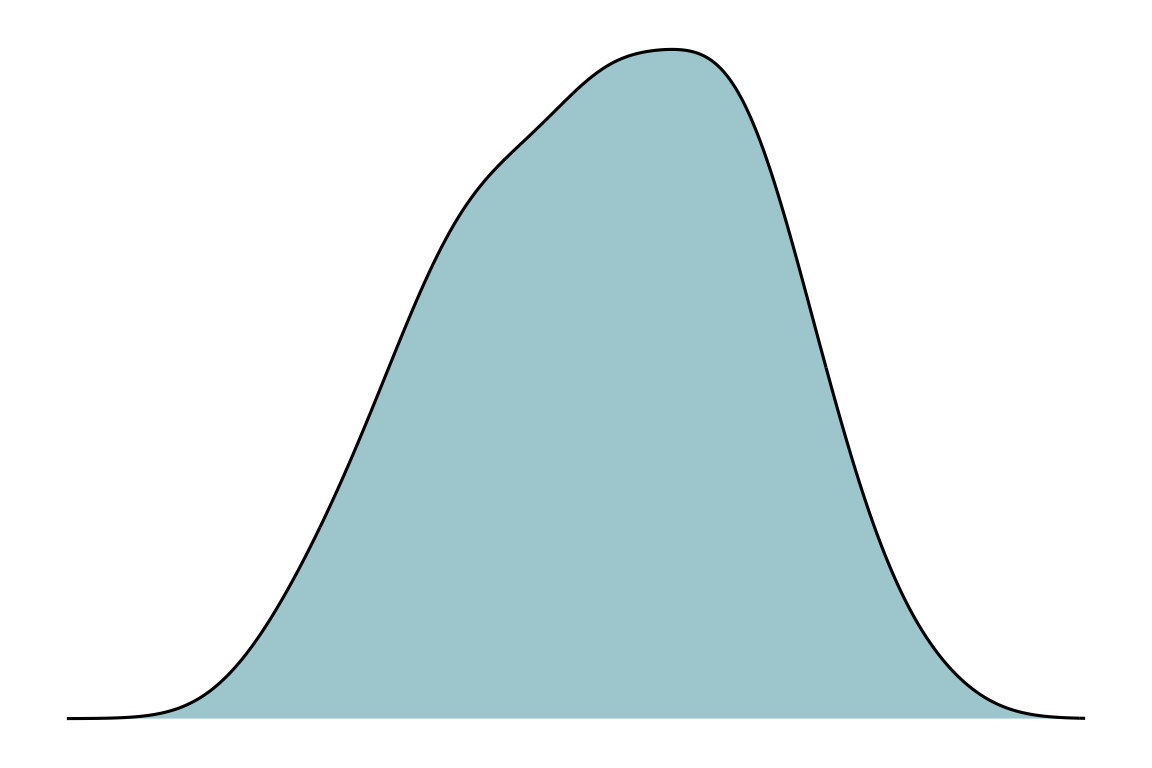
A sűrűségfüggvény azt ábrázolja, hogy milyen valószínűséggel fordulnak elő az adataink. Egész pontosan a görbe alatti területek adják meg a valószínűségeket.
2.3 Centrális tendencia mutatói: középértékek
2.3.1 Átlag
A legismertebb centrális tendencia mutatószám az átlag. Az átlag az összes érték összege osztva az értékek darabszámával.
A populációátlag (amit általában nem ismerünk) képlete: \[ \mu = \frac{\sum_{i=1}^{N}{X_i}}{N} \]
A mintaátlag képlete: \[ M = \bar{X} = \frac{\sum_{i=1}^{n}{X_i}}{n} \]
A publikációkban az átlagot mindig M-mel jelöljük. APA7 formátumban egy vagy két tizedesjegyre kerekítve mutatjuk be (attól függően, hogy a szakfolyóiratnak mik az erre vonatkozó szabályai).
Jellemezzük hát az eloszlásainkat az átlaggal:
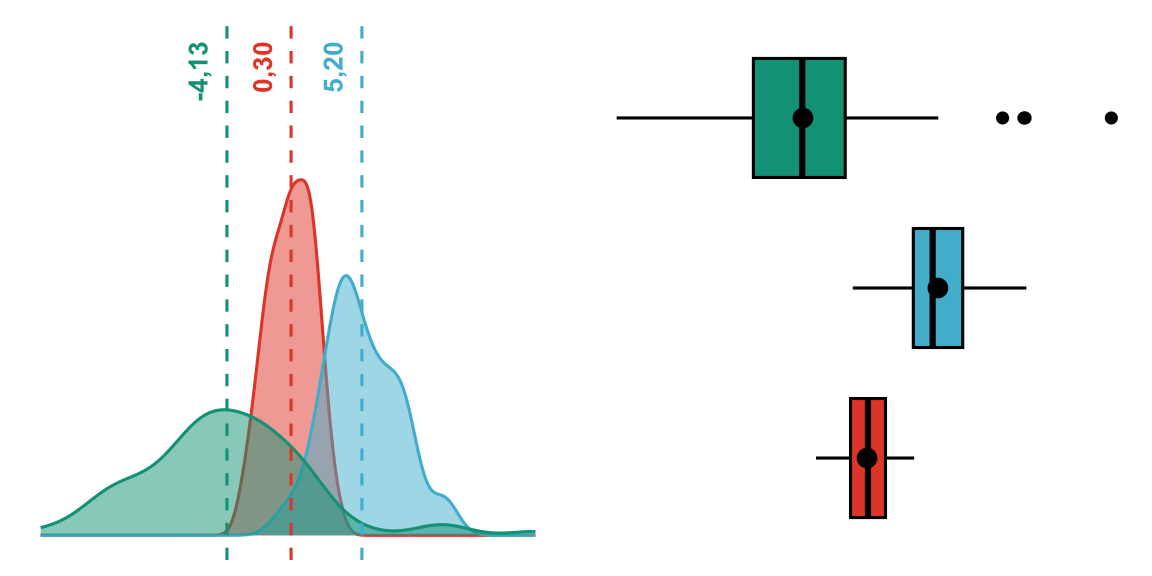
2.3.2 Módusz
A módusz a leggyakoribb érték.
A csupán egy globális módusszal rendelkező eloszlás unimodális. Ilyen például a normál eloszlás is. Ábrázolás során észrevehetjük, hogy egy eloszlásnak lehet globális módusza és lokális módusza is akár (multimodális eloszlás; ha csak két módusza van, akkor bimodálisnak nevezzük).
JASP-ban a nominális és az ordinális mérési szintű változók esetén igaz a definíció. Skála típusú változó esetén a JASP Kernel Density Estimation (kernel sűrűség becslés) módszerrel közelít egy móduszt (ahová az eloszlási görbe csúcsát várja).
2.3.3 Medián
A medián a sorba rendezett adat középső értéke páratlan elemszámú adatsor esetén. Páros számú adatsorban a két középső elem számtani átlaga lesz a medián.
Mediánja ordinális mérési szintű változónak is lehet. Pl. végzettségek esetén a sorba rendezett adatok közül a középső adat végzettségi szintje lesz a medián páratlan elemszám esetén. Páros elemszám esetén nem tudunk átlagolni ordinális változót, így a medián a két egymással határos kategória határán helyezkedik el.
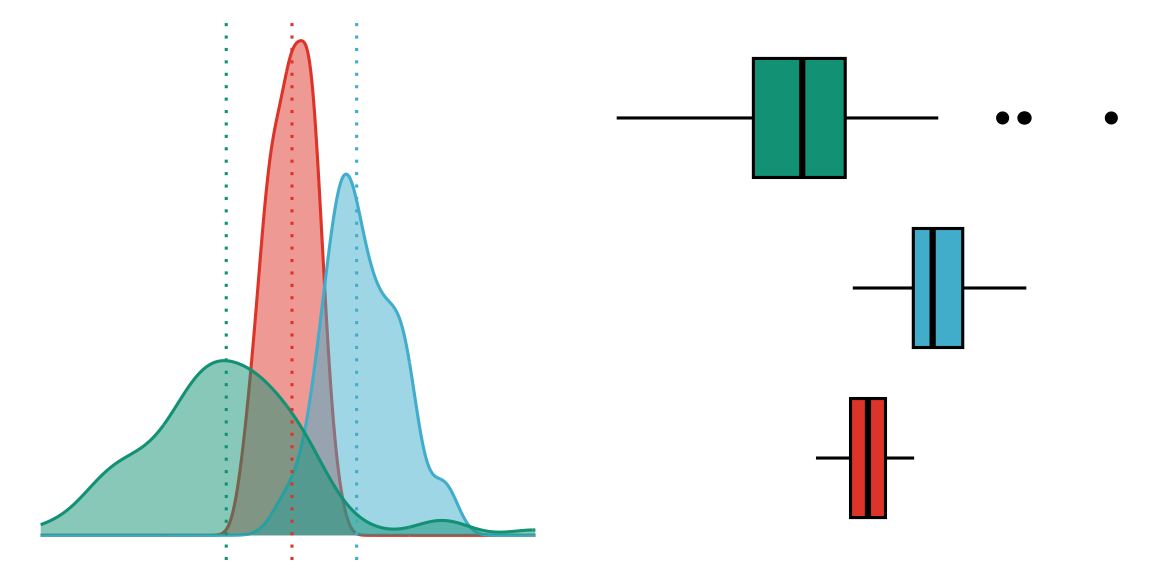
2.4 Szóródásmutatók
2.4.1 Terjedelem
A terjedelem a maximum és minimum értékek különbsége. \[ R = X_{max} - X_{min} \]
2.4.2 Interkvartilis terjedelem
Az interkvartilis terjedelem az adatok 50%-át mutatja, a Q3 és Q1 közötti különbség.
\[ IQR = X_{Q3} - X_{Q1} \]
2.4.3 Átlagos abszolút eltérés
Az adatsor egyes elemeinek az adatsor átlagától való eltérését átlagolva megkapjuk az átlagos abszolút eltérést. Az abszolútértékre azért van szükség, hogy a pozitív és negatív eltérések ne oltsák ki egymást.
A populáció átlagos abszolút eltérése: \[ \delta = \frac{\sum_{i=1}^{N}{|X_i - \mu|}}{N} \]
A minta átlagos abszolút eltérése: \[ D = \frac{\sum_{i=1}^{n}{|X_i - \bar{X}|}}{n} \]
2.4.4 Variancia (szórásnégyzet)
A pozitív és negatív eltérések kioltásának elkerülésére szintén alkalmas a különbségek négyzetre emelése abszolút érték helyett.
Definíció 2.1 A variancia az átlagtól vett eltérések négyzetes átlaga. Azt mutatja meg, hogy a minta mért értékei átlagosan milyen messze helyezkednek el a minta számtani átlagától négyzetes egységben.
A populáció varianciája: \[ \sigma^2 = \frac{\sum_{i=1}^{N}{(X_i - \mu)^2}}{N} \]
A minta varianciája: \[ s^2 = \frac{\sum_{i=1}^{n}{(X_i - \bar{X})^2}}{n-1} \]
Láthatjuk, hogy a minta varianciája esetén nem a teljes elemszámmal, hanem \(n-1\) értékkel osztunk. Ez az úgynevezett Bessel-korrekció.
2.4.4.1 Bessel-korrekció
A mintánk átlaga és a populáció átlaga nagy valószínűséggel eltér. A minta átlaga körüli variancia kisebb, mint a populáció átlaga körüli variancia, függetlenül attól, hogy a minta átlaga kisebb vagy nagyobb a populáció átlagánál. Vagyis a minta varianciája korrekció nélkül mindig alábecsüli a populáció varianciát. Ráadásul a mintánkat a mintaátlag jobban jellemzi, mint a populációátlag (és a populációátlag a gyakorlatban nem ismert).
Szabadságfok-megközelítés alapján: A mintaátlag mint becslés, már „elhasznált” egy szabadságfokot a közelítésben, már csak n-1 adatpont variálható szabadon.
2.4.5 Szórás (standard deviation)
A variancia önmagában nehezen értelmezhető a négyzetösszeg miatt, ezért a szórást szoktuk a gyakorlatban használni (például a demográfiai adatokat átlag és szórás kombinációjában mutatjuk be).
Definíció 2.2 A szórás a variancia négyzetgyöke. A minta pontjainak átlagos távolsága a minta átlagától az eredeti mértékegységben kifejezve.
A populáció szórása: \[ \sigma = \sqrt{\frac{\sum_{i=1}^{N}{(X_i - \mu)^2}}{N}} \]
A minta szórása (SD): \[ s = \sqrt{\frac{\sum_{i=1}^{n}{(X_i - \bar{X})^2}}{n-1}} \]
2.5 Eloszlás alakja
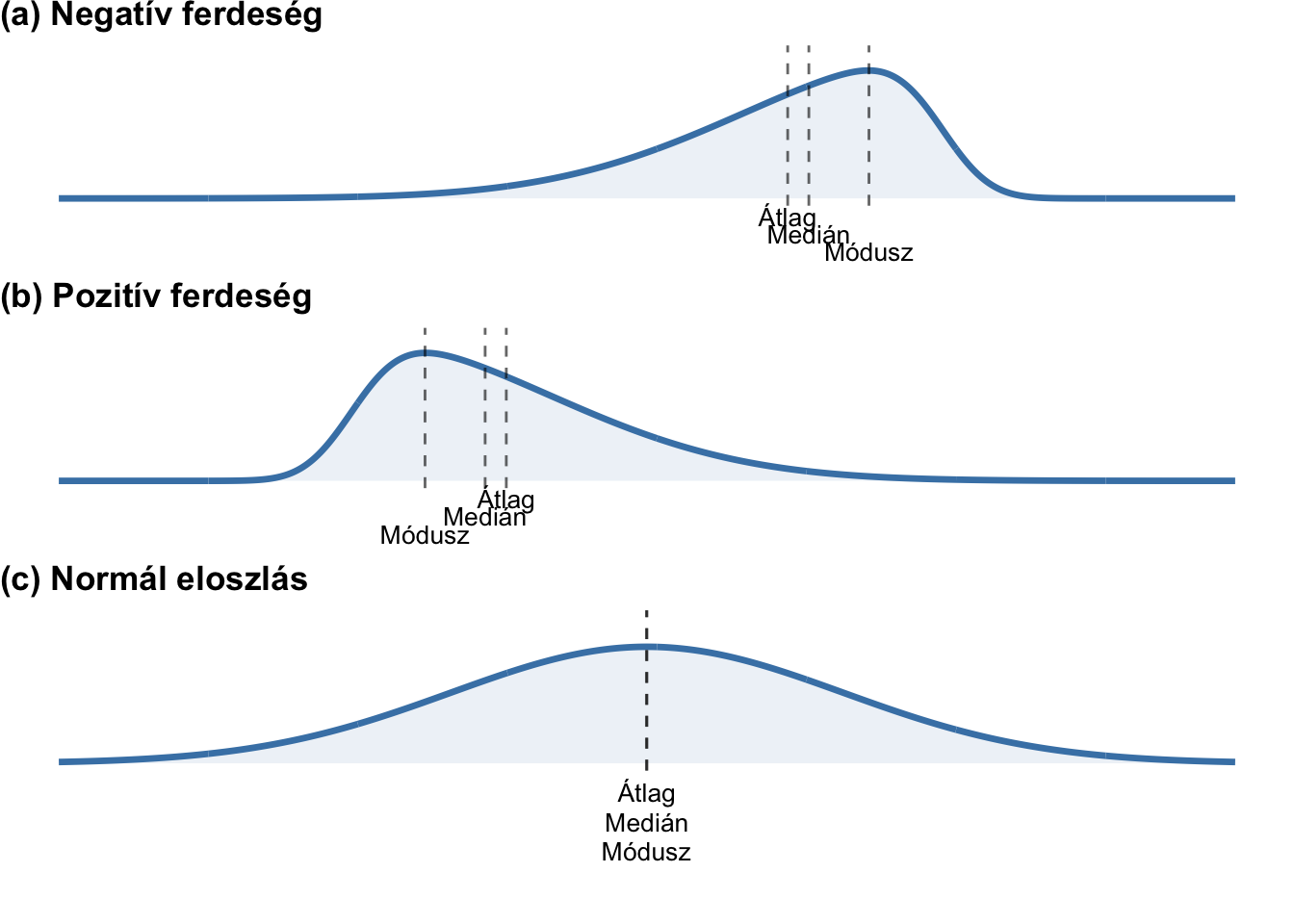
2.5.1 Ferdeség (skewness)
Az eloszlás középérték körüli aszimmetriájának mértékét jelzi.
\[ skew(X) = \frac{\sum_{i=1}^{n}{(X_i - \bar{X})^3}}{n \times s^3} \]
A ferdeség mutatói:
- A negatív ferdeség balra ferdeséget jelent, mert az eloszlás „farka” bal oldalra, az alacsonyabb értékek felé nyúlik el.
- A pozitív ferdeség jobbra ferdeséget jelent, mert az eloszlás „farka” jobb oldalra, a magasabb értékek felé nyúlik el.
- Normál eloszlás esetén a ferdeség 0.
2.5.2 Csúcsosság (kurtosis)
Az eloszlás vertikális alakját leíró mutatószám az (excess) kurtosis. A normál eloszlás excess csúcsossága nulla (sima csúcsossága 3, de nem azzal dolgozunk). Pozitív érték esetén az eloszlás csúcsos, negatív érték esetén pedig lapos.
\[ excess\ kurtosis = K_e = \frac{\sum_{i=1}^{n}{(X_i - \bar{X})^4}}{n \times s^4} -3 \]
A csúcsosság típusai:
- mezokurtikus, amikor Ke = 0: normáleloszlás
- leptokurtikus, amikor Ke > 0: csúcsosabb, nehezebb farkakkal (pl. t-eloszlás)
- platikurtikus, amikor Ke < 0: laposabb, könyebb farkakkal (pl. béta-eloszlás)
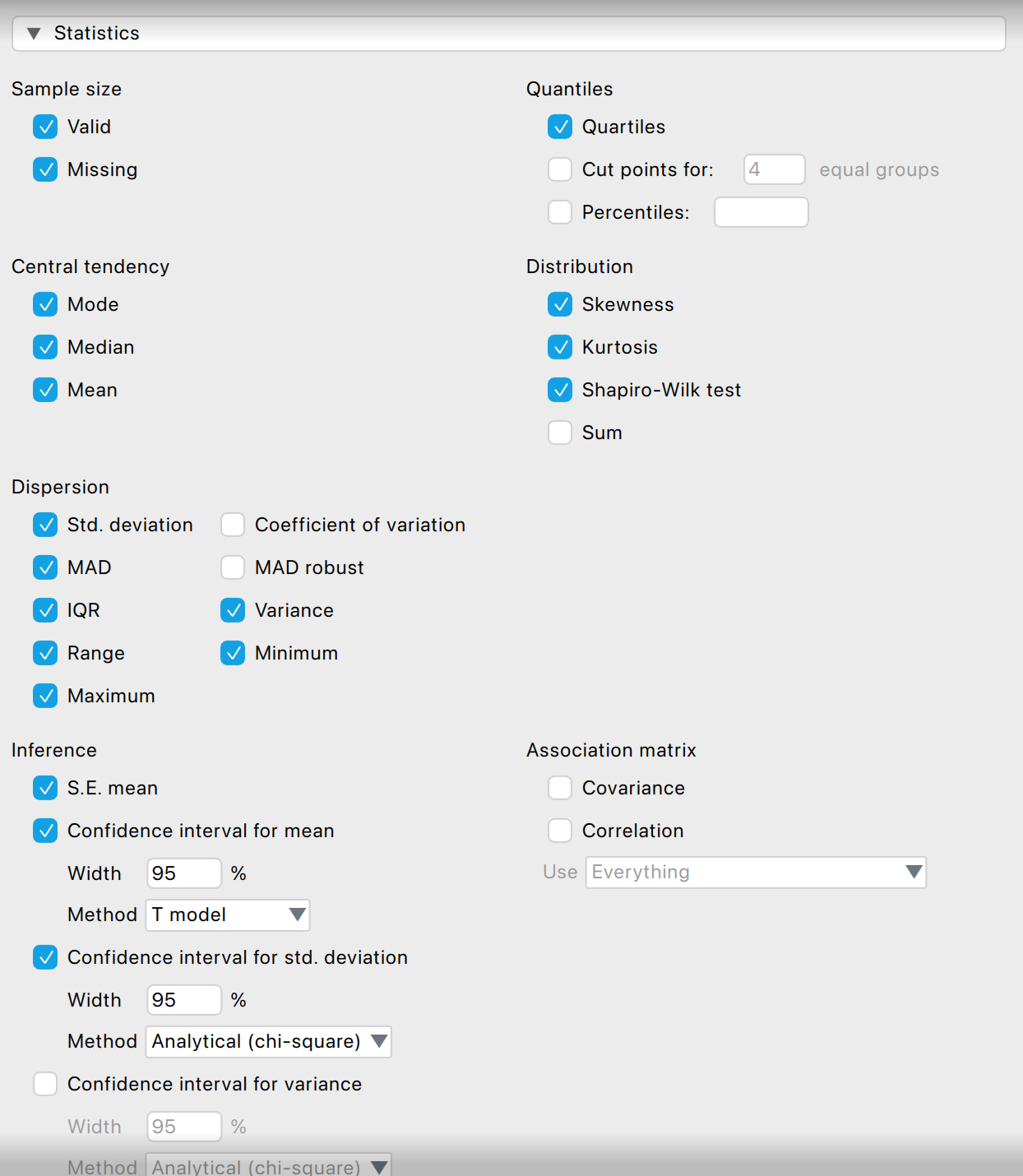
2.6 Leíró statisztikai mutatók kiszámítása JASP-ban
JASP-ban egyszerűen ki tudjuk számítani az összes bemutatott (és annál több) leíró statisztikai mutatót a Descriptive Statistics modul Statistics rovatában.