13 Egyszempontos varianciaanalízisek (one-way ANOVA)
13.1 Szempontok. Függetlenség.
Az egyszempontos varianciaanalízis (one-way ANOVA) során csupán egy szempont szerint szeretnénk szegmentálni az adatainkat. Ez az egy szempont például a végzettségi szint, vagy különféle antidepresszáns hatóanyagai, vagy terápiás módozatok stb. A szempont több, mint 2 csoportot tartalmaz.
Mi a szempont? A végzettségi szint mint szempontunk például 3 db csoportot (pl. alap-, közép-, felsőfokú) tartalmazhat, vagy akár 5 db csoportot (pl. alapfok, középfok, főiskola, egyetem, PhD). Terápiás módozatok esetén például az általunk vizsgált 4 módozatot: kognitív viselkedésterápia, pszichodinamikus terápia, pszichodráma, sématerápia.
Az egyszempontos ANOVA lényege, hogy csak az egyik szempont szerinti szegmentálást vesszük bele a vizsgálatba: vagy csak a végzettségi szintet vagy csak a terápiás módozatot.
A többszempontos ANOVA során a vizsgált változónkat több szempont szerint is tudjuk majd szegmentálni (tehát végzettségi szint és terápiás módozat szerint), de ilyenkor a szempontok interaktálhatnak egymással. Ez a többváltozós statisztika területe, ami mesterszakos tananyag a pszichológiai képzésekben.
Függetlenség tekintetében (ahogy t-próbánál is) megkülönböztetünk függetlenmintás ANOVA-t, ezt általában egyszerűen egyszempontos varianciaanalízisnek (one-way ANOVA) hívjuk, bővebb nevén egyszempontos függetlenmintás varianciaanalízisnek. Ilyen például: terápiás módozatok összehasonlítása.
Az összefüggő mintás elrendezés (mivel általában ismételt mérés eredménye) gyakran egyszempontos ismételt méréses varianciaanalízisnek (one-way repeat measures ANOVA), vagy egyszempontos összefüggő mintás varianciaanalízisnek is hívhatjuk. Például: terápiás intervenció előtt–közben–után elrendezés.
13.2 Az egyszempontos varianciaanalízis (one-way ANOVA) feltételei
Ahogy azt már megszokhattuk, a hipotézistesztelésünk során bizonyos jellemzők meglétét feltételezzük, így hát az egyszempontos varianciaanalízisnak is vannak feltételei:
A vizsgált személyek függetlenek egymástól
Hasonlóan a függetlenmintás t-próbához, feltételezzük, hogy egyik alany válasza a kérdőíves vizsgálaton nem befolyásolja a másik alanyunk válaszát. A személyek/mintaelemek függetlenek. Ezt a kísérleti elrendezésünk kell biztosítsa.
A csoportok függetlenek egymástól
Azt feltételezzük, hogy az összehasonlítandó csoporttagságok kölcsönösen kizárják egymást (pl. nem lehet valaki egyszerre alapfokú és felsőfokú végzettségűként besorolva). A független változó faktorszintjei disztinkt halmazok. Ezt a kísérleti elrendezésünk kell biztosítsa.
A függő változó skála típusú
A függő változó (amiben vizsgáljuk a különbségeket) legalább intervallumskála (így kezeljük a Likert kérdőív pontszámait is) mérési szintű. Erről magunk kell meggyőződjünk.
Ordinális mérési szintű változó esetén nemparaméteres alternatívát (Kruskal-Wallis teszt) választuk majd. Ha a függő változó bináris, akkor logisztikus regressziót vagy χ2 próbát alkalmazzunk inkább!
Nincsenek többdimenziós outlierek
Ez nem alapfeltétel, de megbízhatóbb a próbánk eredményének értelmezése, ha ez fennáll.
Egyszempontos és faktoriális varianciaanalízis esetén az egydimenziós outliereket teszteljük például IQR módszerrel, szükség esetén winsorizálással.
A többdimenziós outlierek esetén a befolyásos és torzító értékek számítanak, amit Cook-féle távolsággal tudunk ellenőrizni (többféle kritériumszint mellett, legmegengedőbb: Cook D < 1). Ezt a vizsgálatot a Linear Regression modul tartalmazza, az ANOVA nem.
A függő változó csoportonként normál eloszlású
Ha minden összehasonlítandó csoport elég nagy, akkor a leíró statisztikai modulban a Split segítségével meg tudjuk vizsgálni a függő változó normál eloszlását a Shapiro–Wilk próbával. Ennél fontosabb feltétel azonban a reziduumok normál eloszlása.
Ha a csoportonkénti Shapiro-Wilk próba szignifikáns (tehát p < 0,05 és így nem teljesül a normál eloszlás feltétele), elvégezhetjük a varianciaanalízist, ha:
- a csoportok elemszáma hasonló (< 30% a különbség a legnagyobb és legkisebb csoport elemszáma között)
- csoportonként legalább n > 15 az elemszám
- teljesül a szóráshomogenitás
A modell hibatagjai (reziduumok, reziduálisok) normál eloszlást követnek
A modell reziduálisainak normál eloszlását kétféleképpen tudjuk ellenőrizni a JASP protokollban.
Egyrészt a standardizált reziduálisok Q-Q plotját tudjuk ellenőrizni (mintázat nélkül, a vörös átló mentén helyezkedjenek el az ábrázolt pontok)
Másrészt a standardizált reziduálisokat exportálni tudjuk önálló oszlopként, és ezen tudunk Shapiro-Wilk próbát futtatni.
Fennáll a csoportonkénti szóráshomogenitás
A JASP ANOVA moduljában található Assumption Checks szekcióban a Homogeneity tests funkció tartalmazza: a Levene-próba áll rendelkezésünkre. (Nem áll itt rendelkezésre Brown–Forsythe-próba.) Azt várjuk, hogy a Levene-próba eredménye ne legyen szignifikáns (vagyis p > 0,05 legyen), mert ez esetben feltételezhetjük, hogy fennáll a szóráshomogenitás az összehasonlítandó csoportok között.
Ha sérül a szóráshomogenitás, a vizsgálat még elvégezhető, ha:
- a csoportok elemszáma hasonló (< 30% a különbség a legnagyobb és legkisebb csoport elemszáma között)
- és a legkisebb és legnagyobb varianciák aránya \(\frac{{VAR}_{max}}{{VAR}_{min}}<4\)
- VAGY ha egyik feltétel sem teljesül, de mégis a kisebb csoporthoz tartozik a kisebb variancia, a nagyobbhoz a nagyobb variancia, akkor korlátozottan értelmezhetjük az ereményeket
Ha a szóráshomogenitás feltétele nem teljesül (Levene-próba szignifikáns, p < 0,05), akkor a JASP képes homogenitás-korrekciókra is:
– ANOVA tábla korrekciójára Brown–Forsythe vagy Welch korrekciók alkalmazhatók, ilyenkor a megfelelő korrigált értéket kell kiolvasni az ANOVA táblából. Nagyon leegyszerűsítve a Brown–Forsythe-féle korrekciót főleg kis elemszámú, nagy ferdeségű, sok extrém értéket tartalmazó, nem illesztett minta esetén használunk, más esetben használjuk a Welch korrekciót!
- a post-hoc teszt korrekciójára Games–Howell post-hoc korrekciót alkalmazunk JASP-ban. (A Dunnett próba itt nem a Dunnett T3-féle korrekciót jelöli.)
13.2.1 Az egyszempontos ANOVA tábla értelmezése
Sematikus felépítése a következő:
| Modell | Sum of squares | df | Mean Square | F | p |
|---|---|---|---|---|---|
| Szempont neve (Between groups) | SSM: Sum of squares of model | dfM = k - 1 | MSM = SSM / dfM | F = MSM / MSR | p |
| Residuals (Within groups) | SSR: Sum of squared residuals | dfR = n - k | MSR = SSR / dfR | ||
| Total | SST: Sum of squares total | dfT = n -1 |
Észrevehetjük, hogy az F-értékhez eljutás során a különféle négyzetösszegeket arányosítjuk a szabadságfokokkal és megállapítjuk az F értéket.
A p-érték meghatározása az F-eloszlás kritikus értékén alapul. Az F-statisztikánknak két szabadságfoka van, a dfM és dfR. Tehát megkeressük, hogy milyen valószínűséggel fordul elő az F-statisztikánk értéke egy F(dfM, dfR) eloszláson.
13.3 Példák egyszempontos varianciaanalízisre
Példa 13.1 (Példa egyszempontos varianciaanalízisre (szóráshomogenitás feltétele teljesül)) Klinikánkon depresszióval diagnosztizált klienseket három csoportra osztva, háromféle terápiás módozatban kezeltük: i) alacsony intenzitású intervenciókkal, ii) kognitív viselkedésterápiával (CBT), valamint iii) sématerápiával. Az intervenciók hosszában nem volt különbség. Az intervenciók előtti depressziós állapotot nem vettük figyelembe. Kíváncsiak vagyunk, hogy melyik volt a hatékonyabb eljárás. Előfeltételezésünk nincs.
Az adatsor itt letölthető: modalitas.sav
A megoldás lépéseihez pár kulcsszó:
- varianciaanalízist végzünk, nem pedig t-próbát, mert három csoportot/módozatot tesztelünk
- mindenki egy csoportba tartozik csak, tehát függetlenek
- az intervenciók hosszában nem volt különbség, így azt mint extra szempontot nem kell most figyelembe vegyük
- a kezelések előtti állapotot nem mértük, tehát nem ismételt méréses elrendezést használunk
- magasabb depresszió pontszámot alacsonyabb sikerességnek értékelünk
- nincs konkrét feltételezésünk egy kimondott modalitásról, hanem összehasonlítani szeretnénk őket, ezért szignifikáns F-próba esetén post-hoc tesztet végzünk, nem pedig kontrasztvizsgálatot.
Állítsuk be a próbát a JASP-ban, de ne olvassuk le még az eredményeket:
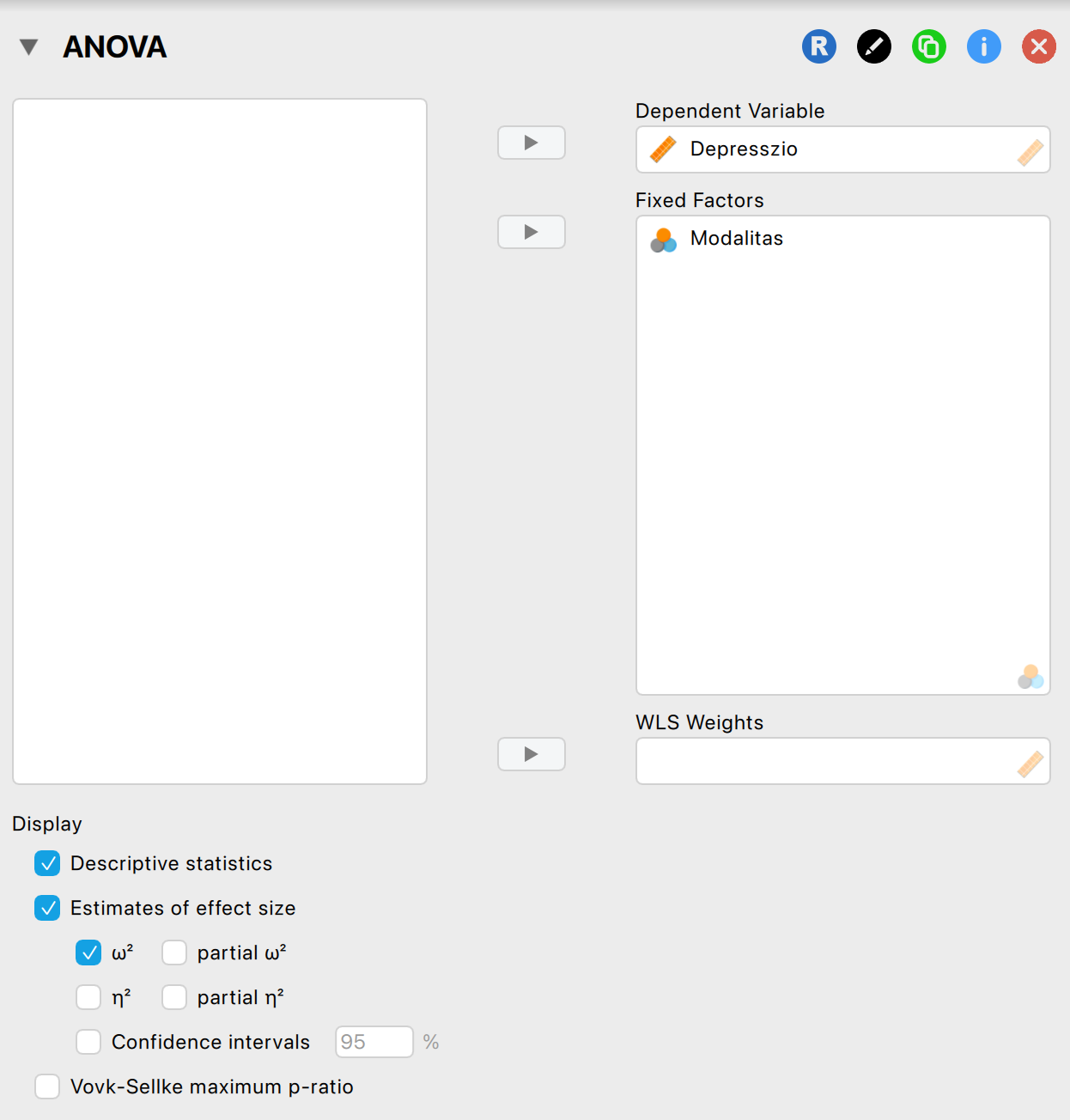
Nézzük meg, hogy teljesülnek-e a feltételek:
A személyek függetlenek
A csoportok függetlenek: mindenki csak egy csoportban/módozatban vett részt
A depresszió pontszám skála típusú
Többdimenziós outliert jelenleg nem vizsgálunk JASP-ban. (A lineáris regressziós modulban ez rendelkezésre áll pl. Cook-féle távolság.) De egydimenziós outlierek nincsenek, ezt boxplottal ellenőrizhetjük.
A csoportonkénti normál eloszlás a gyengébb feltétel, de elvégezhetjük a leíró statisztikai modulban. Láthatjuk, hogy a depresszió pontszám az alacsony intervenció és sématerápia csoportokban normál eloszlást követ, de a CBT csoportban nem. A csoportok elemszáma viszont tökéletesen megegyezik és kellő nagyságú.
A reziduumok normál eloszlását is megvizsgáljuk, ez az erősebb normalitásfeltétel. Ezt a Q-Q plot of residuals funkcióval vizsgáljuk. Láthatjuk, hogy szabályosan követik a pontok az átlót.
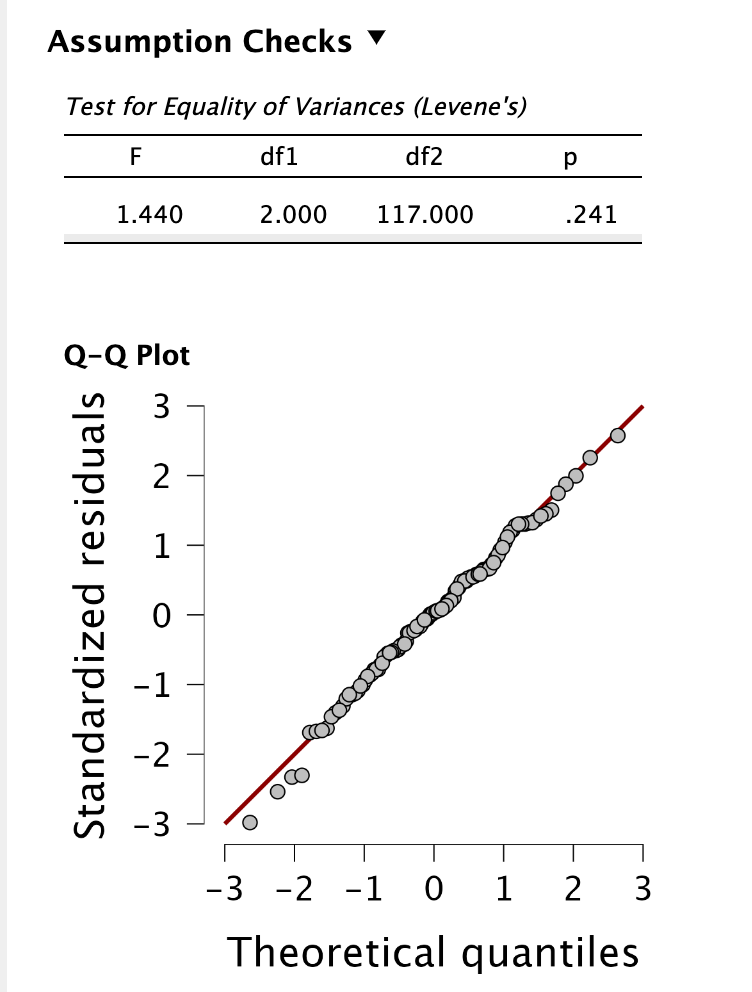
A szóráshomogenitást a Homogeneity tests funkcióval vizsgáljuk, ahol egy Levene-próbát kapunk eredményül. Láthatjuk, hogy mivel nem szignifikáns (p > 0,05), ezért a szóráshomogenitás feltétele teljesül. Homogenitáskorrekciót nem kell alkalmaznunk.
ANOVA tábla leolvasása:
A feltételvizsgálatok ellenőrzését követően leolvassuk az ANOVA táblánkban szereplő értékeket. Ha kipipáltuk a Descriptive statistics funkciót, akkor a szöveges eredményközléshez szükséges leíró statisztikai mutatók is rendelkezésünkre állnak:
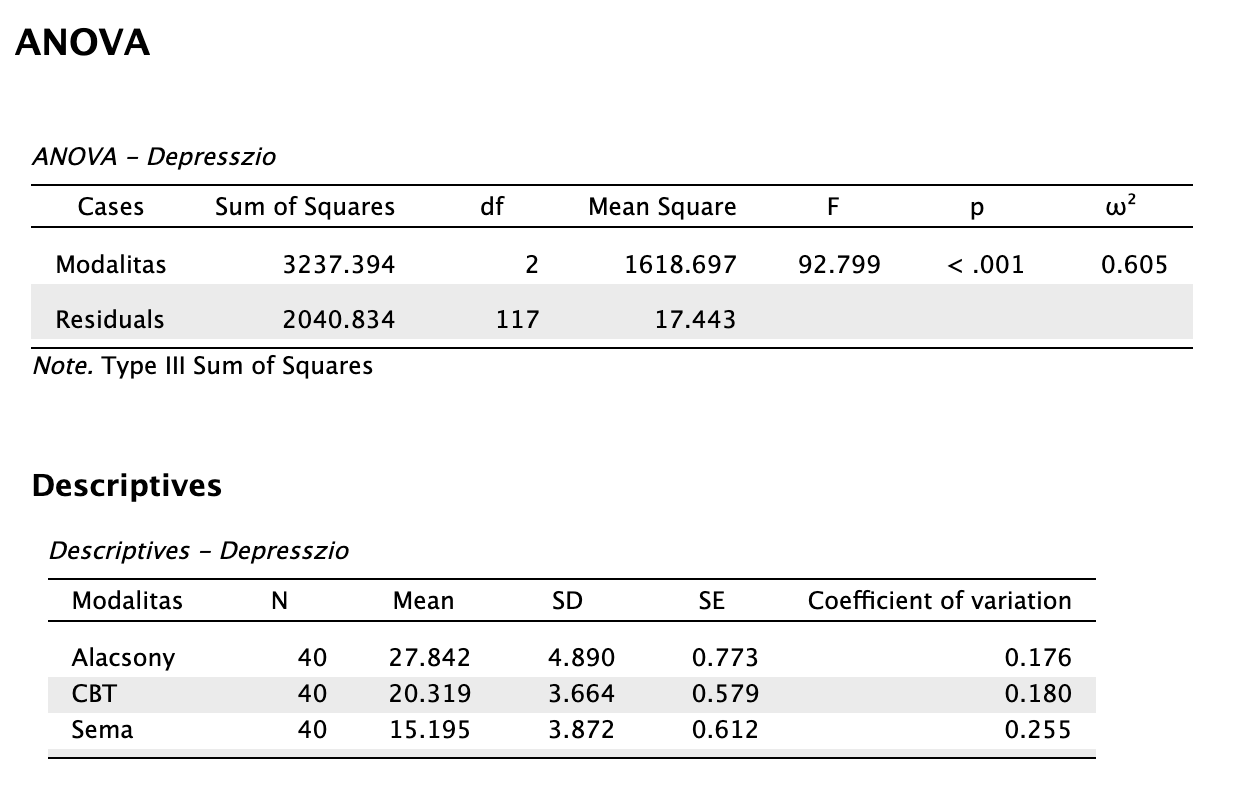
Vegyük észre első lépésben, hogy az omnibus F-próbánk eredménye szignifikáns, tehát a csoportok között van különbség. Az ómeganégyzet mint hatásnagyságmutató meg is mutatja nekünk, hogy nagy hatásról van szó.
A leíró statisztikai mutatók között áz átlagok összehasonlításával „szemre” is láthatjuk, hogy viszonylag nagy különbségek vannak az átlagok között. Ezt ábrázolni is tudjuk többféle grafikonnal (Descriptives Plots, Bar Plots, Raincloud Plots). Ezek közül az eloszlásokat is a Raincloud Plots tartalmazza:
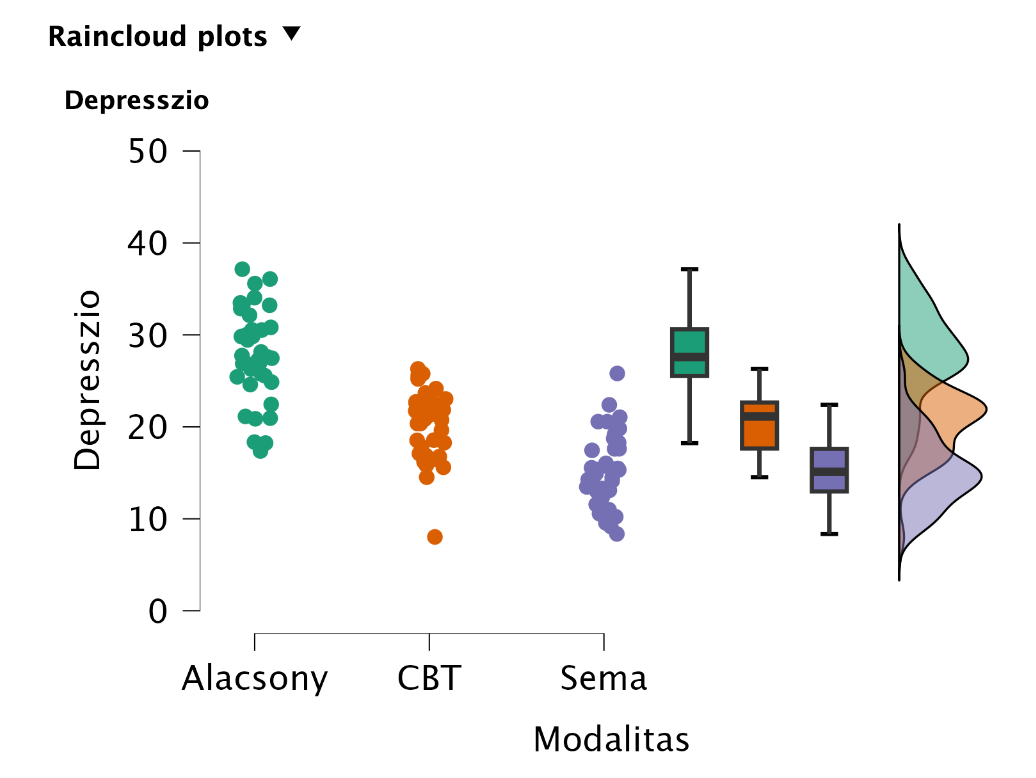
Post-hoc teszt:
Mivel az omnibus F-próba szignifikáns eredményű, és nem volt konkrét erős feltételezésünk, post-hoc tesztet végzünk, hogy exploráljuk a különbségeket.
A beállításokat az alábbiak szerint végezzük el:
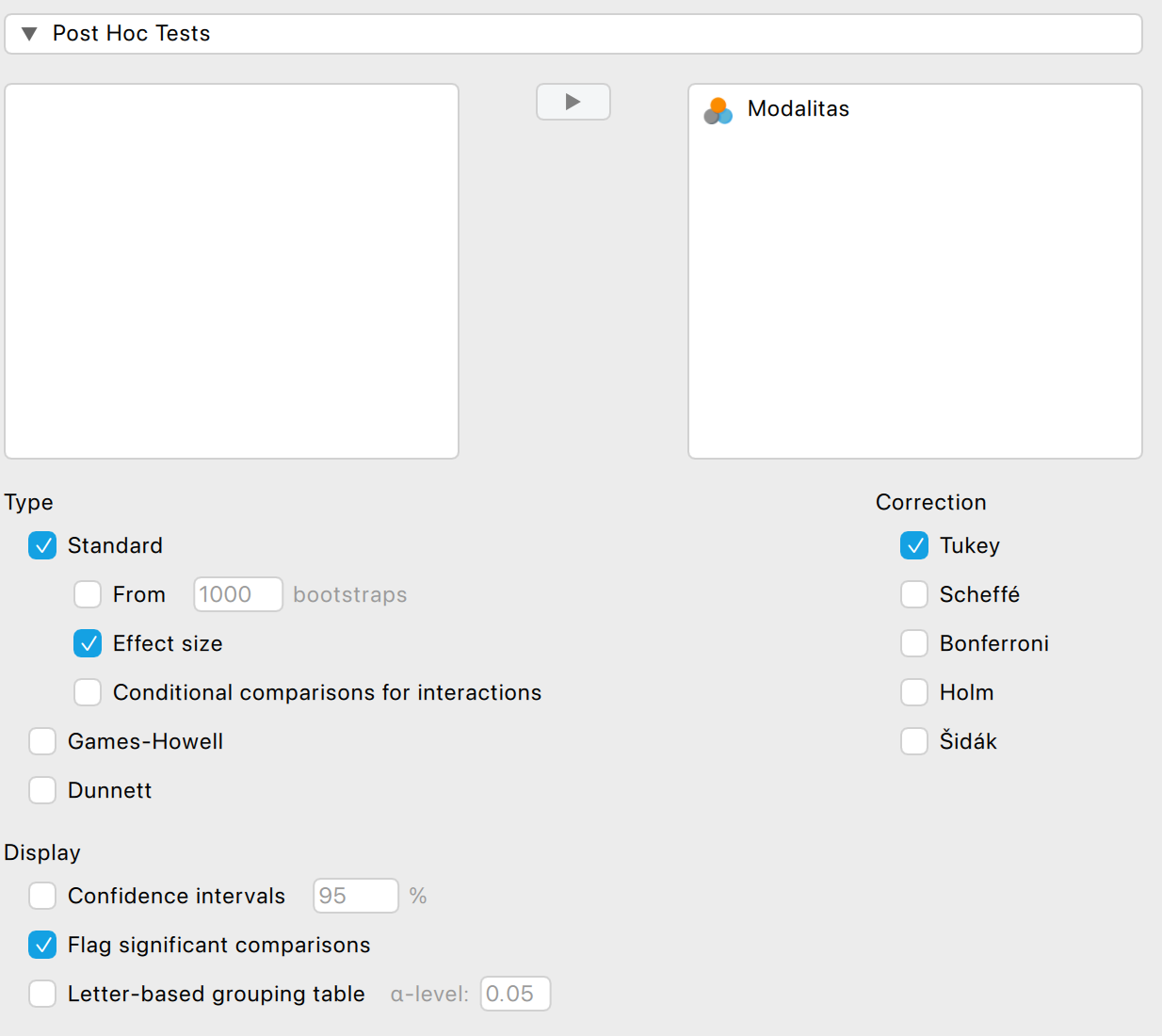
- Az Effect size rovatot feltétlenül kipipáljuk, ha nem lenne alapból kipipálva
- Tukey-féle korrekciót használunk, mert nem sérülnek az ANOVA feltételei, fennáll a szóráshomogenitás, azonos méretűek a csoportok és nem ismételt méréses vizsgálatot végzünk.
Leolvassuk a post-hoc teszt eredményeit:
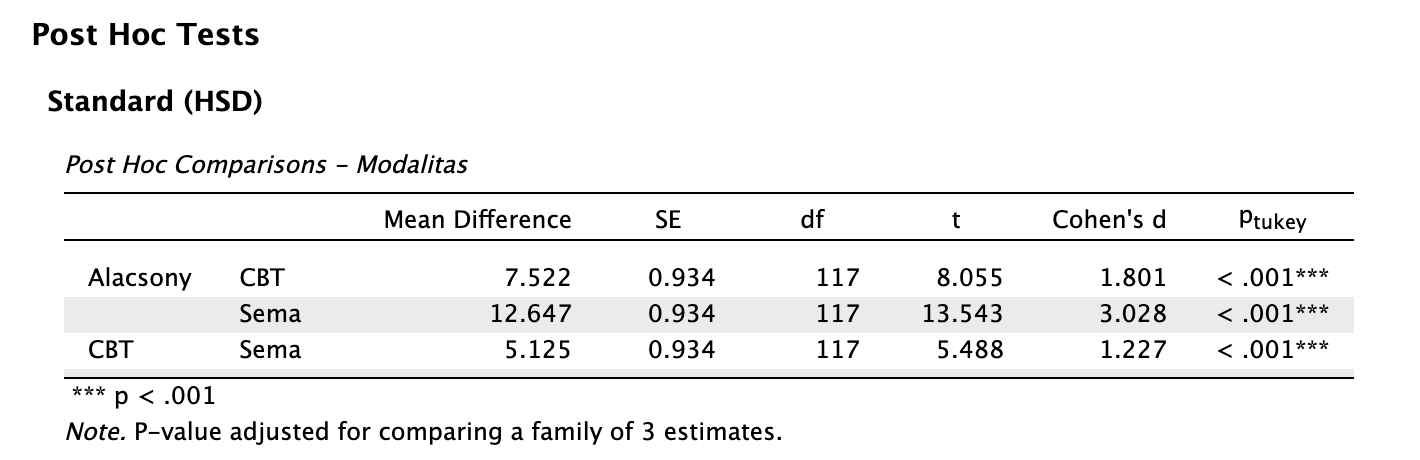
Láthatjuk, hogy mindegyik összehasonlításban szignifikánsak az eredmények (mert ptukey < 0,05), és nagy Cohen-d hatásnagyságokat láthatunk.
Megoldás 13.1. [Módszerek részben:] A terápiás modalitások összehasonlítására egyszemponos varianciaanalízist (one-way ANOVA) végeztünk. Mivel az éta-négyzet túlbecsüli a hatásnagyságot, az ómega-négyzetet alkalmaztuk az omnibus próba esetén, ami különösen indokolt kis-közepes minták esetén. A post-hoc tesztek során a VA feltételeinek teljesülése esetén Tukey-féle, nem teljesülése esetén Scheffé-féle korrekciót alkalmaztunk.
[Eredmények részben:]1
A terápiás modalitások összehasonlítására végzett egyszemponos VA feltételvizsgálatai alapján a maradványértékek normál eloszlást követtek a QQ plot szemrevételezése alapján, és fennállt a csoportok között a szóráshomogenitás a Levene-próba eredménye szerint: F(2, 117) = 1,440, p = 0,241.
A modalitások közötti összkülönbség statisztikailag szignifikáns volt nagy hatásnagysággal: F(2, 117) = 92,799, p < 0,001, ω2 = 0,605. Az egyes csoportokra vonatkozó utóvizsgálatok eredménye szerint az alacsony intenzitású csoportnál mért átlagos depressziópontszám (M = 27,84, SD = 4,89) nagy hatásnagysággal statisztikailag szignifikánsan magasabb mind a CBT (M = 20,32, SD = 3,66; t(117) = 8,055, ptukey < 0,001, d = 1,801), mind a sématerápiás csoport átlagánál (M = 15,20, SD = 3,87; t(117) = 13,543, ptukey < 0,001, d = 3,028). Továbbá szintén nagy hatásnagyságú, statisztikailag szignifikáns különbséget találtunk a sématerápia és kognitív viselkedésterápia között is a sématerápia javára: t(117) = 5,488, ptukey < 0,001, d = 1,227.
[Diszkusszióban értelmezzük, miszerint a sématerápiát gondoljuk hatékonyabbnak a három modalitás közül – ennek a következtetésnek a limitációival együtt.]
Példa 13.2 (Példa egyszempontos varianciaanalízisre (szóráshomogenitás feltétele nem teljesül)) Klinikánkon depresszióval diagnosztizált klienseket három csoportra osztva, háromféle terápiás módozatban kezeltük: i) alacsony intenzitású intervenciókkal, ii) kognitív viselkedésterápiával (CBT), valamint iii) sématerápiával. Az intervenciók hosszában nem volt különbség. Az intervenciók előtti depressziós állapotot nem vettük figyelembe. Kíváncsiak vagyunk, hogy melyik volt a hatékonyabb eljárás. Előfeltételezésünk nincs.
Az adatsor itt letölthető: modalitas_sigLev.sav
A megoldás lépéseihez pár kulcsszó:
- varianciaanalízist végzünk, nem pedig t-próbát, mert három csoportot/módozatot tesztelünk
- mindenki egy csoportba tartozik csak, tehát függetlenek
- az intervenciók hosszában nem volt különbség, így azt mint extra szempontot nem kell most figyelembe vegyük
- a kezelések előtti állapotot nem mértük, tehát nem ismételt méréses elrendezést használunk
- magasabb depresszió pontszámot alacsonyabb sikerességnek értékelünk
- nincs konkrét feltételezésünk egy kimondott modalitásról, hanem összehasonlítani szeretnénk őket, ezért szignifikáns F-próba esetén post-hoc tesztet végzünk, nem pedig kontrasztvizsgálatot.
Állítsuk be a próbát a JASP-ban, de ne olvassuk le még az eredményeket:

Nézzük meg, hogy teljesülnek-e a feltételek:

A személyek függetlenek
A csoportok függetlenek: mindenki csak egy csoportban/módozatban vett részt
A depresszió pontszám skála típusú
Többdimenziós outliert jelenleg nem vizsgálunk JASP-ban. (A lineáris regressziós modulban ez rendelkezésre áll pl. Cook-féle távolság.) De egydimenziós outlierek nincsenek, ezt boxplottal ellenőrizhetjük.
A csoportonkénti normál eloszlás a gyengébb feltétel, de elvégezhetjük a leíró statisztikai modulban. Láthatjuk, hogy a depresszió pontszám az alacsony intervenció és sématerápia csoportokban normál eloszlást követ, de a CBT csoportban nem. A csoportok elemszáma viszont tökéletesen megegyezik és kellő nagyságú.
A reziduumok normál eloszlását is megvizsgáljuk, ez az erősebb normalitásfeltétel. Ezt a Q-Q plot of residuals funkcióval vizsgáljuk. Láthatjuk, hogy szabályosan követik a pontok az átlót.
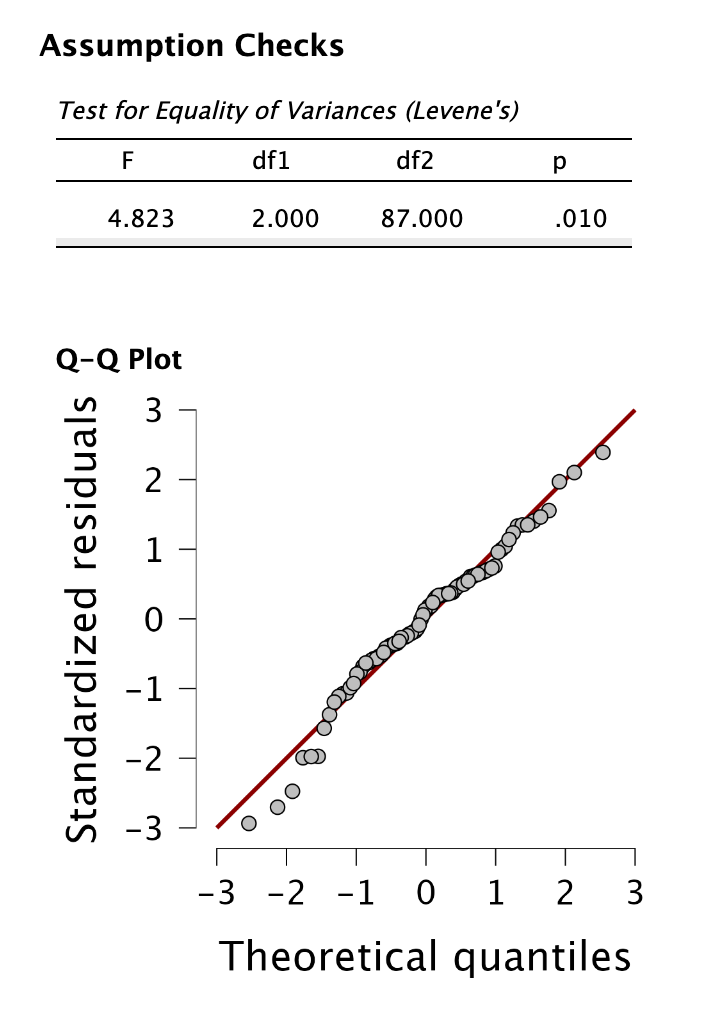
A szóráshomogenitást a Homogeneity tests funkcióval vizsgáljuk, ahol egy Levene-próbát kapunk eredményül. Láthatjuk, hogy a próba eredménye szignifikáns (p < 0,05, mert p = 0,010), ezért a szóráshomogenitás feltétele nem teljesül. Homogenitáskorrekciót kell alkalmaznunk. Mivel illesztett mintáról beszélhetünk és nincs extrém ferdeség az adatokban, a Welch-féle homogenitáskorrekciót alkalmazzuk.
ANOVA tábla leolvasása:
A feltételvizsgálatok ellenőrzését követően leolvassuk az ANOVA táblánkban szereplő értékeket. Ezek közül kiemelten fontos, hogy csak a Welch homonegitáskorrekcióval jelölt eredményeket olvassuk le!
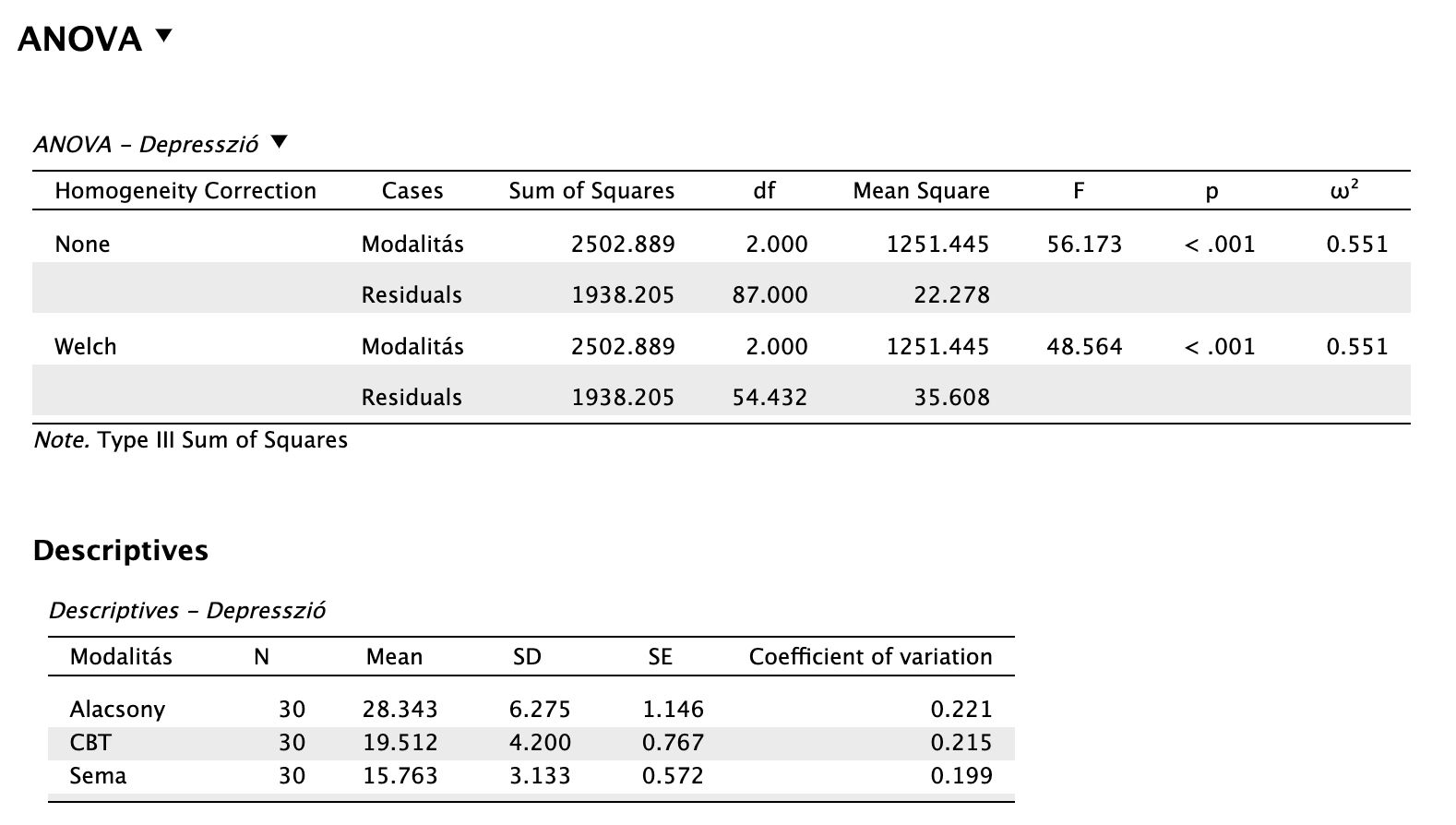
Vegyük észre első lépésben, hogy az omnibus F-próbánk eredménye szignifikáns, tehát a csoportok között van különbség. Az ómeganégyzet mint hatásnagyságmutató meg is mutatja nekünk, hogy nagy hatásról van szó.
A leíró statisztikai mutatók között áz átlagok összehasonlításával „szemre” is láthatjuk, hogy viszonylag nagy különbségek vannak az átlagok között. Ezt ábrázolni is tudjuk többféle grafikonnal (Descriptives Plots, Bar Plots, Raincloud Plots). Ezek közül az eloszlásokat is a Raincloud Plots tartalmazza:
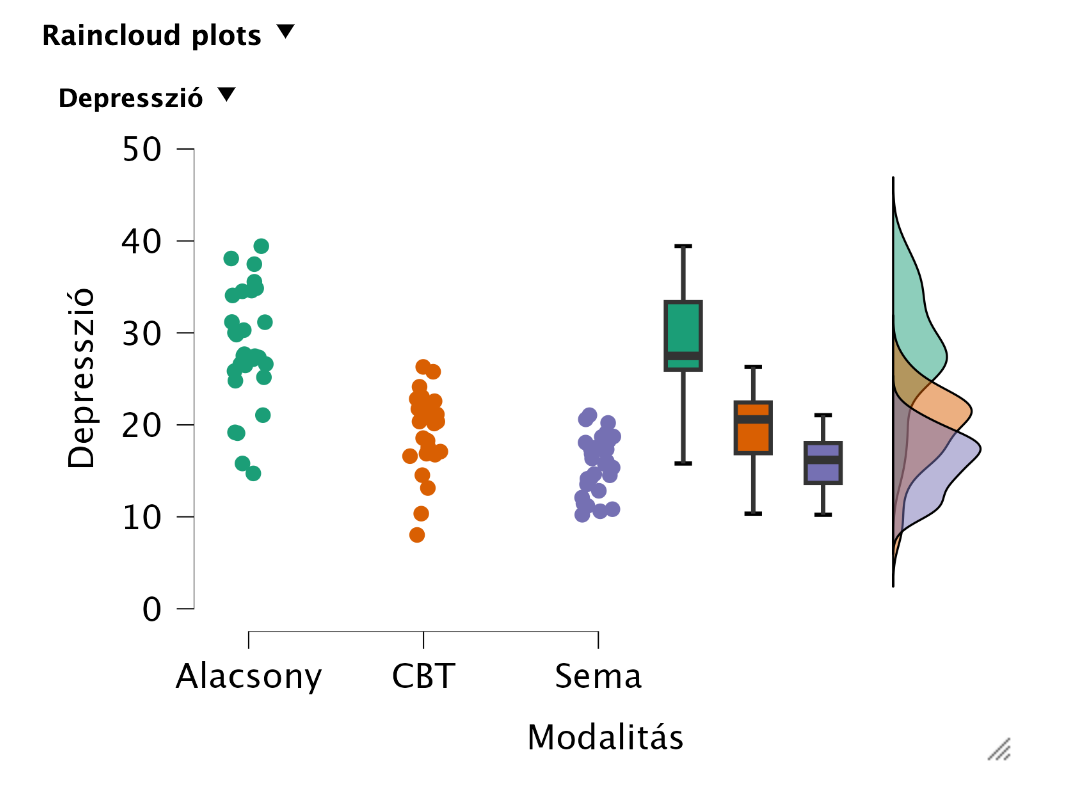
Láthatjuk is vizuálisan, hogy az egyes csoportok szórásai jelentősen eltérnek.
Post-hoc teszt:
Mivel az omnibus F-próba szignifikáns eredményű, és nem volt konkrét erős feltételezésünk, post-hoc tesztet végzünk, hogy exploráljuk a különbségeket.
A beállításokat az alábbiak szerint végezzük el:
- Az Effect size rovatot feltétlenül kipipáljuk, ha nem lenne alapból kipipálva
- Scheffé-féle korrekciót használunk, mert sérülnek az ANOVA feltételei: nem áll fenn a szóráshomogenitás, hiába azonos méretűek a csoportok és nem ismételt méréses vizsgálatot végzünk.
Leolvassuk a post-hoc teszt eredményeit:
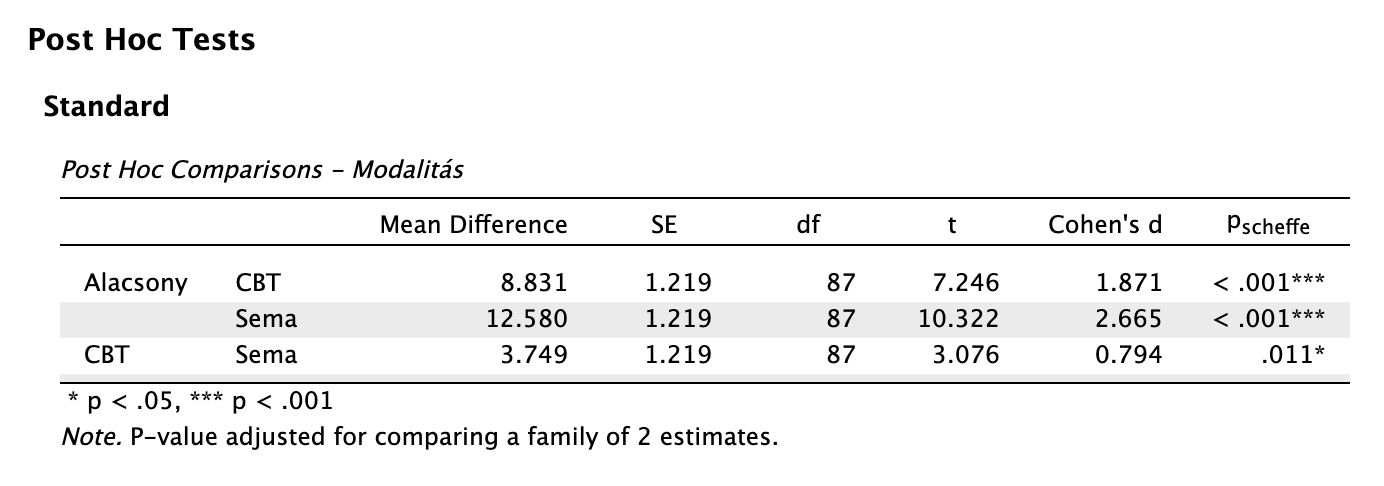
Láthatjuk, hogy mindegyik összehasonlításban szignifikánsak az eredmények (mert pscheffe < 0,05), és nagy Cohen-d hatásnagyságokat láthatunk.
Megoldás 13.2. [Módszerek részben:] A terápiás modalitások összehasonlítására egyszemponos varianciaanalízist (one-way ANOVA) végeztünk. Mivel az éta-négyzet túlbecsüli a hatásnagyságot, az ómega-négyzetet alkalmaztuk az omnibus próba esetén, ami különösen indokolt kis-közepes minták esetén. A post-hoc tesztek során a VA feltételeinek teljesülése esetén Tukey-féle, nem teljesülése esetén Scheffé-féle korrekciót alkalmaztunk.
[Eredmények részben:]2
A terápiás modalitások összehasonlítására végzett egyszemponos VA feltételvizsgálatai alapján a maradványértékek normál eloszlást követtek a QQ plot szemrevételezése alapján, de sérült a csoportok között a szóráshomogenitás feltétele a Levene-próba eredménye szerint (F(2, 87) = 4,823, p = 0,010), ezért Welch-féle (homongenitáskorrigált) varianciaanalízist futtatunk.
A modalitások közötti összkülönbség statisztikailag szignifikáns volt nagy hatásnagysággal: F(2, 54,432) = 48,564, p < 0,001, ω2 = 0,551. Az egyes csoportokra vonatkozó utóvizsgálatok eredménye szerint az alacsony intenzitású csoportnál mért átlagos depressziópontszám (M = 28,34, SD = 6,28) statisztikailag szignifikánsan magasabb mind a CBT (Mdiff = 8,83; t(87) = 7,246, pscheffe < 0,001, d = 1,871), mind a sématerápiás csoport átlagánál (Mdiff = 12,58; t(87) = 10,322, pscheffe < 0,001, d = 2,665). Továbbá statisztikailag szignifikáns különbséget találtunk a sématerápia és kognitív viselkedésterápia között is a sématerápia javára: Mdiff = 3,749, t(117) = 5,488, pscheffe = 0,011, d = 0,794. A különbségek páronként nagy hatásnagyságúak.
[Diszkusszióban értelmezzük, miszerint a sématerápiát gondoljuk hatékonyabbnak a három modalitás közül – ennek a következtetésnek a limitációival együtt.]
13.4 Az egyszempontos ismételt méréses ANOVA (one-way repeated measures ANOVA) feltételei
A vizsgált személyek függetlenek egymástól
Hasonlóan a függetlenmintás t-próbához, feltételezzük, hogy egyik alany válasza a kérdőíves vizsgálaton nem befolyásolja a másik alanyunk válaszát. A személyek/mintaelemek függetlenek. Ezt a kísérleti elrendezésünk kell biztosítsa.
Ugyanazon személyeket mérjük a kísérleti helyzetekben / időpontokban
A függő változó skála típusú
A függő változó (amiben vizsgáljuk a különbségeket) legalább intervallumskála (így kezeljük a Likert kérdőív pontszámait is) mérési szintű. Erről magunk kell meggyőződjünk.
Ha az adataink csupán ordinálisak és nem metrikusak, akkor a nemparaméteres Friedman-próbát alkalmazzuk.
Nincsenek többdimenziós outlierek
Ez nem alapfeltétel, de megbízhatóbb a próbánk eredményének értelmezése, ha ez fennáll. Jelenleg az ANOVA modul a JASP-ban nem tér ki erre a feltételre, mi sem fogjuk vizsgálni.
A függő változó csoportonként normál eloszlású
Ha minden összehasonlítandó csoport elég nagy, akkor a leíró statisztikai modulban a Split segítségével meg tudjuk vizsgálni a függő változó normál eloszlását a Shapiro–Wilk próbával. Ennél fontosabb feltétel azonban a reziduumok normál eloszlása.
Ha a csoportonkénti Shapiro-Wilk próba szignifikáns (tehát p < 0,05 és így nem teljesül a normál eloszlás feltétele), elvégezhetjük a varianciaanalízist, ha:
- a csoportok elemszáma hasonló (< 30% a különbség a legnagyobb és legkisebb csoport elemszáma között)
- csoportonként legalább n > 15 az elemszám
- teljesül a szóráshomogenitás
A legerősebb feltétel: szfericitás (szférikusság), a kondíciók függetlensége
Ez a változók kovarianciamátrixára vonatkozik. Ez a feltétel teljesülni fog, ha az összes lehetséges különbségváltozó szórása azonos, tehát bármelyik két tetszőleges kondíció úgy viszonyul egymáshoz, mint bármelyik másik két tetszőleges kondíció.
Ellenőrzésére a Mauchly-tesztet használjuk. Ha szignifikáns (p < 0,05), akkor a feltétel nem teljesül, mert akkor a kondíciók nem kellő mértékben függetlenek egymástól. Ekkor különféle korrekciókat alkalmazunk a Greenhouse-Geisser epszilon (ti. a korrekciós faktor) értékétől függően:
- Greenhouse-Geisser ε < 0,75: Greenhouse-Geisser-korrekciót alkalmazunk
- Greenhouse-Geisser ε > 0,75: Huynh-Feldt-korrekciót alkalmazunk
Ez a korrekció „lefelé” korrigálja az F-próba szabadságfokát, ezáltal konzervatívabb eredményt kapunk, így csökkentve az elsőfajú hiba valószínűségét.
JASP-ban a Sphericity tests funkció kipipálásval érhető el. A kapott táblábal található értékek:
- Mauchly’s W: a próbastatisztika értéke
- Approx. χ2: közelítő khínégyzet-statisztika, amit jelentünk
- df: a közelítő khínégyzet-statisztika szabadságfoka
- p-value: a próba szignifikanciája
- Greenhouse-Geisser ε: a korrekciós faktor
- Huynh-Feldt ε: alternatív korrekciós faktor
- Lower Bound ε: a korrekciós faktor alsó határa
A feltétel fennállásához a dőlttel szedett statisztikákat jelentjük. Például:
„A Mauchly-féle próba eredménye alapján a szférikusság feltétele sérül (χ2 (df) = …, p = …), ezért a Greenhouse-Geisser-féle korrekciót alkalmazzuk (ε = …).”
13.4.1 Az egyszempontos ismételt méréses ANOVA tábla értelmezése
A JASP outputon láthatjuk, hogy két külön táblázatot kapunk eredményül: egy Within Subjects Effects táblát és egy Between Subjects Effects táblát. Egyszempontos ANOVA esetén ez utóbbinál az F-próba értéke nem lesz kitöltve, hiszen nem határoztunk meg ilyen szempontot. Ezt a többváltozós statisztikában a faktoriális ANOVA esetén tesszük majd. Tehát számunkra a Within Subjects Effects tábla lesz releváns ebben a fejezetben:
Sematikus felépítése a következő:
| Cases | Sum of squares | df | Mean Square | F | p |
|---|---|---|---|---|---|
| Szempont neve (Within subjects) | SSM | dfM | MSM = SSM / dfM | F = MSM / MSR | p |
| Residuals (Within groups) | SSR | dfR | MSR = SSR / dfR |
13.4.2 Példa egyszempontos ismételt méréses varianciaanalízisre (one-way repeated measures ANOVA)
Példa 13.3 (Példa egyszempontos ismételt méréses varianciaanalízisre) Klinikánkon rezisztens depresszióval rendelkező klienseket kezeltünk (n = 40). Minden főnél megvizsgáltuk a depresszió szintjét kérdőíves vizsgálattal négy időpillanatban:
- terápiás intervenció előtt
- terápiás intervenció lezárultakor
- 8 héttel a terápiás intervenció végét követően
- 24 héttel a terápiás intevenció végét követően.
Mindenki részt vett mind a négy mérési időpontban a vizsgálatban. Más szempontot (pl. terápiás módozat stb.) nem vizsgáltunk.
Az adatsor itt letölthető: Rezisztdepr_onewayRM.sav
A megoldás lépéseihez pár kulcsszó:
- varianciaanalízist végzünk, nem pedig páros mintás t-próbát, mert négy időpontot vizsgáltunk
- terápiás módozatot vagy egyéb szempontont nem vizsgáltunk (az majd a többszempontos ANOVA esete lesz)
- magasabb depresszió pontszámot alacsonyabb sikerességnek értékelünk
Állítsuk be a próbát a JASP-ban, de ne olvassuk le még az eredményeket:
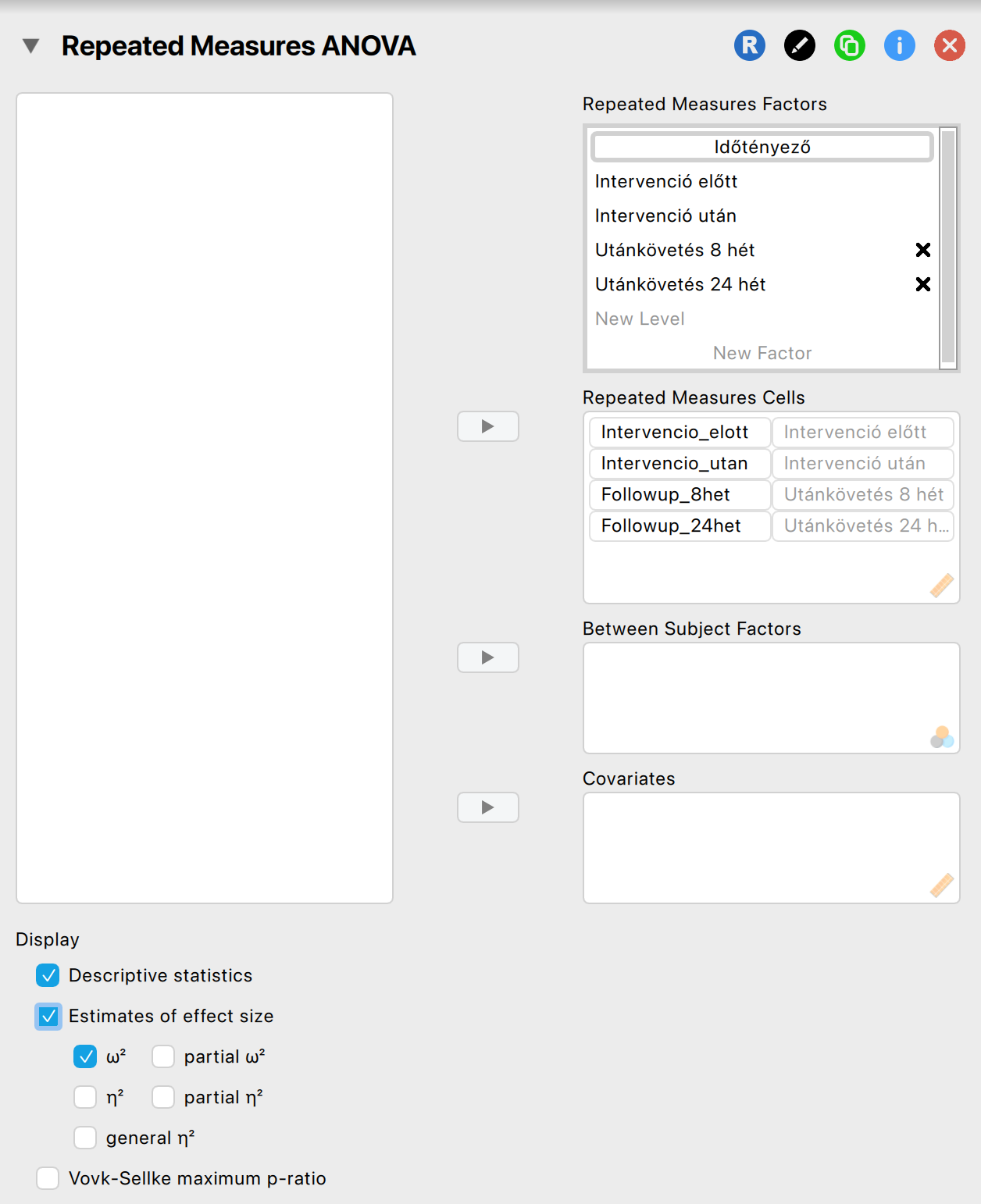
Vizsgáljuk meg a feltételeket:
A vizsgált személyek függetlenek.
Ugyanazokat a személyeket mérjük az egyes időpillanatokban.
A függő változó (ti. depressziópontszám a különböző időpontokban) skála típusú
Többdimenziós outliereket nem vizsgálunk ebben a JASP modulban. (A lineáris regressziós modulban ez rendelkezésre áll pl. Cook-féle távolság.)
A függő változó csoportonként normál eloszlású. Avagy az egyes időpontokban mért depresszió pontszámok (más szempontok és csoportok híján) önmagában normál eloszlást követnek-e. Ezt a leíró statisztikai modulban tudjuk vizsgálni Shapiro-Wilk próbákkal. Mindegyik esetben p > 0,05, tehát a normalitás feltétele teljesül.
Szfericitás: A Mauchly-féle próba eredménye szignifikáns (p < 0,05, mert p = 0,028), ezért a szfericitás feltétele nem teljesül.
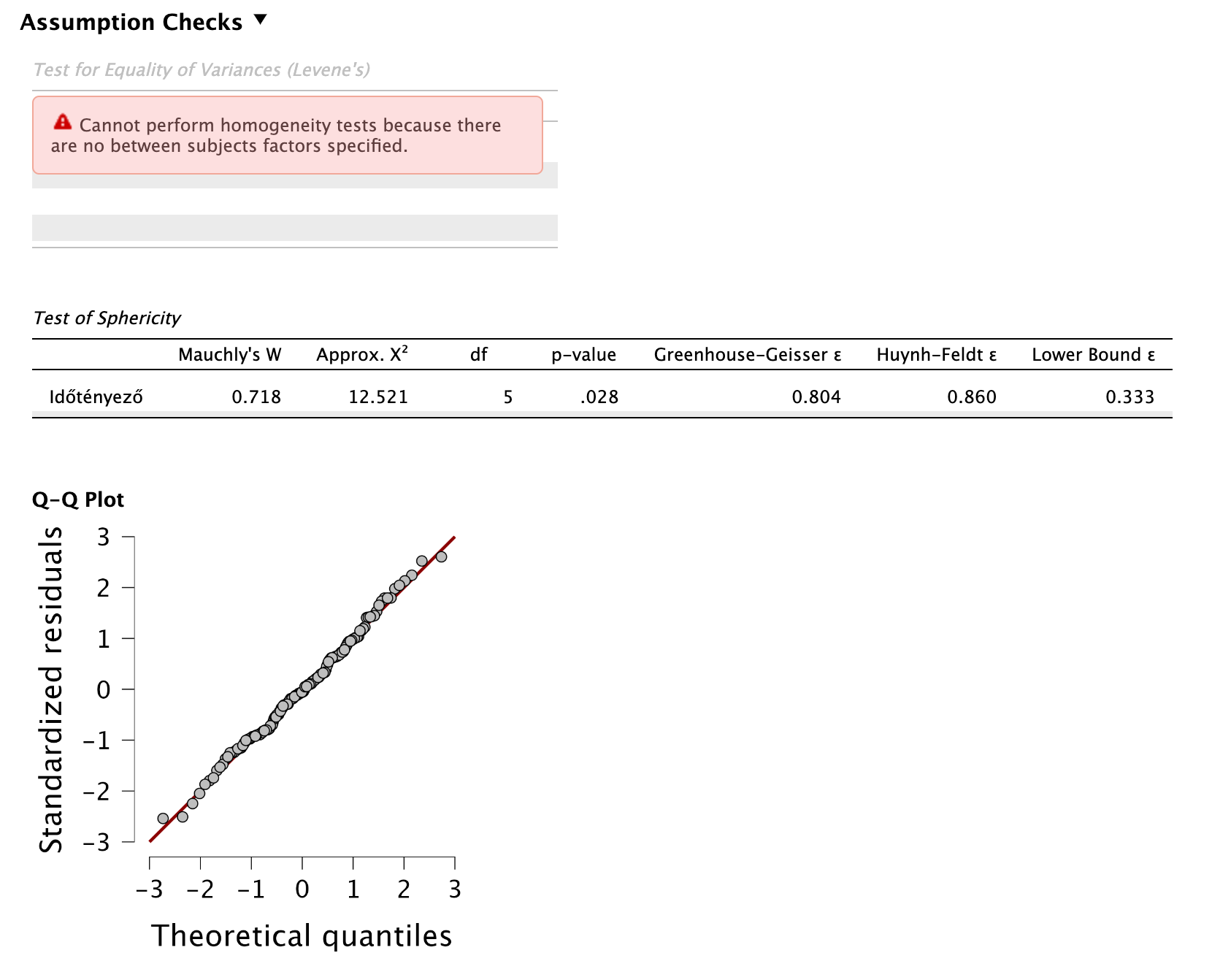
Ez esetben leolvassuk a Greenhouse-Geisser ε értékét. Ez Greenhouse-Geisser ε = 0,804 (> 0,75), ami azt jelenti, hogy Huynh-Feldt-korrekciót alkalmazunk.
ANOVA tábla leolvasása:
Mivel between-subject hatást nem vizsgálunk, csupán a felső ANOVA táblát kell leolvasnunk, de kimondottan a Huynh-Feldt korrekciós értékeket!
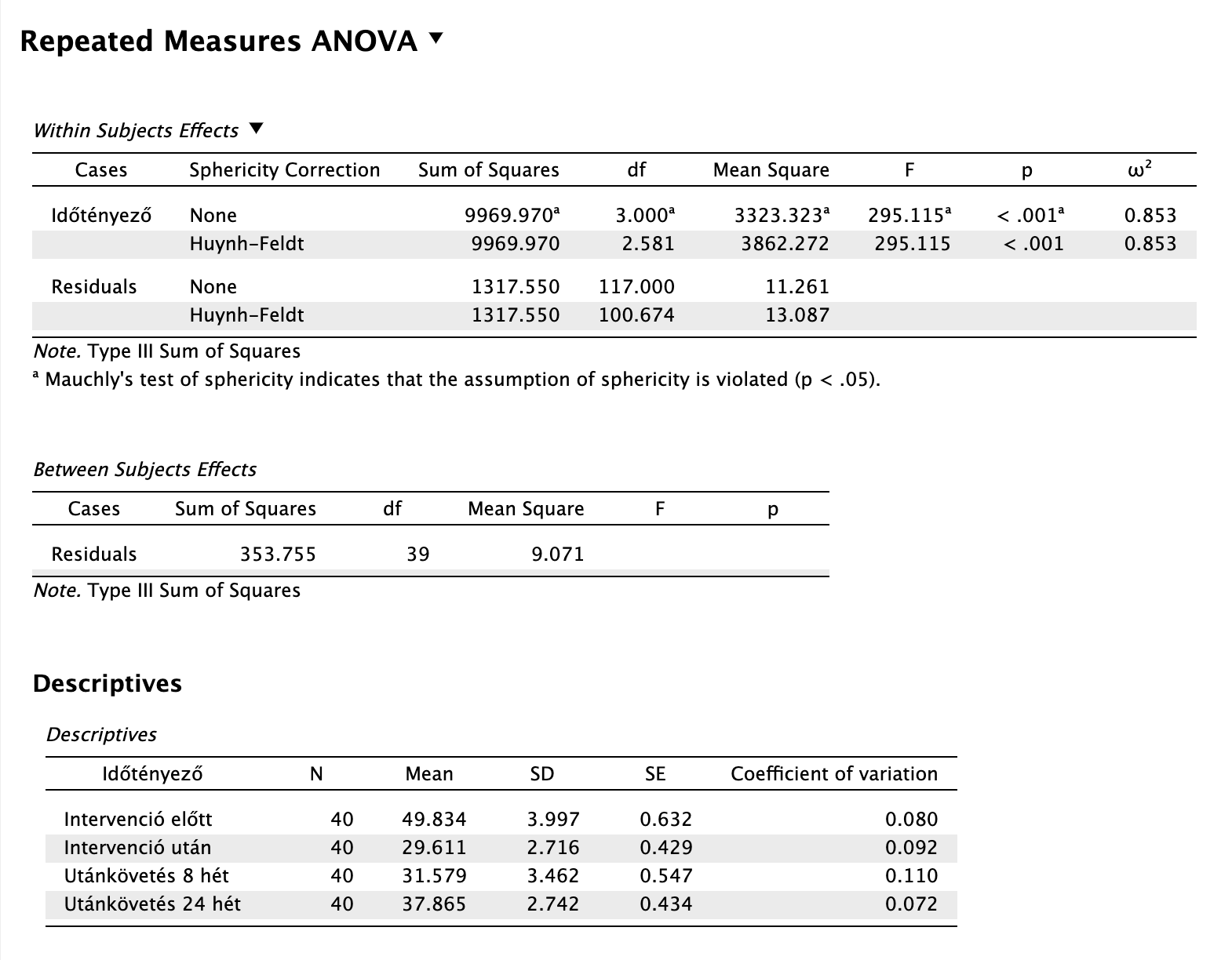
Láthatjuk, hogy az omnibus próba értéke szignifikáns, a hatásnagyság (ω2) nagy.
A leíró statisztikai mutatók között áz átlagok összehasonlításával „szemre” is láthatjuk, hogy viszonylag nagy különbségek vannak az átlagok között. Ezt ábrázolni is tudjuk többféle grafikonnal (Descriptives Plots, Bar Plots, Raincloud Plots). Ezek közül az eloszlásokat is a Raincloud Plots tartalmazza:
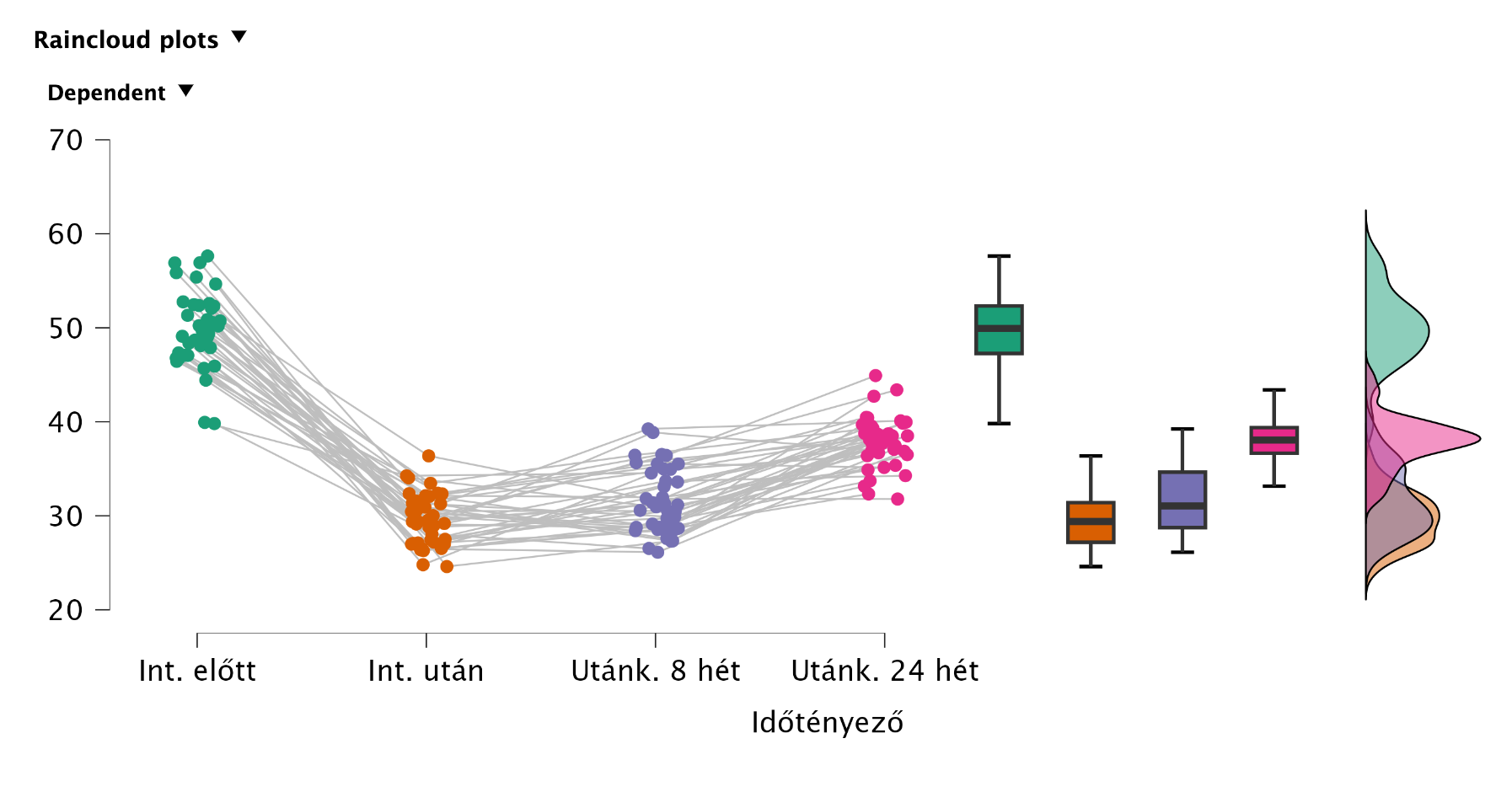
Láthatjuk, hogy a kezdeti magas depressziószint csökken terápiás intervenciót követően, majd fokozatosan emelkedik újra.
Post-hoc teszt:
Mivel az omnibus F-próba szignifikáns eredményű, post-hoc tesztet végzünk, hogy exploráljuk a különbségeket.
A beállításokat az alábbiak szerint végezzük el:
- Effect size funkciót kijelöljük a hatásnagyság kiszámítására
- Holm-féle p-korrekciót alkalmazunk.
Leolvassuk a post-hoc teszt eredményeit:
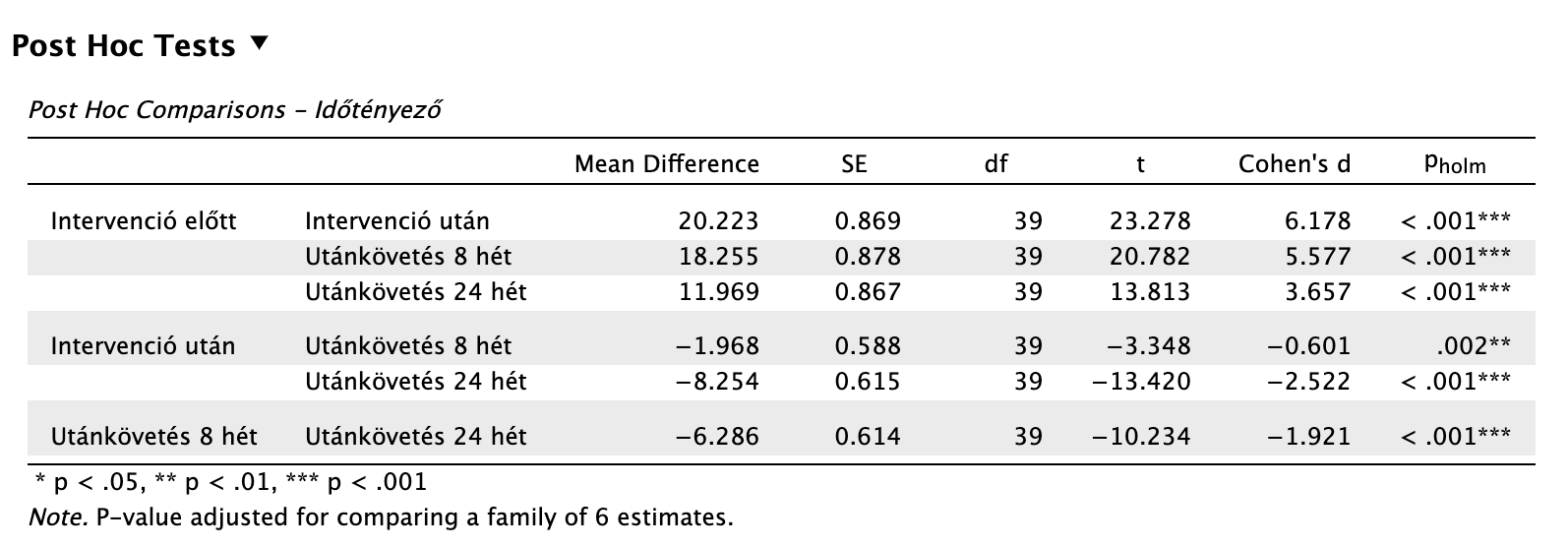
Láthatjuk, hogy minden párosításban szignifikáns különbséget találunk leginkább nagy vagy kiemelkedően nagy hatásnagysággal.
Megoldás 13.3. A depresszió szintjében történő változás utókövetéses vizsgálatára egyszemponos ismételt méréses varianciaanalízist végeztünk. A feltételvizsgálatok alapján az egyes mérések normál eloszlást követtek (Shapiro-Wilk p > 0,05), a maradványértékek normál eloszlást követtek a QQ plot szemrevételezése alapján, de a Mauchly próba eredménye alapján a szfericitás feltétele sérült (χ2 (5) = 12,521, p = 0,028), ezért a Huynh-Feldt-féle korrekciót alkalmazzuk (ε = 0,804).
Az egyes időpillanatok közötti összkülönbség statisztikailag szignifikáns volt nagy hatásnagysággal: F(2,581, 100,674) = 295,115, p < 0,001, ω2 = 0,853. Az egyes időpontokra vonatkozó utóvizsgálatok eredménye szerint terápiás intervenció előtti depresszió pontszám (M = 49,83, SD = 4,00) nagy hatásnagysággal statisztikailag szignifikánsan magasabb, mint bármelyik másik időpillanatban mért depresszió pontszám. Az eredményeket a … számú táblázat tartalmazza:
| Időtényező | Mdiff | t | |
|---|---|---|---|
| Int. előtt | Int. után | 20,223 | t(39) = 23,278, pholm < 0,001, d = 6,178 |
| Int. előtt | Utánk. 8 hét | 18,255 | t(39) = 20,782, pholm < 0,001, d = 5,577 |
| Int. előtt | Utánk. 24 hét | 11,969 | t(39) = 13,813, pholm < 0,001, d = 3,657 |
| Int. után | Utánk. 8 hét | -1,968 | t(39) = -3,348, pholm = 0,002, d = -0,601 |
| Int. után | Utánk. 24 hét | -8,254 | t(39) = -13,420, pholm < 0,001, d = -2,522 |
| Utánk. 8 hét | Utánk. 24 hét | -6,286 | t(39) = -10,234, pholm < 0,001, d = -1,921 |
Az utánkövetéses időszakban a depresszió pontszámok átlagosan újra emelkedtek, de a 24. heti pontszám nem tért vissza az intervenció előtti szintre, különbségük statisztikailag szignifikáns és nagy hatásnagyságú: Mdiff = 11,97, t(39) = 13,813, pholm < 0,001, d = 3,657.
13.5 Az egyszempontos varianciaanalízis nemparametrikus megfelelői
13.5.1 Kruskal-Wallis próba (H-teszt)
Akkor használunk ANOVA helyett Kruskal-Wallis próbát, ha:
- a vizsgált változónk ordinális (és nem skála típusú),
- vagy a normalitás feltétele súlyosan sérül skála típusú változó esetén (erős ferdeség),
- vagy a skála típusú változónk számos extrém értéket tartalmaz, amely nem winzorizálható.
A Kruskal-Wallis próba feltételei:
- A vizsgált személyek függetlenek egymástól.
- A minták (csoportok) függetlenek egymástól.
- A változó legalább ordinális típusú.
A post-hoc vizsgálatokra minden esetben a Dunn-féle post-hoc tesztet javasoljuk, ami a JASP-ban alapértelmezett (és íráskor egyetlen) módszer. Holm és Bonferroni-féle p-érték korrekciót is feltüntet majd az output. Javasoljuk a Holm-korrigált p-érték leolvasását. A hatásnagyságot az rrb rang-biszeriális korrelációs együttható biztosítja, aminek a nagyságát az r korrelációs együtthatóhoz hasonlóan értelmezzük (nem pedig a Cohen-d-hez hasonlóan).
Az átlagok és szórások helyett inkább illik a mediánokat és az interkvartilis terjedelmeket feltüntetni a nemparametrikus próba esetén.
Példa 13.4 (Példa nemparametrikus egyszempontos varianciaanalízisre) Klinikánkon depresszióval diagnosztizált klienseket három csoportra osztva, háromféle terápiás módozatban kezeltük: i) alacsony intenzitású intervenciókkal, ii) kognitív viselkedésterápiával (CBT), valamint iii) sématerápiával. Az intervenciók hosszában nem volt különbség. Az intervenciók előtti depressziós állapotot nem vettük figyelembe. Kíváncsiak vagyunk, hogy melyik volt a hatékonyabb eljárás. Előfeltételezésünk nincs.
Az adatsor itt letölthető: modalitas_nonnormal.sav
A megoldás lépéseihez pár kulcsszó:
- varianciaanalízist végzünk, nem pedig t-próbát, mert három csoportot/módozatot tesztelünk
- mindenki egy csoportba tartozik csak, tehát függetlenek
- az intervenciók hosszában nem volt különbség, így azt mint extra szempontot nem kell most figyelembe vegyük
- a kezelések előtti állapotot nem mértük, tehát nem ismételt méréses elrendezést használunk
- magasabb depresszió pontszámot alacsonyabb sikerességnek értékelünk
- nincs konkrét feltételezésünk egy kimondott modalitásról, hanem összehasonlítani szeretnénk őket, ezért szignifikáns F-próba esetén post-hoc tesztet végzünk, nem pedig kontrasztvizsgálatot.
Állítsuk be a próbát a JASP-ban, de ne olvassuk le még az eredményeket:

Nézzük meg, hogy teljesülnek-e a feltételek:

A személyek függetlenek
A csoportok függetlenek: mindenki csak egy csoportban/módozatban vett részt
A depresszió pontszám skála típusú
Többdimenziós outliert jelenleg nem vizsgálunk JASP-ban. (A lineáris regressziós modulban ez rendelkezésre áll pl. Cook-féle távolság.) De egydimenziós outlierek nincsenek, ezt boxplottal ellenőrizhetjük.
A csoportonkénti normál eloszlás a gyengébb feltétel, de elvégezhetjük a leíró statisztikai modulban. Láthatjuk, hogy egyik esetben sem teljesül a normalitás feltétele, mindhárom csoportnál a Shapiro-Wilk próba szignifikáns (p < 0,001).
A reziduumok normál eloszlását is megvizsgáljuk, ez az erősebb normalitásfeltétel. Ezt a Q-Q plot of residuals funkcióval vizsgáljuk. Láthatjuk, hogy a pontok nem követik szabályosan az átlót, a normalitás mindkét feltétele sérült.
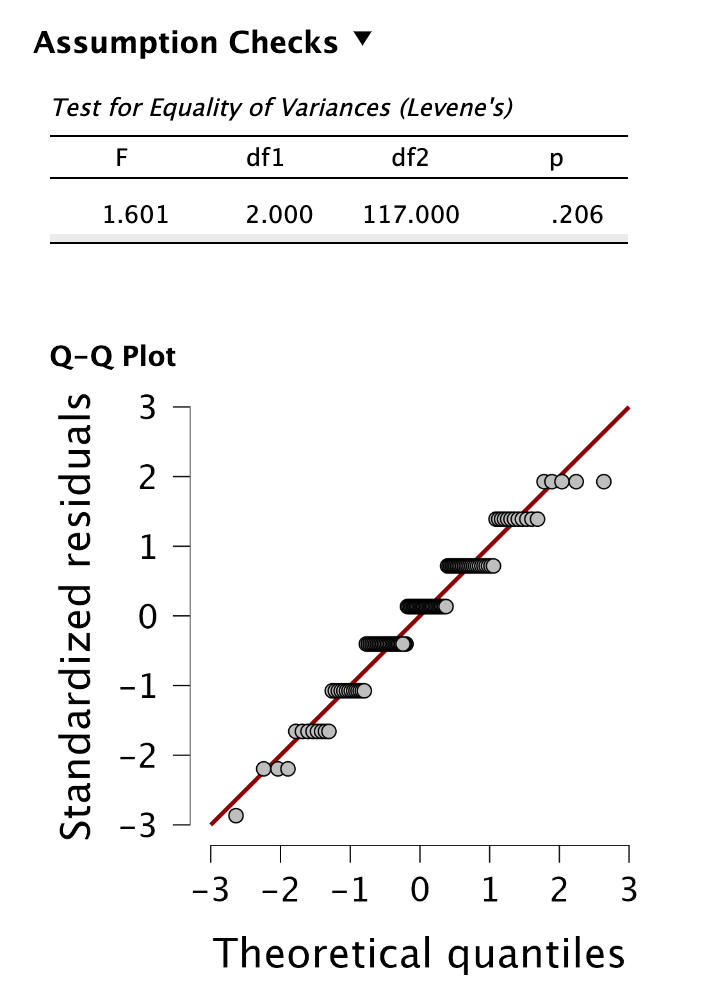
Mindenféleképpen nemparametrikus próbát kell alkalmaznunk!
A szóráshomogenitást a Homogeneity tests funkcióval vizsgálhatnánk, ahol egy Levene-próbát kapunk eredményül, de teljesen szükségtelen, mert az erősen sérült normalitás miatt Kruskal-Wallis nemparametrikus próbát kell alkalmaznunk.
A nemparametrikus próba beállítása:
- Mindenképpen bejelöljük a hatásnagyságot (epszilon-négyzetet választva)
- Szignifikáns próba esetén pedig bejelöljük a Dunn-féle post-hoc tesztet is.
Eredmények leolvasása:
Fontos, hogy semmi esetre se a fő ANOVA táblát olvassuk le, hanem a nemparametrikus próba eredményeit:
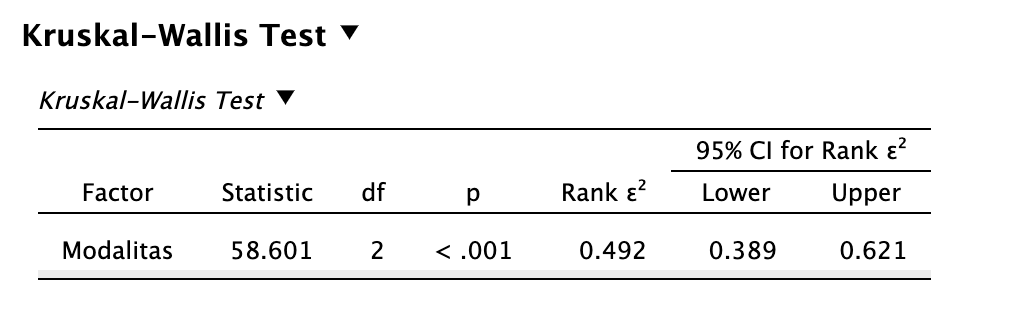
Eredményünk egy χ2-próba (amit H-val is jelölhetünk), hatásnagyásmutatója pedig epszilon-négyzet (ε2).
Vegyük észre első lépésben, hogy a próba p-értéke szignifikáns, tehát van különbség az egyes minták (ti. modalitások) között.
A leíró statisztikai mutatók között áz átlagok összehasonlításával „szemre” is láthatjuk, hogy viszonylag nagy különbségek vannak az átlagok között. Ezt ábrázolni is tudjuk többféle grafikonnal (Descriptives Plots, Bar Plots, Raincloud Plots). Ezek közül az eloszlásokat is a Raincloud Plots tartalmazza:
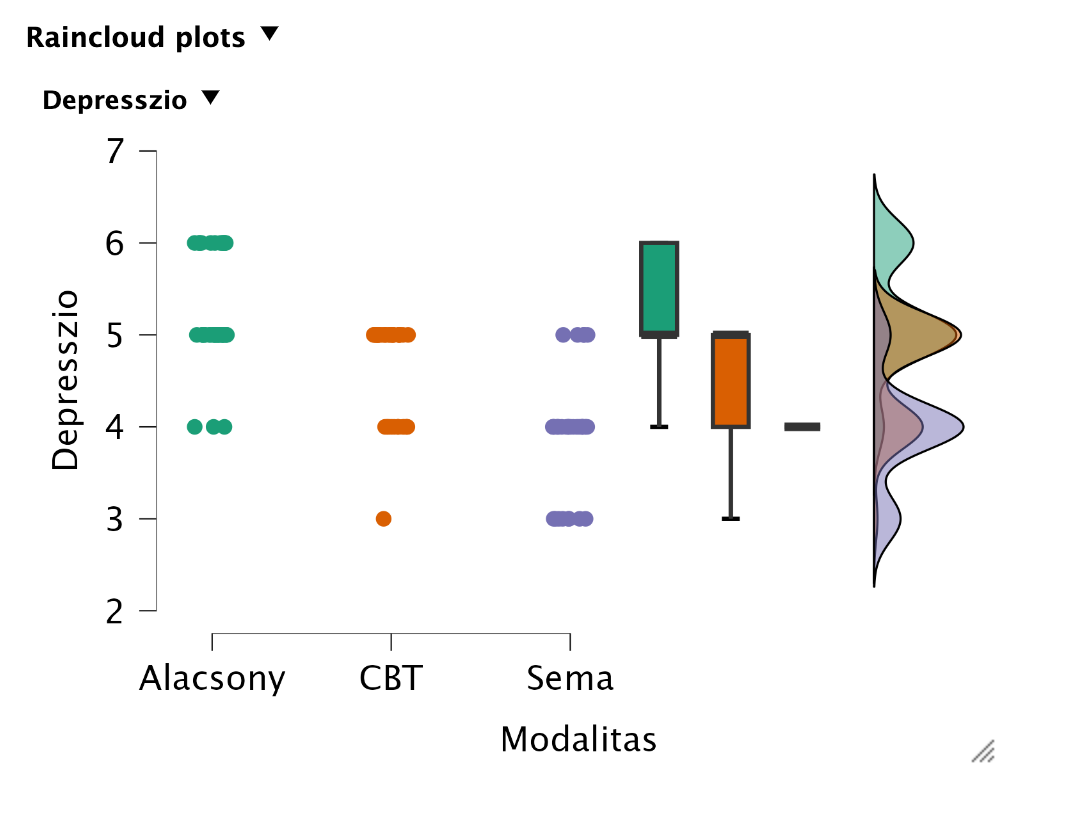
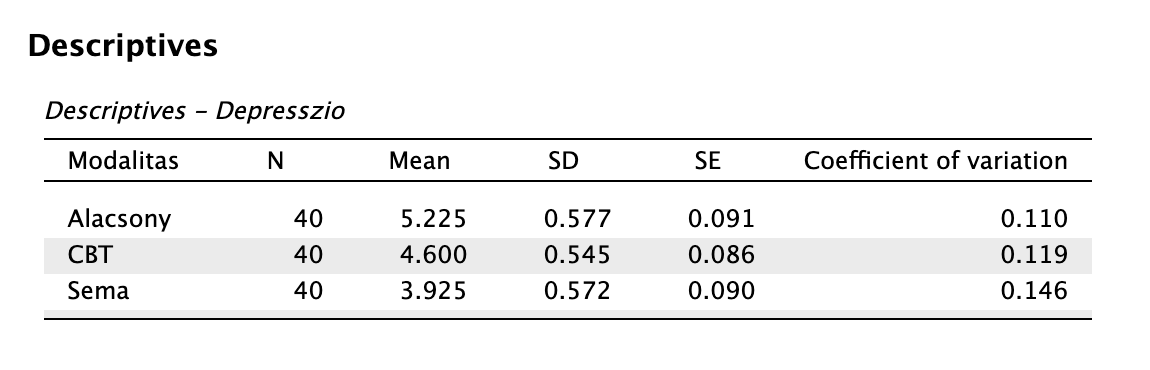
Post-hoc teszt:
Dunn-féle post-hoc tesztet végzünk, hogy exploráljuk a különbségeket. Leolvassuk a post-hoc teszt eredményeit:
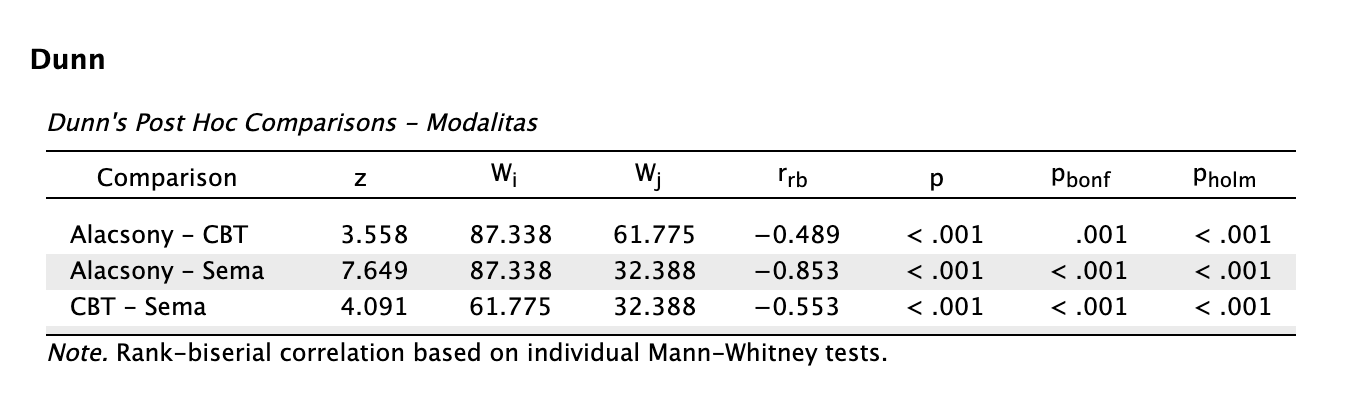
Láthatjuk, hogy mindegyik összehasonlításban szignifikánsak az eredmények (mert pholm < 0,05), és nagy rangbiszeriális korrelációs értékű hatásnagyságokat láthatunk (abszolút értékben értelmezzük).
Megoldás 13.4. A terápiás modalitások összehasonlítására végzett egyszemponos VA feltételvizsgálatai alapján sem a depresszió változónk csoportonként (Shapiro-Wilk próba minden esetben: p < 0,001), sem a maradványértékek nem követték a normál eloszlást (QQ plot eltérő mintázatot mutatott), így Kruskal-Wallis nemparametrikus próbát futtattunk.
A modalitások közötti összkülönbség statisztikailag szignifikáns volt nagy hatásnagysággal: χ2(2) = 58,601, p < 0,001, ε2 = 0,492. Az egyes csoportokra vonatkozó Dunn-féle Holm-korrekciós utóvizsgálatok eredménye szerint az alacsony intenzitású csoportnál mért átlagos depressziópontszám (Med = 5,00, IQR = 1,00) statisztikailag szignifikánsan magasabb mind a CBT (Med = 5,00, IQR = 1,00; z = 3,558, pholm < 0,001, rrb = -0,489), mind a sématerápiás csoport átlagánál (Med = 4,00, IQR = 0,00; z = 7,649, pholm < 0,001, rrb = -0,853). Továbbá statisztikailag szignifikáns különbséget találtunk a sématerápia és kognitív viselkedésterápia között is a sématerápia javára: z = 4,091, pholm < 0,001, rrb = -0,553. A különbségek páronként közepes-nagy hatásnagyságúak.
13.5.2 Friedman-próba
Az ismételt méréses elrendendezések nemparametrikus próbája a Friedman-próba.
Akkor használhatjuk ismételt méréses elrendezés esetén, ha: - a vizsgált változónk ordinális (és nem skála típusú), - vagy a normalitás feltétele súlyosan sérül skála típusú változó esetén (erős ferdeség), - vagy a skála típusú változónk számos extrém értéket tartalmaz, amely nem winzorizálható.
A Friedman-próba feltételei:
- A vizsgált személyek függetlenek egymástól.
- A minták összetartoznak.
- A változó legalább ordinális típusú.
A post-hoc vizsgálatokra minden esetben a Conover-féle post-hoc tesztet használjuk3, ami a JASP-ban alapértelmezett módszer. Holm és Bonferroni-féle p-érték korrekciót is feltüntet majd az output. Itt is javasoljuk a Holm-korrigált p-érték leolvasását. A hatásnagyságot itt is az rrb rang-biszeriális korrelációs együttható biztosítja, aminek a nagyságát az r korrelációs együtthatóhoz hasonlóan értelmezzük (nem pedig a Cohen-d-hez hasonlóan).
Az átlagok és szórások helyett inkább illik a mediánokat és az interkvartilis terjedelmeket feltüntetni a nemparametrikus próba esetén.
Példa 13.5 (Példa nemparametrikus egyszempontos ismételt méréses varianciaanalízisre) Klinikánkon rezisztens depresszióval rendelkező klienseket kezeltünk (n = 40). Minden főnél megvizsgáltuk a depresszió szintjét kérdőíves vizsgálattal négy időpillanatban:
- terápiás intervenció előtt
- terápiás intervenció lezárultakor
- 8 héttel a terápiás intervenció végét követően
- 24 héttel a terápiás intevenció végét követően.
Mindenki részt vett mind a négy mérési időpontban a vizsgálatban. Más szempontot (pl. terápiás módozat stb.) nem vizsgáltunk.
A vizsgálatban azonban csak a terápia lezárulásakori és az utókövetési adatokat használjuk (összesen 3 mérést).
Az adatsor itt letölthető: Rezisztdepr_onewayRM_nonnormal.sav
A megoldás lépéseihez pár kulcsszó:
- varianciaanalízist végzünk, nem pedig páros mintás t-próbát, mert több, mint két időpontot vizsgáltunk
- terápiás módozatot vagy egyéb szempontont nem vizsgáltunk (az majd a többszempontos ANOVA esete lesz)
- magasabb depresszió pontszámot alacsonyabb sikerességnek értékelünk
Állítsuk be a próbát a JASP-ban, de ne olvassuk le még az eredményeket:
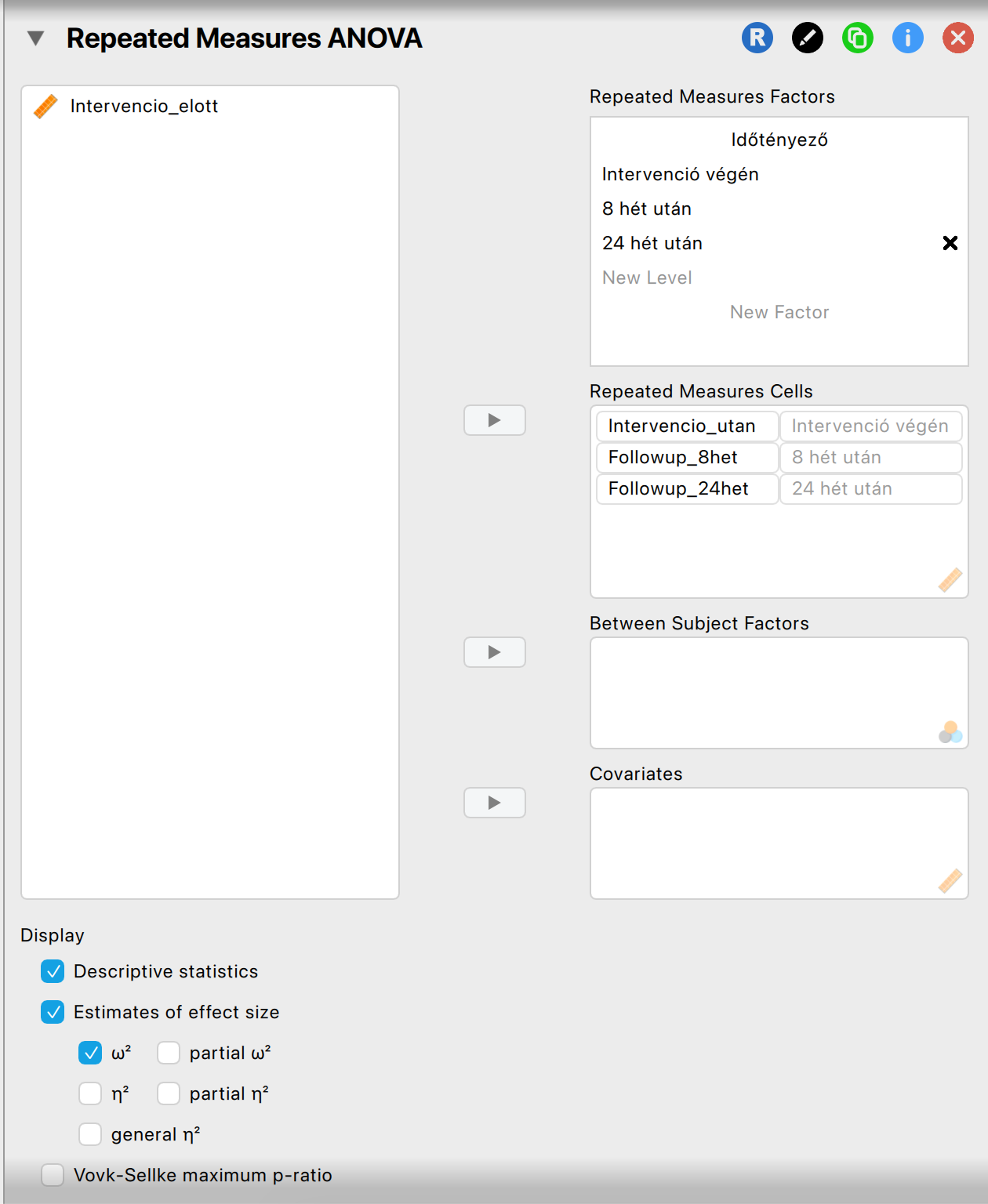
Vizsgáljuk meg a feltételeket:
A vizsgált személyek függetlenek.
Ugyanazokat a személyeket mérjük az egyes időpillanatokban.
A függő változó (ti. depressziópontszám a különböző időpontokban) elvileg skála típusú.
Többdimenziós outliereket nem vizsgálunk ebben a JASP modulban. (A lineáris regressziós modulban ez rendelkezésre áll pl. Cook-féle távolság.)
A függő változó mérésenként nem normál eloszlású. Ezt a leíró statisztikai modulban tudjuk vizsgálni Shapiro-Wilk próbákkal. Mindegyik esetben p < 0,05, tehát a normalitás feltétele sérül! A maradványértékek QQ plotja szintén specifikus mintázatot mutat, ami eltér az elvárt normál eloszlástól.
Ez már önmagában kötelez a Friedman-próba használatára.
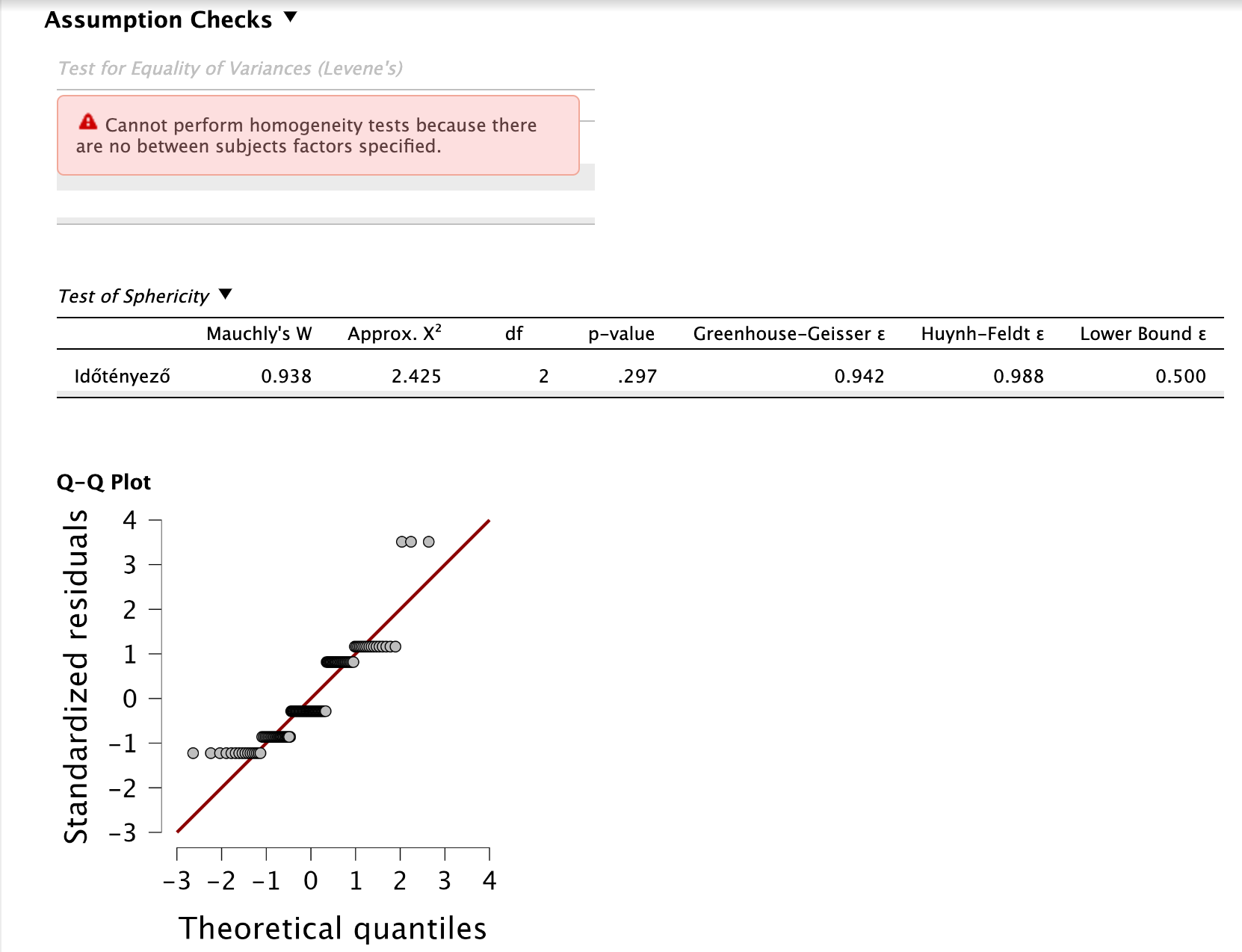
Szfericitás: A Mauchly-féle próba eredménye ugyan nem szignifikáns (p > 0,05), de ez nem is lényeges, mert ez nem feltétele a Friedman-próbának.
A nemparametrikus próba beállítása:
- Szignifikáns próba esetén bejelöljük a Conover-féle post-hoc tesztet.
Eredmények leolvasása:
Fontos, hogy semmi esetre se a fő ANOVA táblát olvassuk le, hanem a nemparametrikus próba eredményeit:
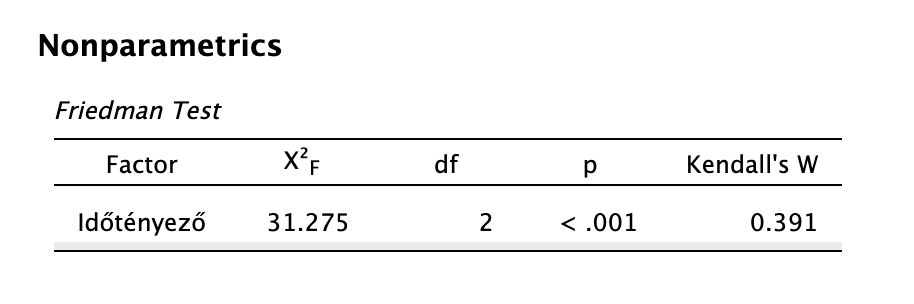
Eredményünk egy χ2-próba. Vegyük észre, hogy a próba p-értéke szignifikáns, tehát van különbség az egyes minták (ti. időpillanatokban mért depressziószint) között.
A leíró statisztikai mutatók között áz átlagok összehasonlításával „szemre” is láthatjuk, hogy nem használhattunk parametrikus próbát:
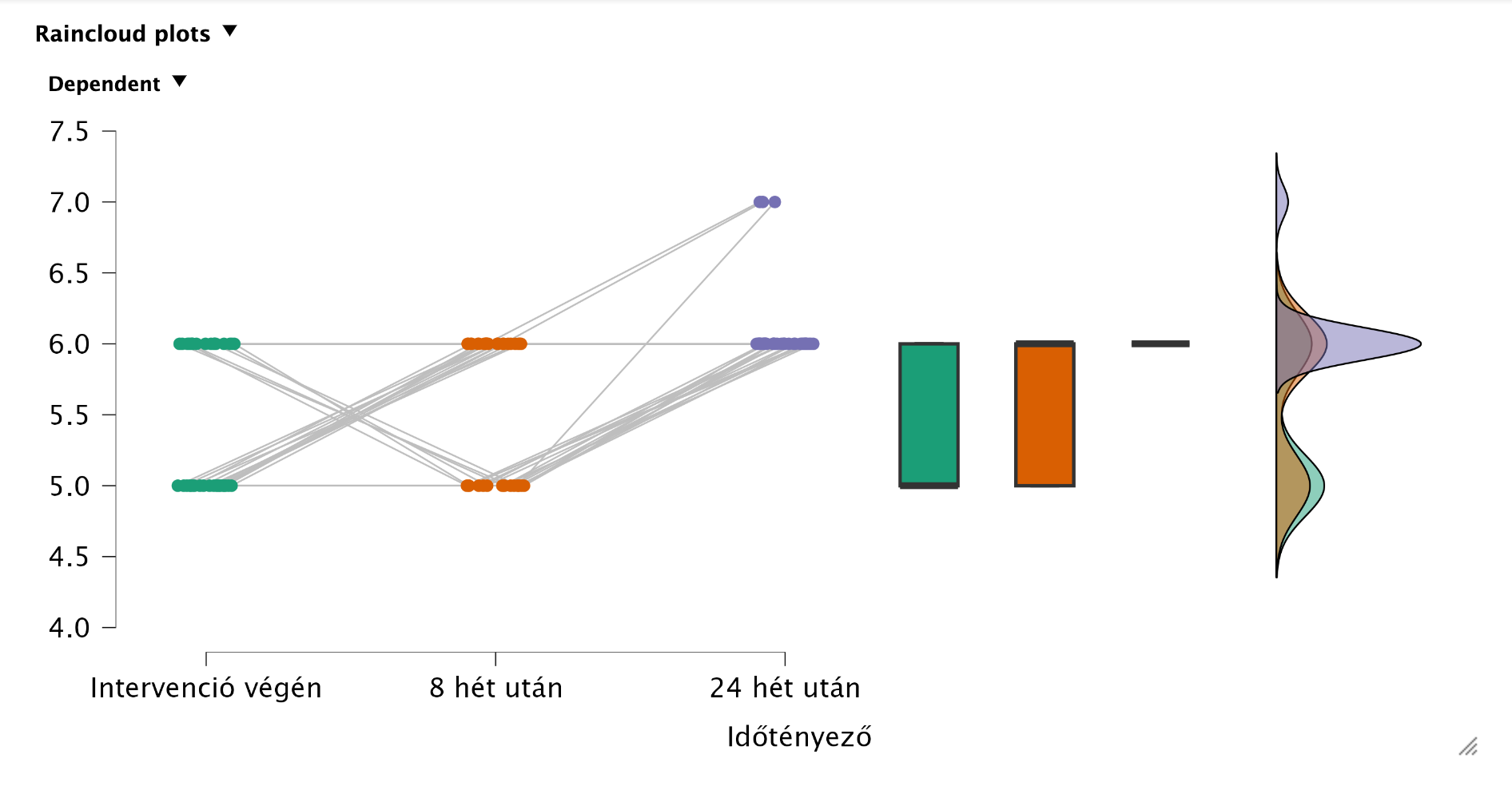
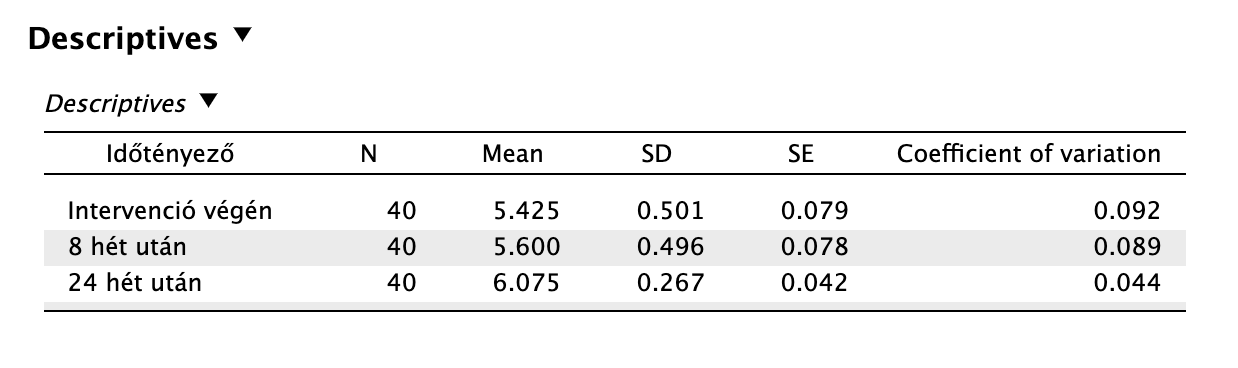
Post-hoc teszt:
Conover-féle post-hoc tesztet végzünk, hogy exploráljuk a különbségeket. Leolvassuk a post-hoc teszt eredményeit:
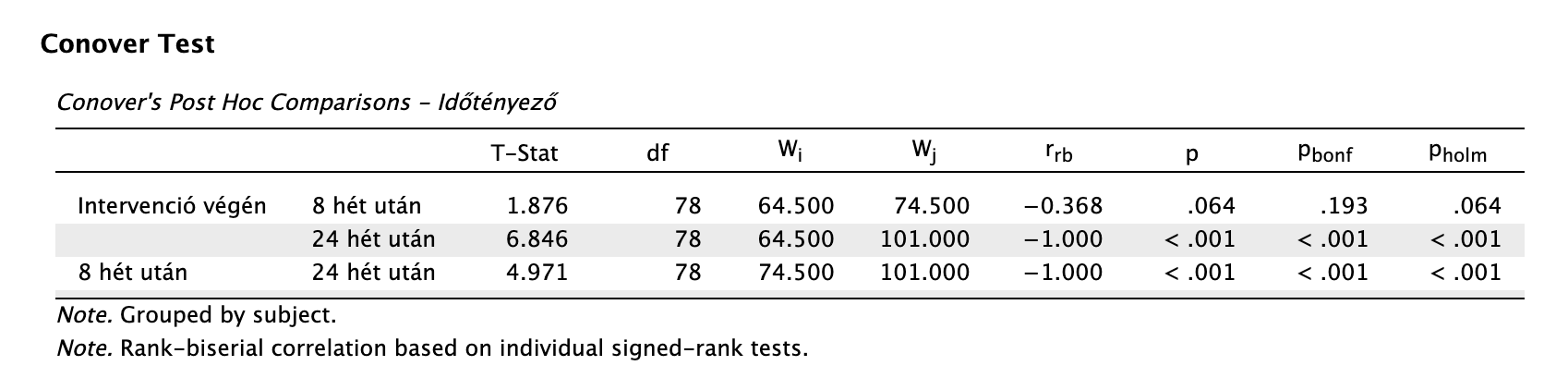
Az intervenció végén mért érték és 8 hét után mért érték között nincs szignifikáns különbség (pholm = 0,064 > 0,05), a többi párosítás esetén van.
Megoldás 13.5. A depresszió szintjében történő változás utókövetéses vizsgálatára egyszemponos ismételt méréses varianciaanalízist végeztünk. A feltételvizsgálatok alapján az egyes mérések nem követtek normál eloszlást (Shapiro-Wilk p < 0,001), és a maradványértékek a QQ plot szemrevételezése alapján olyan mintát követtek, ami összeegyeztethetetlen a normalitással, így Friedman-próbát végeztünk Conover-féle post-hoc vizsgálattal.
Az egyes időpillanatok közötti összkülönbség statisztikailag szignifikáns volt: χ2(2) = 31,275, p < 0,001. Az egyes időpontokra vonatkozó utóvizsgálatok eredménye szerint terápiás intervenció végi depresszió pontszám (Med = 5,00, IQR = 1,00) statisztikailag szignifikánsan nem különbözik a 8 hét utáni értéktől (Med = 6,00, IQR = 1,00; t(78) = 1,876, p = 0,064, rrb = -0,368), azonban szignifikánsan különbözik a 24. heti adatponttól (Med = 6,00, IQR = 0,00; t(78) = 6,846, p < 0,001, rrb = -1,000). Emellett a 8. és 24. hét közötti depressziópontszám is statisztikailag szignifikánsan eltér egymástól: t(78) = 4,971, p < 0,001, rrb = -1,000.
Az eredmény többféleképpen megfogalmazható, felírható. Például a nyersátlagok helyett az átlagok közötti különbség (Mean Difference) is feltüntethető. Egyes publikációkban az átlagok egyáltalán nem szerepelnek itt, hanem külön szekcióban a minta leírásakor, és nem írják ki itt újra. Több, mint három szintű szempont esetén érdemes lehet táblázatosan közölni az eredményeket.↩︎
Az eredmény többféleképpen megfogalmazható, felírható. Itt a nyersátlagok helyett az átlagok közötti különbséget (Mean Difference) tüntettük fel.↩︎
A stathelpen lévő és egyéb SPSS alapú tananyagok ajánlásával ellentétben, semmiképpen sem végzünk páronkénti Wilcoxon próbát szignifikanciakorrekicóval. A Conover-féle post-hoc teszt az új szakmai sztenderd.↩︎