14 Többszempontos varianciaanalízis (factorial ANOVA)

A többszempontos varianciaanalízist faktoriális ANOVA-nak is nevezhetjük. A modellünkben egy folytonos függő változó van, ahogy az egyszempontos (one-way) ANOVA esetén is, és egynél több független diszkrét változónk (faktorunk).

Amikor egynél több szempontot szeretnénk vizsgálni, feloszthatjuk a megmagyarázott varianciát az alábbiak szerint:

graph TD
    SST["SST: Teljes változatosság"]
    SSM["SSM: Megmagyarázott változatosság"]
    SSR["SSR: Reziduálisok"]
    
    SSA["A főhatás"]
    SSB["B főhatás"]
    SSAB["A x B interakció"]
    
    %% Level 1
    SST --> SSM
    SST --> SSR
    
    %% Level 2
    SSM --> SSA
    SSM --> SSB
    SSM --> SSAB

    style SST fill: #97d6f9, stroke: #97d6f9
    style SSM fill: #86BBA8, stroke: #86BBA8
    style SSR fill: #DEE5ED, stroke: #DEE5ED
    style SSA fill: #70B4BE, stroke: #70B4BE
    style SSB fill: #70B4BE , stroke: #70B4BE
    style SSAB fill: #F5BD5F, stroke: #F5BD5F

A főhatás (main effect) egy adott faktor önálló hatását jelenti függetlenül a többi faktortól.

Az interkció (interaction) esetén a főhatások hatnak egymásra: az egyik főhatás „ereje” a másik főhatástól függ. Ha ez szignifikáns, a főhatásokat önállóan tilos értelmeznünk! Erre használjuk később az egyszerű főhatás (Simple Main Effects) elemzést.

14.1 Interakciók

Többszempontos vizsgálat esetén az omnibus F próba ANOVA táblája több főhatást tartalmaz és közöttük lévő interakciós hatást is vizsgálja. Ilyenkor nem tudunk egyszerűen post-hoc tesztet (vagy kontrasztvizsgálatot) végezni, ahogy egyszempontos vizsgálatnál tettük. Meg kell vizsgálnunk ugyanis, hogy szignifikáns-e a kölcsönhatás (interakció) a főhatások között.

Interakció (kölcsönhatás) esetén befolyásolják egymást a főhatások:

Ordinális interakció esetén az adott faktorhoz tartozó hatások sorrendje nem változik a másik faktor szintjei szerint. A hatások egymást erősítik. A hatás mértékében van különbség a szempontok szintjei között.

Például: a depresszió szintjére való hatást tekintve összehasonlítunk terápiás intervenciókat (egyik szempont) és figyelembe veszünk, hogy van-e komorbid szorongásos zavar (másik szempont). Ordinális interakció esetén egyik terápiás módozat jobb, mint a másik, de sikerességének mértéke jobban függ a komorbid zavartól, mint a másik változó esetében. Tehát ilyen esetben a terápiás módozatok hatékonyságai önmagukban is különböznek, a főhatás vizsgálható, ha szignifikáns.
Diszordinális interakció estén egy faktorhoz tartozó hatások sorrendje megváltozik. Keresztező (cross-over) interakció esetén egymás szintjén ellentétes hatás mutatnak. A hatások megfordulnak a szempontok szintjei között.

Például: a depresszió szintjére való hatást tekintve összehasonlítunk terápiás intervenciókat (egyik szempont) és figyelembe veszünk, hogy van-e komorbid szorongásos zavar (másik szempont). Diszordinális interakció esetén nincs egyértelműen jobb vagy rosszabb terápiás módozat, mert a hatékonyság attól függően változik, hogy van-e komorbid szorongásos zavar. Így tehát önmagában nem értelmezhetjük se a terápiás módozatok közti különbséget, se a komorbid zavart mint főhatást.

Ezek alapján az alábbi utóvizsgálatok végezhetők:

Interakció	Főhatás	Post-hoc vagy kontrasztvizsgálat végezhető	Simple Main Effects (SME) vizsgálható
Nem szignifikáns	Nem szignifikáns	❌	❌
”	Egy vagy több főhatás szignifikáns	✅	❌
Szignifikáns, ordinális	Nem szignifikáns	❌	✅
”	Egy vagy több főhatás szignifikáns	✅	✅
Szignifikáns, diszordinális	Nem szignifikáns	❌	✅
”	Egy vagy több főhatás szignifikáns	Lehetséges, de kerüljük, mert félrevezető	✅

14.2 Többszempontos varianciaanalízis (factorial ANOVA) feltételei

A vizsgált személyek függetlenek egymástól

Hasonlóan a függetlenmintás t-próbához, feltételezzük, hogy egyik alany válasza a kérdőíves vizsgálaton nem befolyásolja a másik alanyunk válaszát. A személyek/mintaelemek függetlenek. Ezt a kísérleti elrendezésünk kell biztosítsa.
A független változók (szempontok) függetlenek egymástól (korrelálatlanok)

A Type III Sum of Squares alapbeállítás ezt korrigálja, de a kutatási elrendezésünknek gondoskodnia kell róla, hogy a független változók egymástól függetlenek legyenek.
A függő változó skála típusú változó.
A modell hibatagjai (reziduumok, reziduálisok) normál eloszlást követnek

A modell reziduálisainak normál eloszlását kétféleképpen tudjuk ellenőrizni a JASP protokollban.
- Egyrészt a standardizált reziduálisok Q-Q plotját tudjuk ellenőrizni (mintázat nélkül, a vörös átló mentén helyezkedjenek el az ábrázolt pontok)
- Másrészt a standardizált reziduálisokat exportálni tudjuk önálló oszlopként, és ezen tudunk Shapiro-Wilk próbát futtatni.
Nincsenek többdimenziós outlierek

Ez nem alapfeltétel, de megbízhatóbb a próbánk eredményének értelmezése, ha ez fennáll.

Egyszempontos és faktoriális varianciaanalízis esetén az egydimenziós outliereket teszteljük például IQR módszerrel, szükség esetén winsorizálással.

A többdimenziós outlierek esetén a befolyásos és torzító értékek számítanak, amit Cook-féle távolsággal tudunk ellenőrizni (többféle kritériumszint mellett, legmegengedőbb: Cook D < 1). Ezt a vizsgálatot a Linear Regression modul tartalmazza, az ANOVA nem.
Szóráshomogenitás Levene-teszttel ellenőrizve (between subjects elrendezéseknél)

A JASP ANOVA moduljában található Assumption Checks szekcióban a Homogeneity tests funkció tartalmazza: a Levene-próba áll rendelkezésünkre. (Nem áll itt rendelkezésre Brown–Forsythe-próba.) Azt várjuk, hogy a Levene-próba eredménye ne legyen szignifikáns (vagyis p > 0,05 legyen), mert ez esetben feltételezhetjük, hogy fennáll a szóráshomogenitás az összehasonlítandó csoportok között.

Ha sérül a szóráshomogenitás, a vizsgálat még elvégezhető, ha:
- a csoportok elemszáma hasonló (< 30% a különbség a legnagyobb és legkisebb csoport elemszáma között)
- és a legkisebb és legnagyobb varianciák aránya \(\frac{{VAR}_{max}}{{VAR}_{min}}<4\)
- VAGY ha egyik feltétel sem teljesül, de mégis a kisebb csoporthoz tartozik a kisebb variancia, a nagyobbhoz a nagyobb variancia, akkor korlátozottan értelmezhetjük az ereményeket
Többszempontos ANOVA esetén nem tudjuk alkalmazni a homogenitáskorrekciókat, mint egyszempontos ANOVA esetén, ehhez White-féle korrekciót tudunk alkalmazni R-ben.

White-korrekció (White adjustment):

A JASP R moduljában első futtatás előtt telepítenünk kell a car csomagot. Ezt csak akkor kell megtennünk, ha frissen telepített JASP-unk van és még nem telepítettük fel a csomagot.
```
install.packages("car", repos="https://cran.r-project.org")
```
Ezt követően a csomagot betöltjük:
```
library(car)
```
Az ANOVA modellünket leparaméterezzük. A JASP-ban az adatink oszlopneveit használhatjuk, a JASP kékkel fogja jelölni. A szűretlen adatokra data-ként hivatkozhatunk, a szűrt adatokra filteredData-ként:
```
model <- lm(függőváltozó ~ függetlenváltozóA * függetlenváltozóB, data)
Anova(model, white.adjust="hc3", type="III")
```
Az így kapott omnibus F-próbát a szokott módon tudjuk értelmezni.
Szfericitás (csak ismételt mérés / összefüggő minta esetén) Mauchly-teszttel ellenőrizve (within subjects elrendezésre)
Box M teszttel ellenőrizhető a kovarianciamátrixok homogenitása

Ez egy túlságosan érzékeny vizsgálat, az egyszerű többszempontos ANOVA esetén nem fontos feltétel. A MANOVA (többváltozós varianciaanalízis) esetén lesz kiemelten fontos feltétel, a JASP MANOVA modulja tartalmazza csak ennek megfelelően.

14.3 Többszempontos ANOVA tábla

Sematikus felépítése 2 szempont (A és B faktorok) esetén:

Cases	Sum of squares	df	Mean Square	F	p
A szempont	\(SS_A\)	\(df_A = a - 1\)	\(MS_A = \frac{SS_A}{df_A}\)	\(F_A = \frac{MS_A}{MS_R}\)	\(p_A\)
B szempont	\(SS_B\)	\(df_B = b - 1\)	\(MS_B = \frac{SS_B}{df_B}\)	\(F_B = \frac{MS_B}{MS_R}\)	\(p_B\)
A x B interakció	\(SS_{AB}\)	\(df_{AB} = (a-1)(b-1)\)	\(MS_{AB} = \frac{SS_{AB}}{df_{AB}}\)	\(F_{AB} = \frac{MS_{AB}}{MS_R}\)	\(p_{AB}\)
Residuals	\(SS_R\)	\(df_R = n - (a \times b)\)	\(MS_R = \frac{SS_R}{df_R}\)

Az \(a\) és a \(b\) az A szempont és a B szempont szintjeinek számát jelölik. A teljes megmagyarázott variancia a főhatásokból (\(SS_A, SS_B\)) és az interakcióból (\(SS_{AB}\)) tevődik össze.

Az F-próba hatásnagyságát a parciális mutatókkal vizsgáljuk: parciális ómega-négyzettel ω²_p (ajánlott módszer) vagy parciális éta-négyzettel η²_p.

14.4 Simple Main Effects (egyszerű főhatás)

Az egyszerű főhatáselemzés (Simple Main Effects, SME) elemzés célja, hogy az egyik faktort adott szinten rögzítve vizsgáljuk a másik faktor hatását. Akkor alkalmazzuk, amikor a főhatások között szignifikáns interakció lép fel. Ordinális interakció esetén ajánlott az SME elemzése a post-hoc tesztek mellett, nem ordinális interakció esetén viszont az egyetlen válaszható utóvizsgálat.

14.4.1 Holm procedúra (Holm-Bonferroni korrekció)

A Simple Main Effects az teljes modell hibatagjait használja (pooled error term), tehát nem több önálló one-way ANOVA-nak számítanak, ha precízek vagyunk, de az összehasonlítások száma a halmozott hiba (Familywise error) tekintetében mégis számít. Így a nyers p-értékeket Holm procedúrával korrigáljuk és az α = 0,05 szignifikanciaszinthez hasonlítjuk VAGY más megközelítésben az α = 0,05 szignifikanciaszintünket csökkentjük le.

A procedúra első lépése, hogy sorrendbe állítjuk a p-értékeket.

Például 4 összehasonlítást végeztünk, 4 db p értéket kaptunk:

p = 0,005, p = 0,090, p = 0,030, p = 0,001

Növekvő sorrendbe állítva:

p = 0,001
p = 0,005
p = 0,030
p = 0,090

Ilyen sorrendben 4 (összehasonlítások száma), 3, 2, 1 értékkel a) szorozzuk fel a kapott p-értékeket, hogy Holm-korrigált p_holm értéket kapjunk, amit az α = 0,05 értékhez hasonlítunk VAGY b) az α = 0,05 értéket osztjuk el, hogy korrigált kritériumszintet kapjunk. Amint bármelyik eredményünk nem szignifikáns, megállunk az elemzéssel. Ha szignifikánsnak minősülő tételt találunk ezt követően, azt nem vesszük figyelembe.

megközelítés:

p = 0,001 * 4 -> p_holm = 0,004 < α = 0,05, szignifikáns
p = 0,005 * 3 -> p_holm = 0,015 < α = 0,05, szignifikáns
p = 0,030 * 2 -> p_holm = 0,060 > α = 0,05, nem szignifikáns: MEGÁLLUNK
p = 0,090 * 1 -> p_holm = 0,090 > α = 0,05, nem szignifikáns (úgyse vesszük figyelembe)

megközelítés:

p = 0,001 < α = 0,05 / 4 = 0,0125, szignifikáns
p = 0,005 < α = 0,05 / 3 = 0,0167, szignifikáns
p = 0,030 > α = 0,05 / 2 = 0,0250, nem szignifikáns: MEGÁLLUNK
p = 0,090 > α = 0,05 / 1 = 0,0500, nem szignifikáns (úgyse vesszük figyelembe)

14.5 Példák többszempontos varianciaanalízisre

Példa 14.1 (Példa többszempontos varianciaanalízisre nem szignifikáns főhatás esetén) Kutatásunkban érzelmi jóllétet vizsgáltunk nem, életkor, alkoholfogyasztási szokások és pszichiátriai diagnózisok tükrében. Szeretnénk megvizsgálni, hogy van-e életminőségbeli különbség a pszichiátriai diagnózisok és az alkoholfogyasztási szokások szerint.

A pszichiátriai diagnózisokat BNO-10 kódok szerint rögzítettük:

0: U9990 (Sine morbo)
1: F3200 (Enyhe depressziós epizód)
2: F3210 (Közepes deressziós epizód)
3: F3220 (Súlyos depressziós epizód pszichotikus tünetek nélkül)

Az alkoholfogyasztás szintjei:

0: Nem fogyaszt alkoholt
1: < 7 egység italt fogyaszt egy héten
2: ≥ 7 egység italt fogyaszt egy héten

Az adatsor itt letölthető: erzelmijollet.sav

Állítsuk be a vizsgálatot JASP-ban:

Ellenőrizzük a feltételeket (maradványértékek normál eloszlása, szóráshomogenitás):

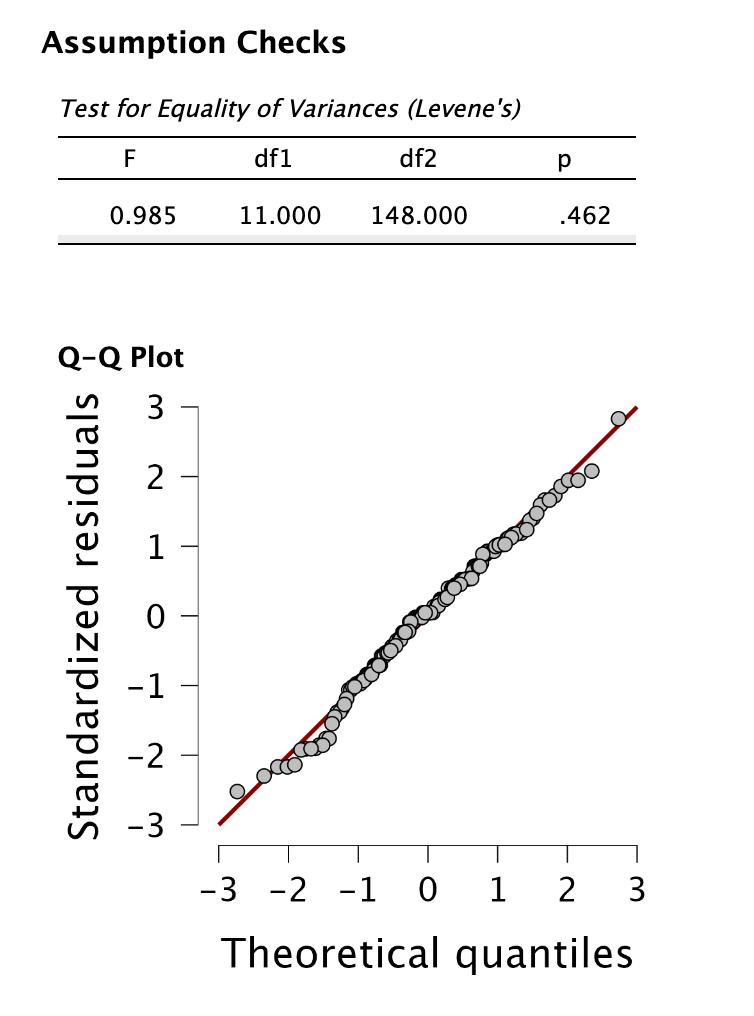
A szóráshomogenitást vizsgáló Levene-próba eredménye nem szignifikáns (p = 0,462 > 0,05), ezért a feltétel nem sérül. A maradványértékek szemrevételezésre normál eloszlást követnek. (Az Export / Append residuals to data (standardized változat) segítségével a maradványértékeket új oszlopként felvehetjük, amelyen Shapiro-Wilk próba végezhető.)

Leolvashatjuk az ANOVA táblát:

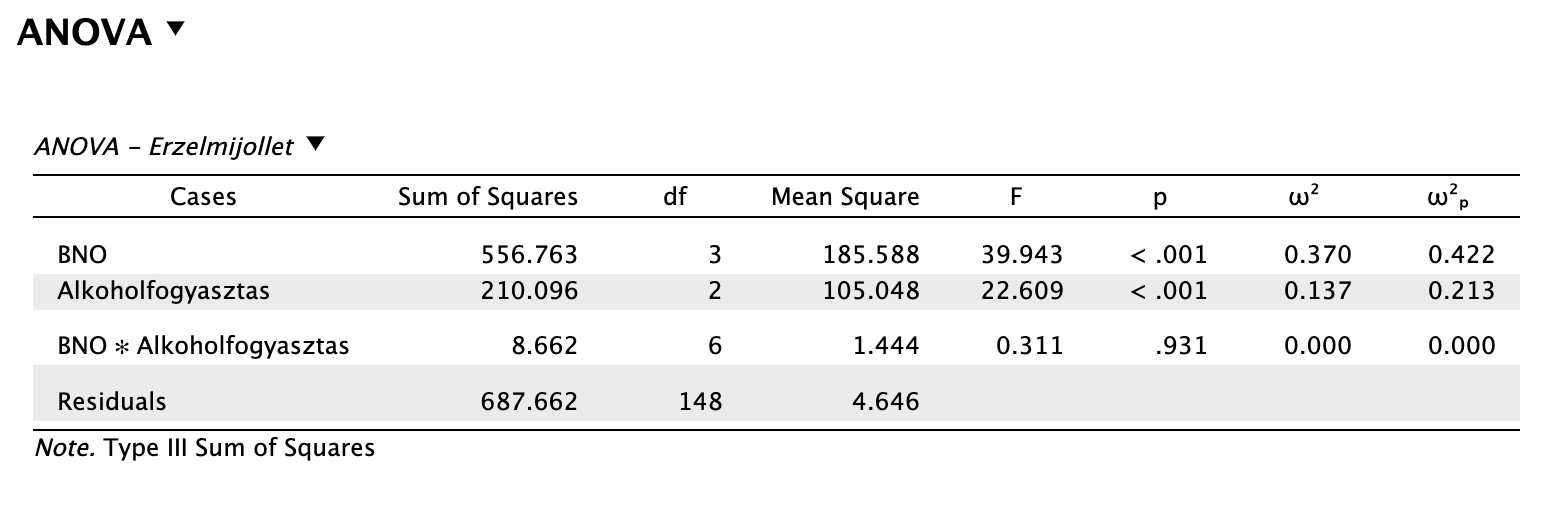
Láthatjuk, hogy a diagnózisok és alkoholfogyasztási szint esetén is szignifikáns főhatásokról beszélhetünk, míg a két szempont interakciója nem szignifikáns.

Szemléltessük az eredményeket a könnyebb megértés érdekében:

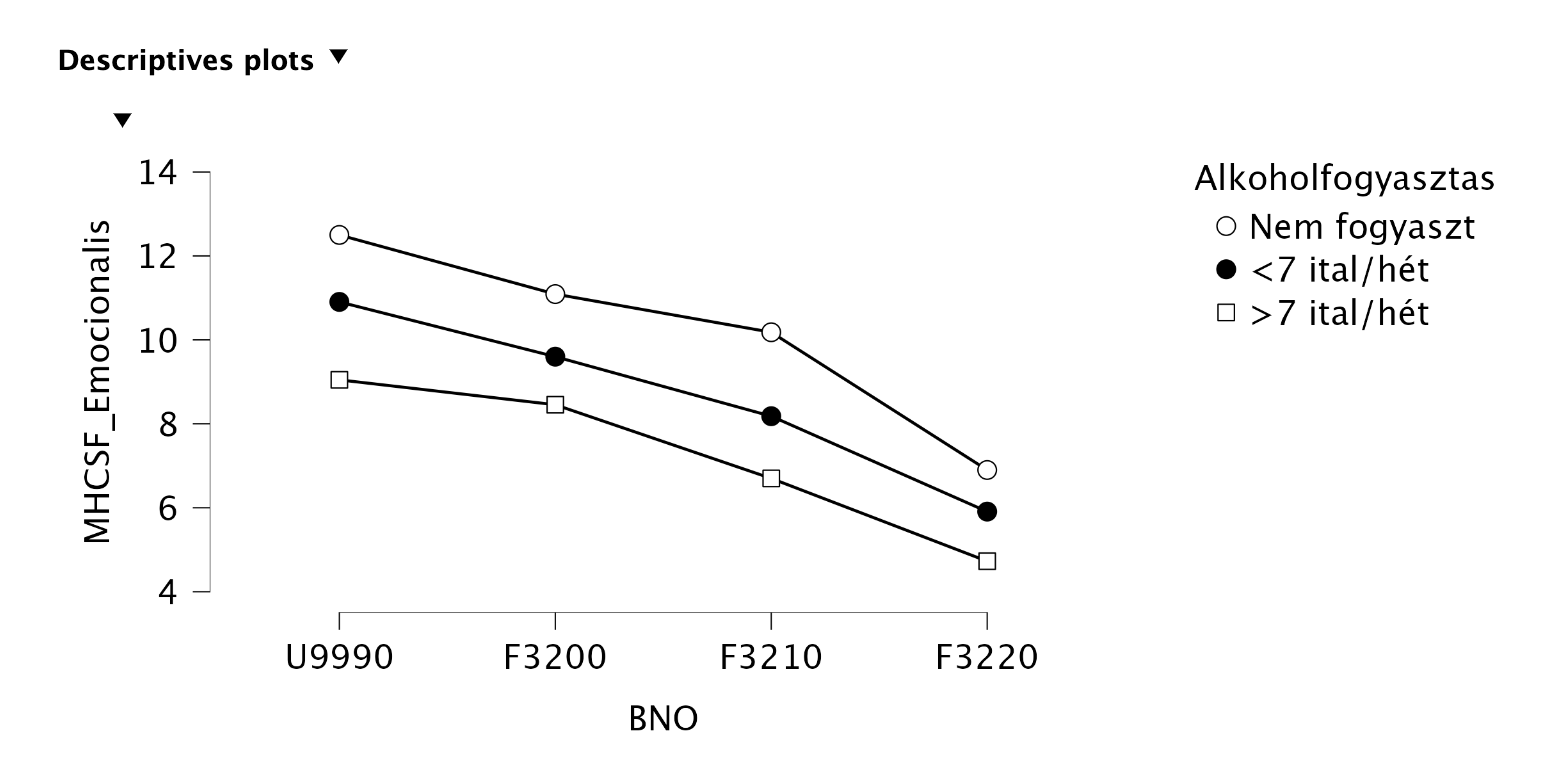
Leolvashatjuk, hogy minél súlyosabb depresszióval diagnosztizáltak valakit, annál alacsonyabb az érzelmi jólléte (diagnózis főhatás). Azt is látjuk, hogy következetesen magasabb jóllét pontszáma van annak, aki minél kevesebb alkoholt fogyaszt (alkoholfogyasztás főhatás). Az ábrán nagyjából azonos ütemű csökkenések és távolságok láthatók, nincs ollószerű „szétnyílás” (ordinális hatás), se sorrendváltás (diszordinális hatás): ez egybecseng a nem szignifikáns interakcióval.

Az ANOVA táblában láthatjuk a parciális ómega-négyzet ω²_p mutató alapján, hogy a diagnózis szempontunk a modell varianciájának 42,2%-át magyarázza (ω²_p = 0,422), míg az alkoholfogyasztási szokások a variancia 21,3%-át magyarázzák.

Post-hoc vizsgálatot végzünk az eredmények bővebb feltárására. Az omnibus F próba ugyanis csak szignifikáns hatást mutatott, de nem mondja meg bővebben, hogy hol találhatók szignifikáns és nem szignifikáns eltérések a szintek között. Tukey-féle korrekciót használunk, mert feltételeink nem sérültek.

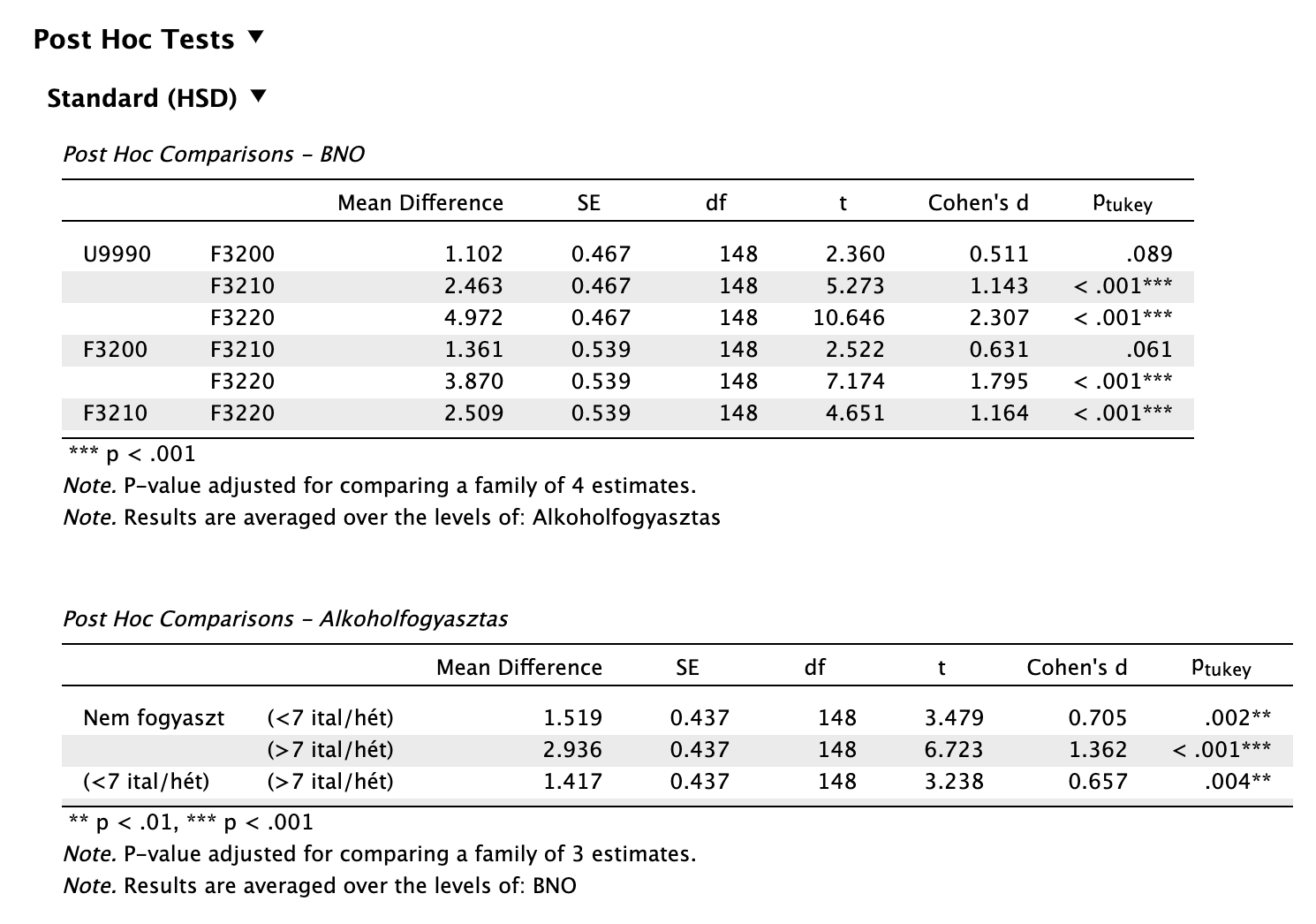
Láthatjuk, hogy az alkoholfogyasztás minden szintpárján szignifikáns különbséget találunk közepes és nagy hatásnagysággal. Legnagyobb különbség - ahogy az feltételezhető volt - a „nem fogyaszt” és „>7 egyés ital/hét” szintek között van.

A diagnózisok szempontjai között találunk szignifikáns és nem szignifikáns különbségeket is. Láthatjuk, hogy a diagnózis nélküli (Sine morbo U9990) és Enyhe depressziós epizód (F3200) között nincs statisztikailag szignifikáns különbség az átlagos alkoholfogyasztási szinten, és ugyanez igaz az Enyhe (F3200) és Közepes (F3210) szintek között is. A többi összehasonlítási párban a különbség szignifikáns és jelentős, 1 fölötti hatásnagysággal.

Megoldás 14.1. Többszempontos varianciaanalízissel ellenőriztük, hogy az érzelmi jóllét milyen mértékben magyarázható a depresszió diagnózis súlyosságával és az alkoholfogyasztási szokásokkal. A maradványértékek normalitásának feltétele teljesül a QQ plot szemrevételezése és Shapiro-Wilk próba alapján (W(160) = 0,990, p = 0,286). A szóráshomogenitás feltétele szintén nem sérül a nem szignifikáns Levene-próba eredménye alapján (F(11, 148) = 0,985, p = 0,462).

Nem található szignifikáns interakció a diagnózis és alkoholfogyasztási szokások között (F(6, 148) = 0,311, p = 0,931, ω²_p = 0,000).

Statisztikailag szignifikáns főhatást találtunk a depresszió súlyossága (BNO szerinti jelölések szintje) szerint (F(3, 148) = 39,943, p < 0,001, ω²_p = 0,422), ami a modellünk varianciájának 42%-át magyarázza. Tukey-korrigált post-hoc vizsgálat eredménye alapján a kontrollcsoport és enyhe depresszió (p = 0,089, d = 0,511), valamint az enyhe és középsúlyos depresszió szintek között (p = 0,061, d = 0,631) nem volt szignifikáns különbség a jóllétet tekintve átlagos alkoholfogyasztás mellett. A többi szint között már statisztikailag szignifikáns, nagy hatásnagyságú különbséget találtunk, amit a … táblázat tartalmaz:

		Átlagkülönbség	SE	df	t	Cohen d	p_tukey
U9990	F3200	1,102	0,467	148	2,360	0,511	0,089
	F3210	2,463	0,467	148	5,273	1,143	< 0,001
	F3220	4,972	0,467	148	10,646	2,307	< 0,001
F3200	F3210	1,361	0,539	148	2,522	0,631	0,061
	F3220	3,870	0,539	148	7,174	1,795	< 0,001
F3210	F3220	2,509	0,539	148	4,651	1,164	< 0,001

Szintén szignifikáns főhatást találtunk az alkoholfogyasztási szintek tekintetében (nem fogyasz, <7 egység, >7 egység hetente): F(2, 148) = 22,609, p < 0,001, ω²_p = 0,213, ez a modellünk varianciájának 21%-át magyarázza. A Tukey-korrigált post-hoc vizsgálat alapján diagnózistól függetlenül minden alkoholfogyasztási szint között szignifikáns különbség van az érzelmi jóllétben (p < 0,05) közepes és nagy hatásnagyságban. Az eredményeket a … táblázat tartalmazza:

		Átlagkülönbség	SE	df	t	Cohen d	p_tukey
Nem fogyaszt	< 7 ital	1,519	0,437	148	3,479	0,705	0,002
	> 7 ital	2,936	0,437	148	6,723	1,362	< 0,001
< 7 ital	> 7 ital	1,417	0,437	148	3,238	0,657	0,004

A csoportkülönbségeket a … ábra szemlélteti:

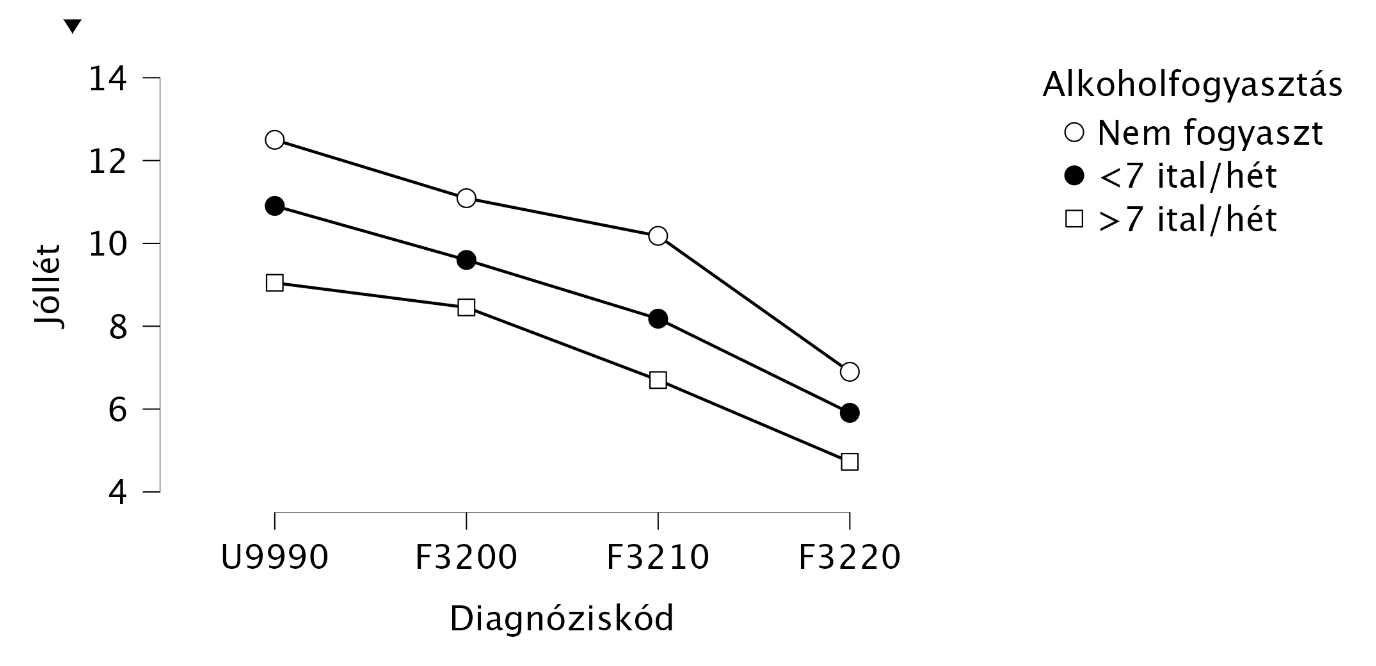
Példa 14.2 (Többszempontos varianciaanalízisre szignifikáns interakció mellett) Kutatásunkban férfiak és nők fizikai egészségét vizsgáltuk haskörfogat mérete és korcsoport szerint. Az általános indikáció szerint férfiak esetén 102 cm és nők esetén 88 cm feletti haskörfogat erős prediktora a szív- és érrendszeri betegségeknek.

Az adatsor itt letölthető: haskorfogat_egeszseg.sav

Állítsuk be a vizsgálatot JASP-ban:

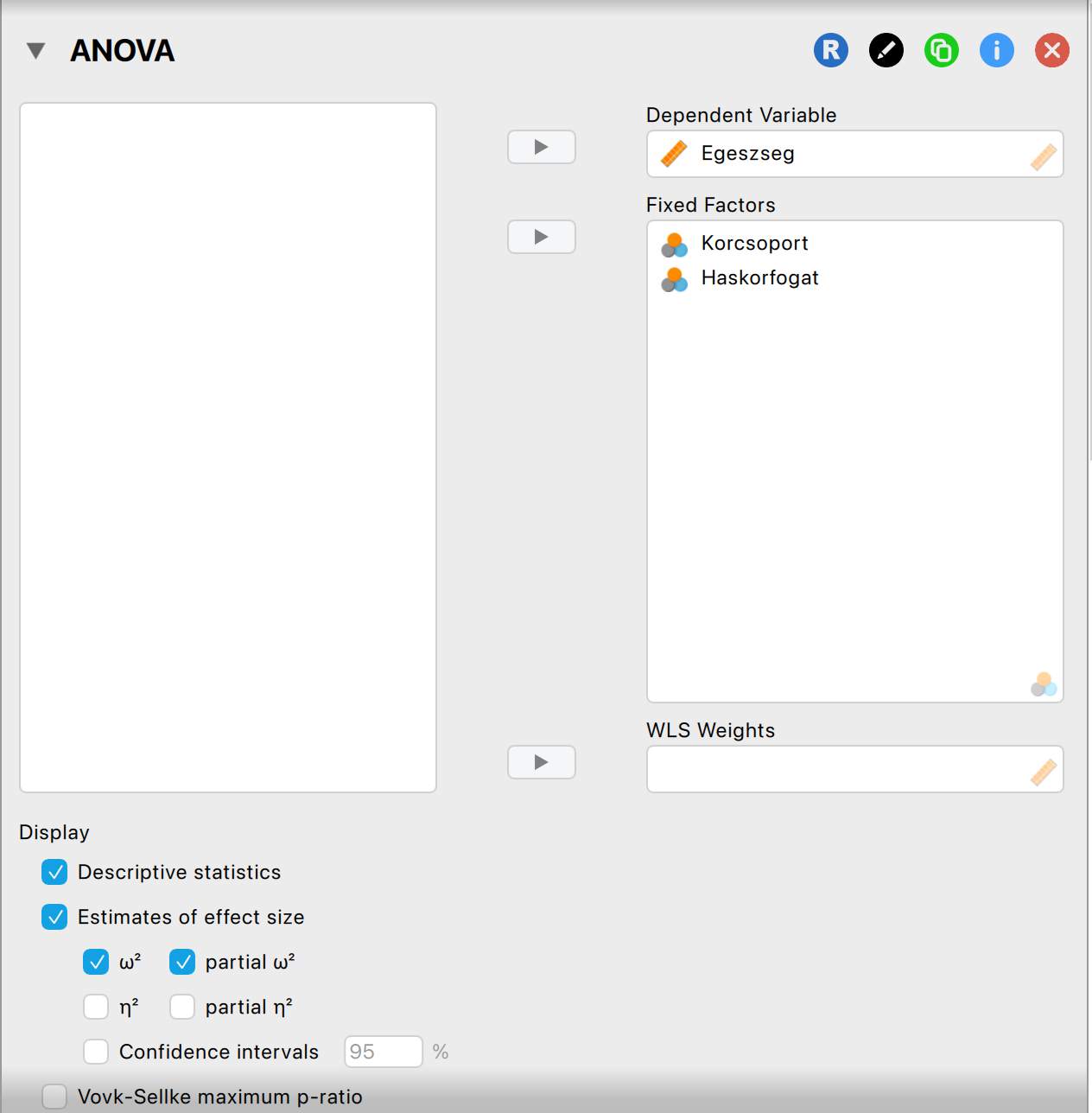
Ellenőrizzük a feltételeket (maradványértékek normál eloszlása, szóráshomogenitás):

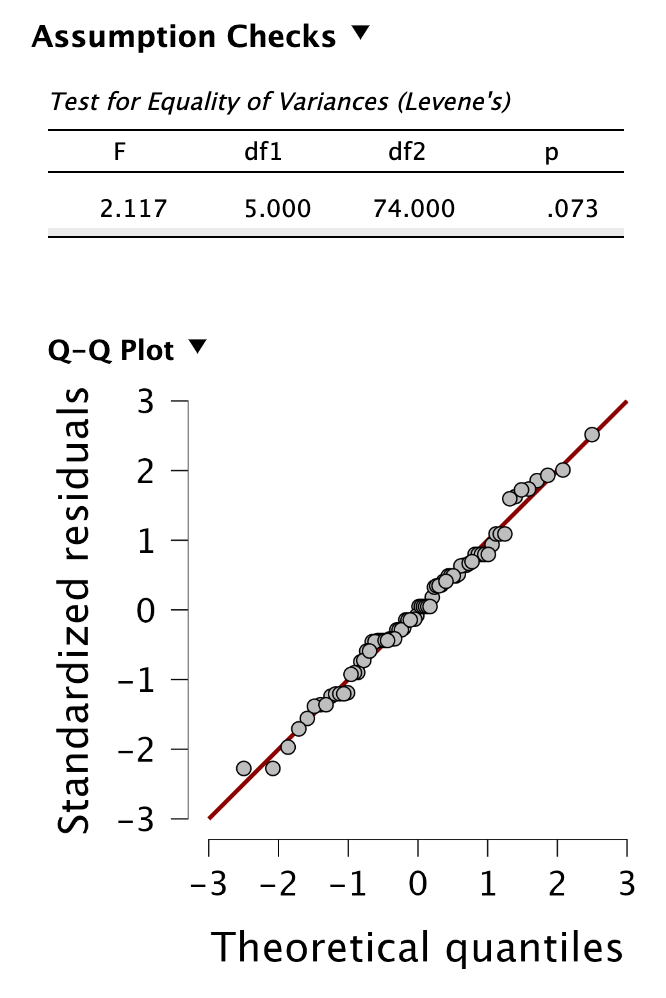
A szóráshomogenitást vizsgáló Levene-próba eredménye nem szignifikáns (p = 0,073 > 0,05), ezért a feltétel nem sérül. A maradványértékek szemrevételezésre normál eloszlást követnek. (Az Export / Append residuals to data (standardized változat) segítségével a maradványértékeket új oszlopként felvehetjük, amelyen Shapiro-Wilk próba végezhető.)

Leolvashatjuk az ANOVA táblát:

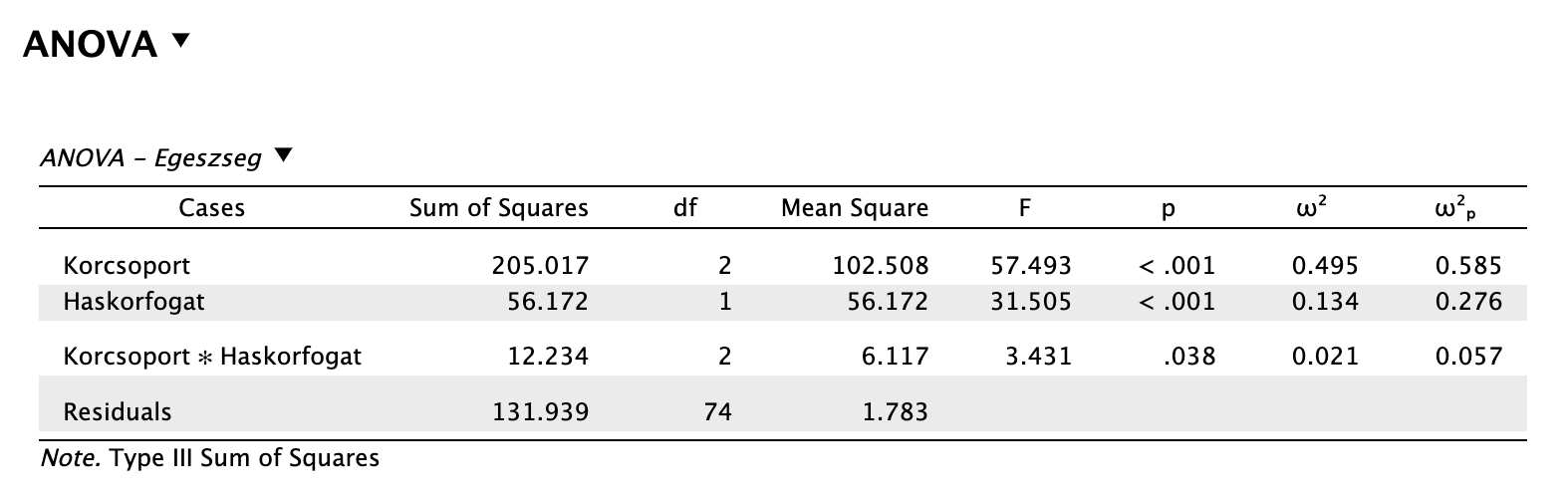
Vegyük észre először is, hogy az interakció szignifikáns! Ez azt jelenti, hogy a faktorok hatása egymástól függően változik. Ilyen esetben főhatásokként önállóan nem értelmezzük őket, illetve szükségünk lesz Simple Main Effects elemzésre.

Szemléltessük az eredményeket a könnyebb megértés érdekében:

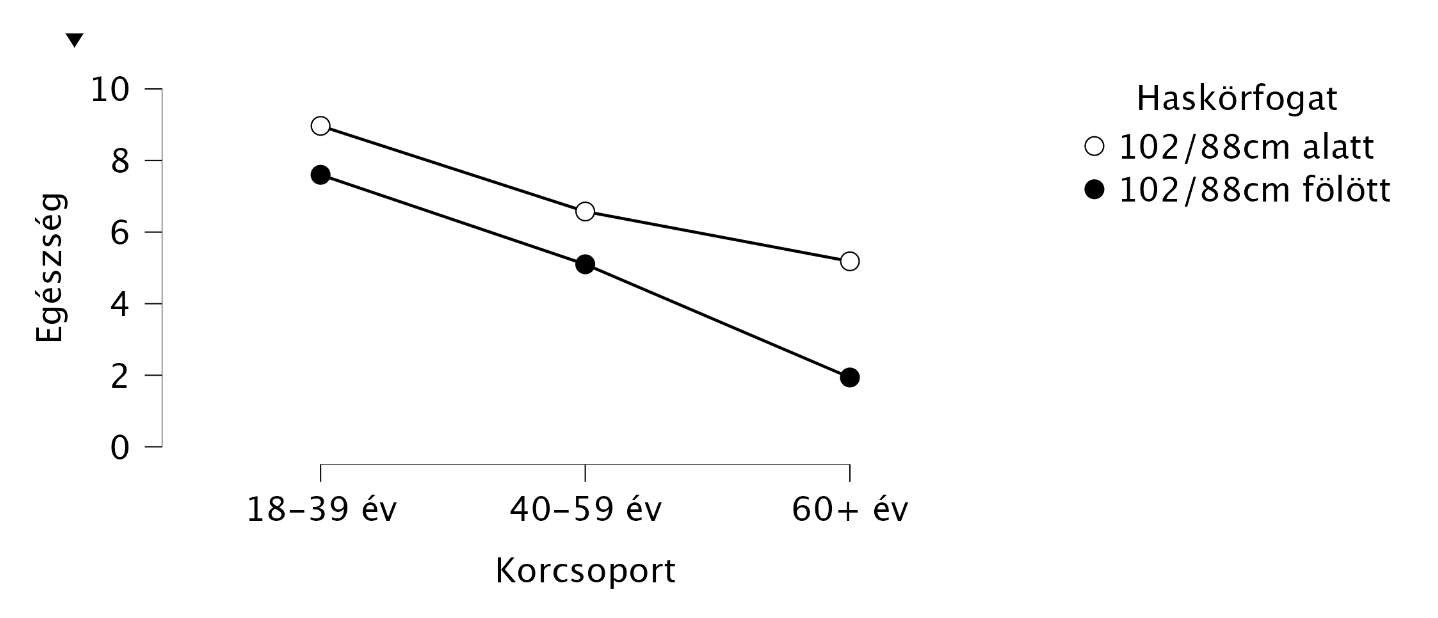
Láthatjuk, hogy ordinális interakcióról van szó, mert „nyíló olló” alakot láthatunk és nincs kereszteződés. Leolvashatjuk az ábráról, hogy a 102/88 cm haskörfogat feletti személyek rosszabb egészségi állapottal rendelkeznek, mint a kritikus szint alattiak, de minél idősebb személyről van szó, a „beesés” annál látványosabb magasabb haskörfogat esetén. Illetve az alacsonyabb haskörfogatnál „lassul” a csökkenés.

Azt is láthatjuk, hogy egyébként a korcsoport és haskörfogat amúgy szignifikáns, jelenteni is fogjuk. A parciális hatásnagyságmutatók itt is értelmezhetők úgy, hogy az adott hatások hány százalékát magyarázzák a modell varianciájának. Itt az interakció önmagában közepes hatásnagyságnak számít (mert ω²_p ~ 0,06), és csak a variancia 5,7%-át magyarázza, míg a szignifikáns főhatások 27,6-58,5%-ot magyaráznak.

Mivel ordinális interakcióról van szó, végezhetünk ugyan post-hoc tesztet, de óvatosan értelmezzük, és ki kell egészítsük Simple Main Effects elemzéssel.

Nézzük meg a post-hoc és Simple Main Effect teszteket párhuzamosan:

Fixált/átlagos korcsoport mellett:

Tukey-korrigált post-hoc teszt

Ennek a változónak csupán két szintje volt, így valójában feleslegesen végezzük el ezeket a próbákat, hiszen ha szignifikáns a főhatás, akkor két szint mellett a post-hoc teszt is szignifikáns lesz.

Mindenesetre az eredményeket leolvasva láthatjuk, hogy átlagos korcsoport mellett a haskörfogatok szerint különbség van az egészségpontszámokban, nagy hatásnagysággal.

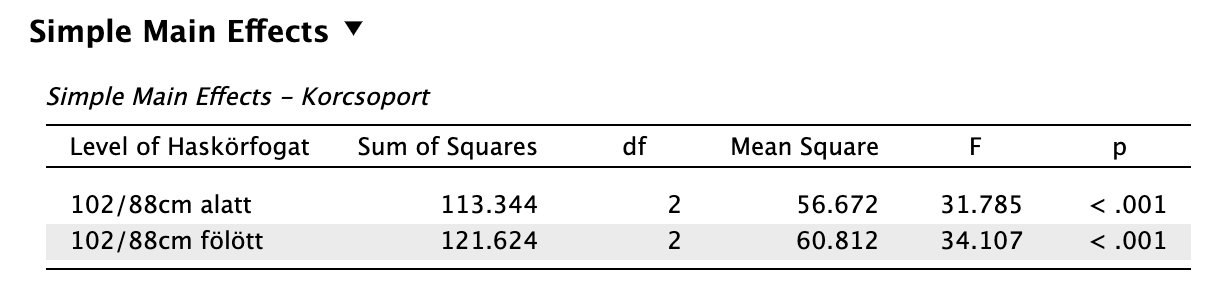
Simple Main Effects

A Simple Main Effects táblából pedig látjuk, hogy korrigálatlan p értékek alapján a változó mindkét szintjén szignifikáns a főhatás. De el kell végeznünk a Holm-féle korrekciót. Két összehasonlítást végeztünk (két szintünk van). Mindkét p értékünket emelkedő sorrendbe kell helyezni, majd kiszámoljuk a megfelelő kritériumszintet (B megközelítés).
- p1 < 0,001 < α = 0,05/2 = 0,025
- p2 < 0,001 < α = 0,05/1 = 0,050 (a 102/88cm alatti a nagyobb, ha kibővítjük a JASP-ban megjelenő tizedeseket)
Tehát Holm-procedúrával korrigált szignifikanciaszint mellett is a haskörfogat változó mindkét szintjén szignifikáns az életkori csoport.
Fixált/átlagos haskörfogat mellett:

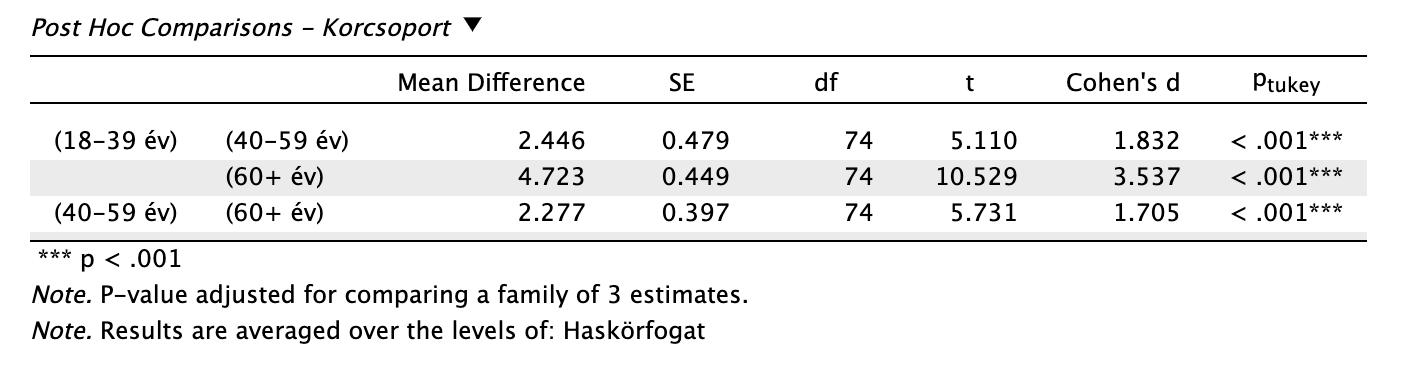
Tukey-korrigált post-hoc teszt

Az eredményeket leolvasva láthatjuk, hogy átlagos haskörfogat mellett az életkori csoportok szerint különbség van az egészségpontszámokban, ismét nagy hatásnagysággal (d).

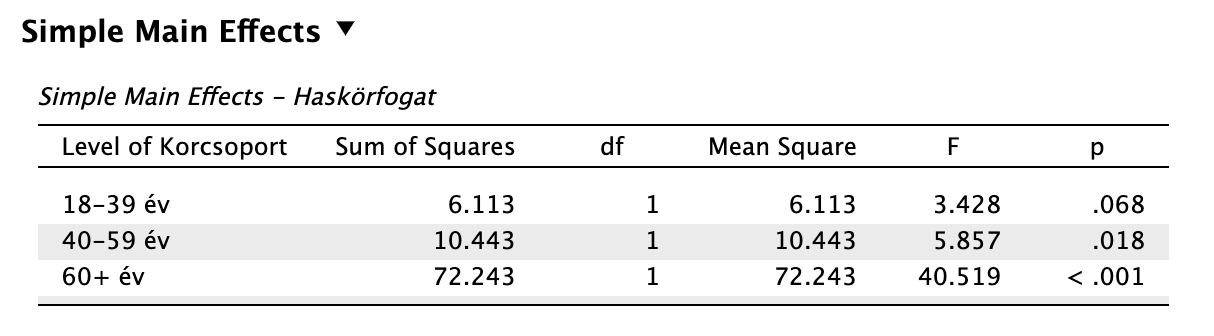
Simple Main Effects

A Simple Main Effects tábla viszont megmutatja, hogy a korcsoportok nem minden szintjén azonos a csökkenő egészség hatás.

Elvégezzük a Holm-procedúrát a p értékeket növekvő sorrendbe helyezve, tudva, hogy 3 összehasonlítást végeztünk.
- p1 < 0,001 < α = 0,05/3 = 0,0167
- p2 = 0,018 < α = 0,05/2 = 0,025
- p3 = 0,068 > α = 0,05/1 = 0,050
Láthatjuk tehát, hogy a legfiatalabb életkori csoport esetén nem beszélhetünk szignifikáns haskörfogat hatásról, 40 és 60 év fölött viszont ez a hatás már szignifikáns.

Példa 14.3 Megoldás. Többszempontos varianciaanalízissel ellenőriztük a haskörfogat (102/88cm alatt vagy fölött) és életkor (18-39, 40-59, 60+ korcsoportok) hatását a fizikai egészségre vonatkozóan. A maradványértékek normalitásának feltétele teljesül a QQ plot szemrevételezése és Shapiro-Wilk próba alapján (W(80) = 0,988, p = 0,682). A szóráshomogenitás feltétele szintén nem sérül a nem szignifikáns Levene-próba eredménye alapján (F(5, 74) = 2,117, p = 0,073).

Statisztikailag szignifikáns, ordinális típusú interakciót találtunk az életkor és haskörfogat között (F(2, 74) = 3,431, p = 0,038, ω²_p = 0,057).

[Illik leírni a főhatásokat akkor is, ha önmagában nem értelmezzük:]

Szignifikáns főhatást találtunk mind a korcsoportok (F(2, 74) = 57,493, p < 0,001, ω²_p = 0,585), mind a haskörfogat (F(1, 74) = 31,505, p < 0,001, ω²_p = 0,276) tekintetében.

A Simple Main Effects utóvizsgálat Holm-korrigált eredményei alapján megállapítható, hogy a haskörfogatnak a legfiatalabb életkori csoportban nincs szignifikáns hatása az egészségi állapotra (p = 0,068), de mindkét idősebb csoportban a hatása statisztikailag szignifikáns. Ezzel szemben az életkor hatása a haskörfogat mindkét szintjére szignifikáns (p < 0,001). Az eredényeket a … táblázat mutatja be:

Egyszerű főhatás	Kontrollváltozó szintje	F	p	Holm-korrigált α
Haskörfogat	18-39 év	3,428	0,068	0,050
	40-59 év	5,857	0,018	0,025
	60+ év	40,519	< 0,001	0,017
Korcsoport	102/88cm alatt	31,785	< 0,001	0,050
	102/88cm fölött	34,107	< 0,001	0,025

Az interakciót a … ábra szemlélteti:

Példa 14.4 (Példa kevert varianciaanalízisre) Kutatásunkban azt vizsgáltuk, hogy mennyire tartós a hatása az egyes terápiás modalitásoknak a rezisztens depresszióra. 8, 16 és 24 hetes utókövetéssel felmértük a depresszió szintjét (összefüggő szempont) három csoportban (független szempont: kontroll, kognitív viselkedésterápia, ketaminasszisztált kognitív viselkedésterápia).

Az adatsor itt letölthető: Rezisztdepr_Factorial_RM.sav

Állítsuk be a vizsgálatot JASP-ban:

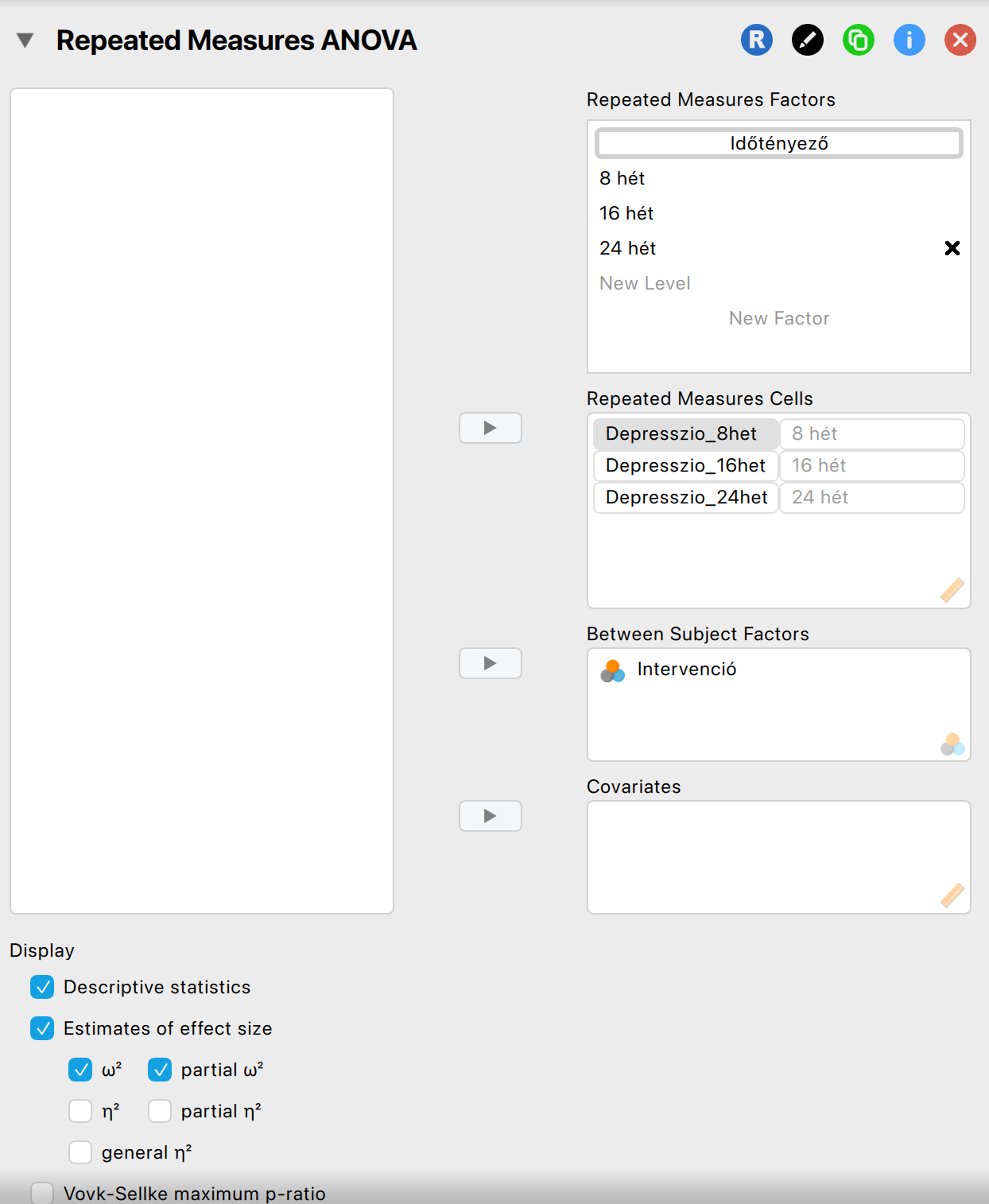
Ellenőrizzük a feltételeket (maradványértékek normál eloszlása, szóráshomogenitás):

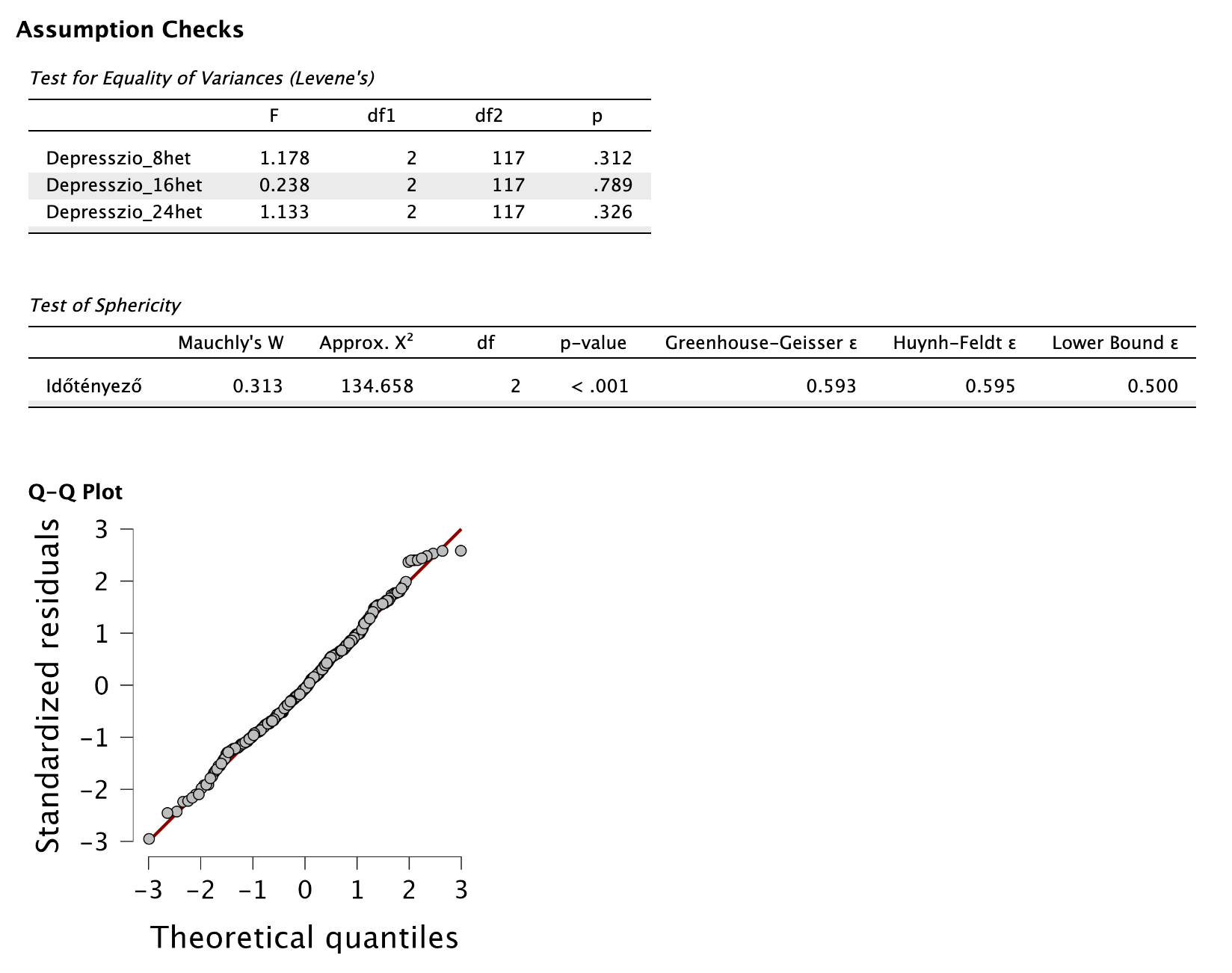
A maradványértékek normalitása QQ plot szemrevételezése alapján teljesül. (A standardizált maradványértékeket új változóként hozzáadva Shapiro-Wilk próbával is tudnánk ellenőrizni a feltétel teljesülését normál ANOVA esetén, de jelenleg a JASP-ban ismételt mérés esetén nem elérhető a funkció.)

A független szempont (három terápiás módozat) szóráshomogenitását a Levene-próbák eredménye igazolja, ami nem szignifikáns (mert p > 0,05), tehát a feltétel teljesül.

Az összefüggő szempont (ismételt mérések) szfericitását a Mauchly-próbával ellenőrizzük. Láthatjuk, hogy a próba szignifikáns, tehát a szfericitás feltétele sérül. Emiatt meg kell vizsgálnunk az ε értéket, és a megfelelő szfericitáskorrekciót alkalmazzuk: mivel a Greenhouse-Geisser ε < 0,75, ezért a Greenhouse-Geisser-korrekciót alkalmazzuk:

A Greenhouse-Geisser-korrigált ANOVA-táblát olvassuk le.

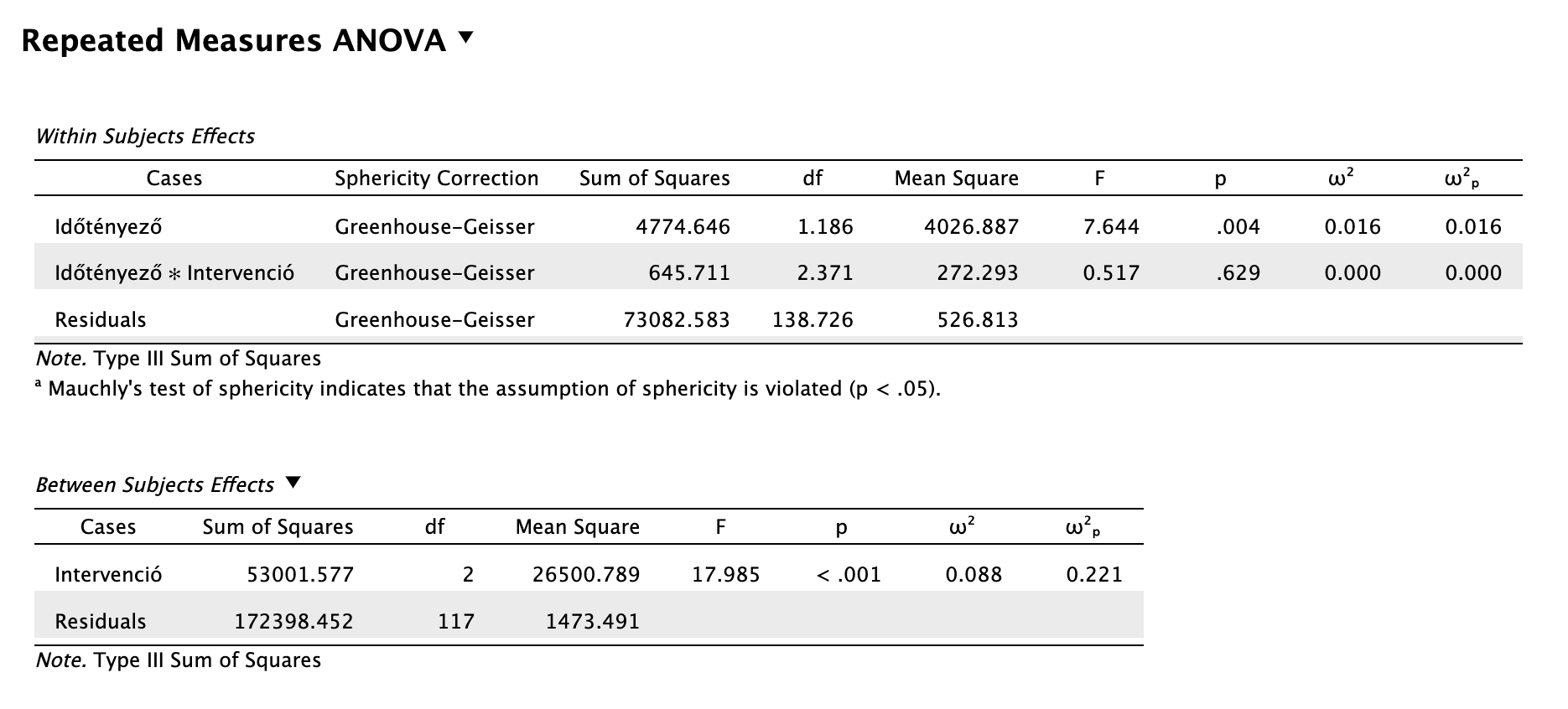
Láthatjuk, hogy két külön ANOVA táblázatunk van. A független szempontra a Between Subjects effects tábla, míg az összefüggő szempontra és az interakcióra a Within Subjects effects tábla.

Létrehozunk egy leíró statisztikai ábrát is, hogy vizualizáljuk az eredményt.

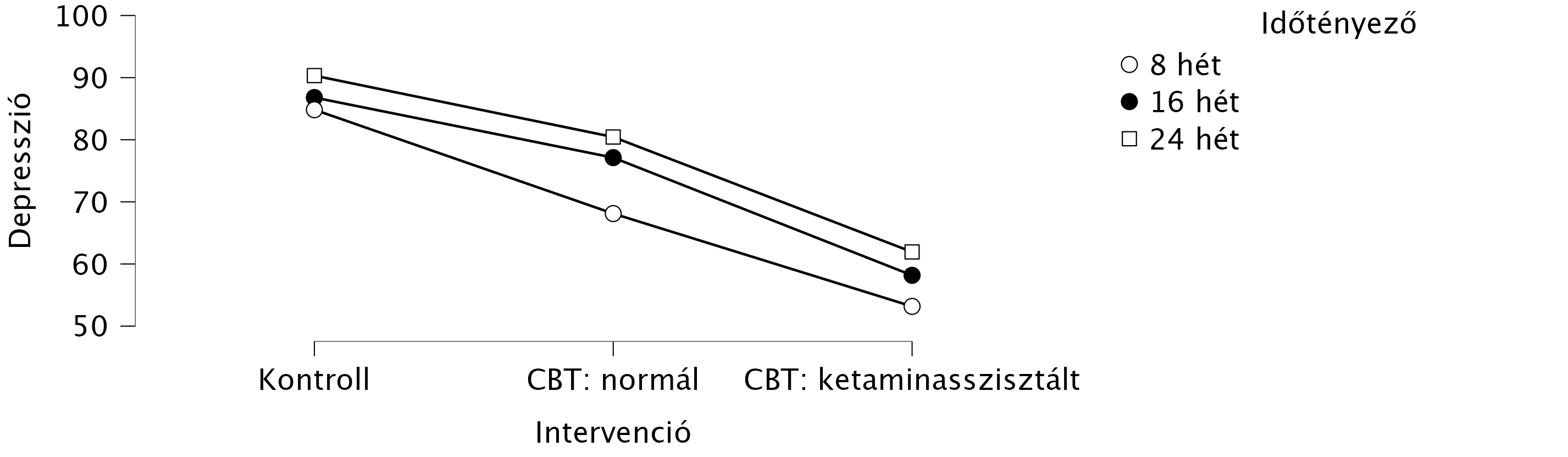
Ahogy minden többszempontos vizsgálatnál, itt is az interakciót olvassuk le először. Láthatjuk, hogy a hatás nem szignifikáns (p = 0,629 > 0,05). Tehát az időtényező és a terápiás módozat hatása nem egymás szintjétől függ. Tehát a főhatásokat önállóan vizsgáljuk, és post-hoc tesztet végzünk Holm korrekcióval az összefüggő szempontra, Scheffé korrekcióval a független szempontra.

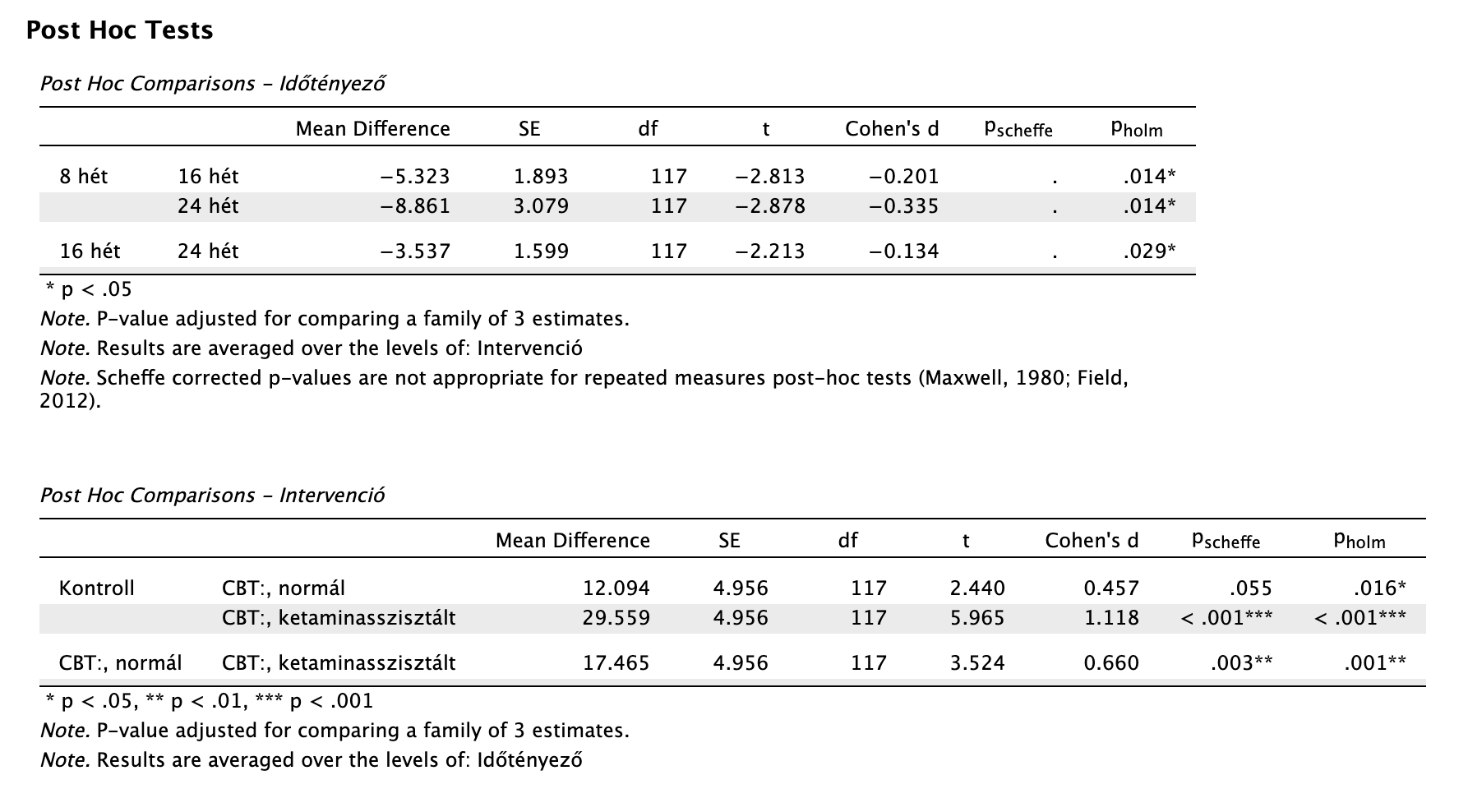
Láthatjuk, hogy a depresszió pontszámok idővel általában visszaemelkednek, de a legerősebb különbség a 8. és 24. hét közötti mérésnél látható (mert Cohen d itt a legnagyobb abszolút értékben, |d| = 0,335). Ennek ellenére minden összehasonlításban szignifikáns a különbség a depresszió szintjében az időpillanatok között „átlagos” terápiás módozat mellett. Az időtényezőnek mint főhatásnak a hatásnagysága kicsi (ω²_p < 0,06).

Az intervenciók közötti főhatás (időpillanattól függetlenül) szintén szignifikáns nagyon nagy hatásnagysággal (ω²_p = 0,221). De a statisztikailag szignifikáns különbség a kontrollcsoport és a ketaminasszisztált kognitív viselkedésterápiás csoport között volt látható (Cohen d = 1,118). Láthatjuk azt is, hogy a Scheffé-korrigált p érték alapján a kontroll és egyszerű CBT módozatok között nincs szignifikáns különbség.

Megoldás 14.2. Kevert mintás varianciaanalízis során ellenőriztük egy longitudinális kísérlet során, hogy mennyire tartós a hatása az egyes terápiás modalitásoknak (CBT és ketaminasszisztált CBT, ill. kontroll) a rezisztens depresszióra három utókövetési időpontban (8, 16, 24 hét). A maradványértékek normál eloszlást követnek a QQ plot szemrevételezése alapján, a Levene-próbák nem szignifikánsak a független szempont egyik szintjén sem (p > 0,05), így a szóráshomogenitás feltétele is teljesül. Az ismételt mérés (összefüggő szempont) szfericitásának ellenőrzésére végzett Mauchly-teszt eredménye szignifikáns (p < 0,001), és a Greenhouse-Geisser mutató (ε = 0,593 < 0,75) értéke alapján Greenhouse-Geisser-féle szfericitáskorrekciót alkalmaztunk az összefüggő szempont értékelésénél.

Az omnibus F-próba alapján a szempontok interakciója nem szignifikáns (F(2,371, 138,726) = 0,517, p = 0,629, ω²_p = 0,000).

Az időtényező mint összefüggő szempont szerinti főhatás statisztikailag szignifikáns kis hatásnagysággal (F(1,186, 138,726) = 7,644, p = 0,004, ω²_p = 0,016). Holm-korrigált post-hoc vizsgálat alapján minden időpillanat között statisztikailag szignifikáns a különbség, tehát igazolható változás állt be a depresszió pontszámok között. A 8-24 hét közötti különbség hatásnagysága a legnagyobb, de kis-közepes mértékű: t(117) = -2,878, p_holm = 0,014, d = -0,335. A 8-16 hetek közötti különbség kisebb: t(117) = -2,813, p_holm = 0,014, d = -0,201; valamint a 16 és 24 hetek között a különbség szintén szignifikáns, de még kisebb, elhanyagolható: t(117) = -2,213, p_holm = 0,029, d = -0,134.

A terápiás módozat mint független szempont szerinti főhatás statisztikailag szignifikáns nagy hatásnagysággal: F(2, 117) = 17,985, p < 0,001, ω²_p = 0,221. A modellünk varianciájának 22%-át magyarázza a terápiás módozat. A Scheffé-korrigált post-hoc vizsgálat alapján az egyszerű CBT intervencióban részesülők és a kontrollcsoport között nem volt statisztikailag szignifikáns különbség: t(117) = 2,440, p_scheffe = 0,055, d = 0,457. Nagy hatásnagyságú, szignifikáns különbség volt a kontrollcsoport és a ketaminasszisztált CBT csoport depressziópontszámaiban az utókövetés során: t(117) = 5,965, p_scheffe < 0,001, d = 1,118. Az egyszerű és ketaminasszisztált kognitív viselkedésterápia között is szignifikáns, közepes hatásnagyságú különbséget találtunk: t(117) = 3,524, p_scheffe = 0,003, d = 0,660.

A különbségeket a … ábra szemlélteti:

[Megjegyzés: A Scheffé korrekció a legkonzervatívabb, amit az ANOVA feltételeinek sérülésekor alkalmazunk. Tukey-korrekcióval a Kontroll és egyszerű CBT közütti különbség már pont szignifikáns. Érdemes a diszkusszióban kitérni erre.]