11 Páros vagy összefüggő mintás elrendezés
Az összefüggő mintás vagy párosmintás elrendezés lényege, hogy egy adott csoportot vizsgál két különböző helyzetben (pl. különböző kísérleti elrendezésben) vagy két különböző időpontban (pl. intervenció előtt vagy után). A kérdése, hogy van-e különbség csoporton belül két különböző időpontban / helyzetben? Ez az úgynevezett within-subjects vizsgálati helyzet.
Az összefüggő mintás próba hipotézisei:
- H0: A két időpontban / helyzetben mért átlag egyenlő
Kétoldalú próba esetén:
- H1: A két időpontban / helyzetben mért átlag nem egyenlő
Egyoldalú próba esetén:
- H1: Egyik időpontban/helyzetben mért átlag kisebb, mint a másik időpontban/helyzetben mért átlag
VAGY
- H1: Egyik időpontban/helyzetben mért átlag nagyobb, mint a másik időpontban/helyzetben mért átlag
11.1 Összefüggő (páros) mintás t-próba
Az összefüggő mintás t-próba feltételei:
- A függő változó skála típusú
– A minták összetartoznak
– Az mintaelemek különbségeinek eloszlása megközelítőleg normál eloszlású
Amennyiben a változónk nem követik a normál eloszlást, úgy Wilcoxon előjeles rangpróbát1 futtatunk.
Példa 11.1 Kutatásunkban egészségpszichológiai intervenciót (20 alkalmas CBT terápiás csoport) alkalmazunk testsúlycsökkentés céljából (N =) 40 fő részvételével. Vizsgáljuk meg, hogy sikeres volt-e az intervenció.
Az adatokat ez a letölthető adatfájl tartalmazza: CBT_testsuly.sav
Vizsgáljuk meg a feltételek teljesülését!
A függő változó skála típusú
Igen, mert testsúlyt mérünk, ami skálaváltozó.
A minták összetartoznak
Igen, ugyanazokkal az embereket mértük fel két különböző időpontban.
Az mintaelemek különbségeinek eloszlása megközelítőleg normál eloszlású
Erre a párosmintás t próba modulba épített előztetes normalitásvizsgálatot (Shapiro-Wilk tesztet alkalmazzuk).
A próba beállítása JASP-ban:
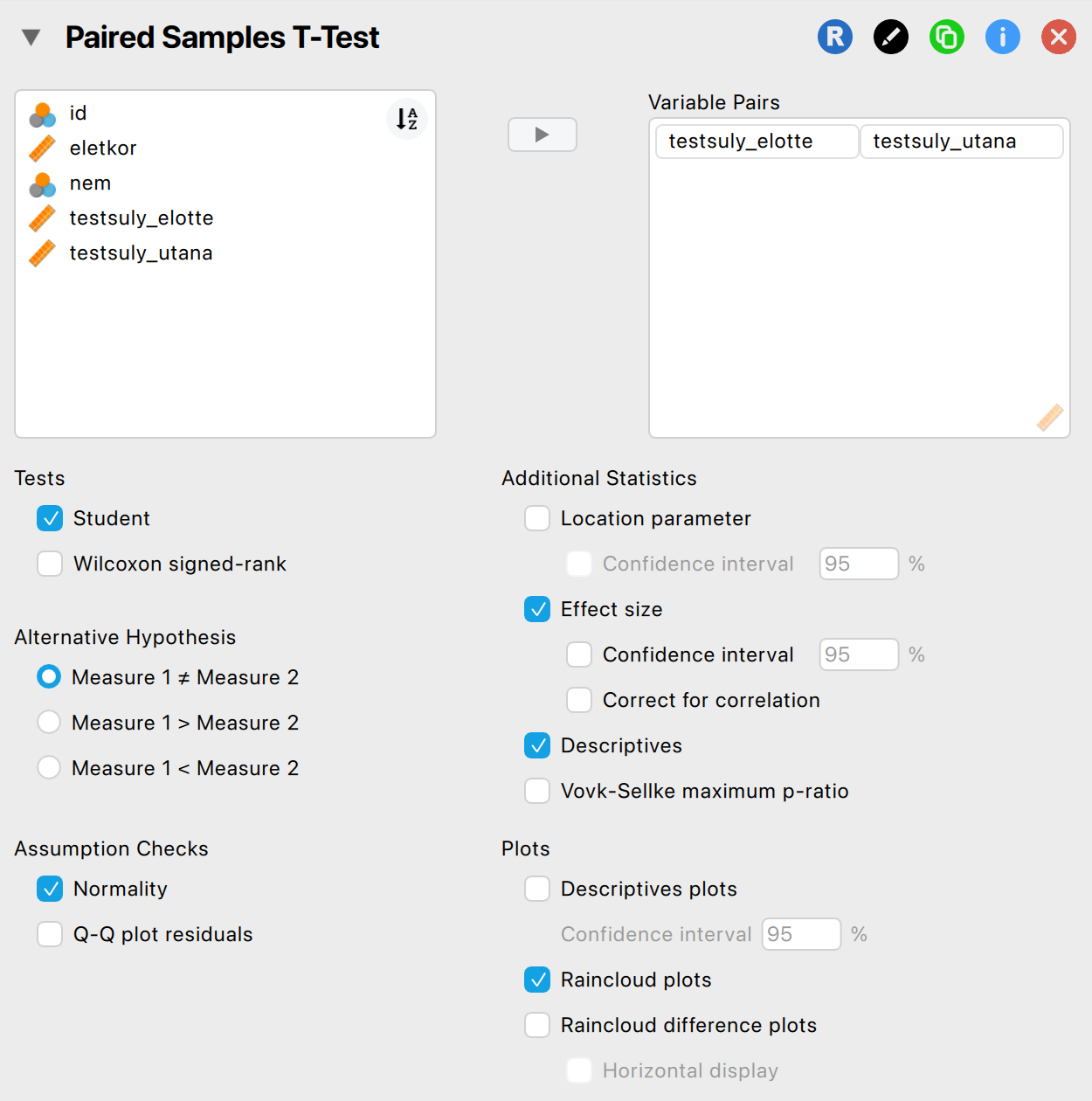
A próba eredményeinek leolvasása
Előzetes normalitásvizsgálat

Az mintaelemek különbségeinek eloszlása megközelítőleg normál eloszlású, mert a Shapiro-Wilk próba eredménye nem szignifikáns (p > 0,05).
A próba eredményei:

A JASP a megjegyzések között jelzi nekünk, hogy Student-féle t-próbát végzünk (a páros formát).
A t-próba t-statiszikája: 7,363. Hogyan jött ki?
A szabadságfok: 39. Ez a mintaelemszámnál eggyel kisebb érték, vagyis \(N\) - 1.
A p-érték: < 0,001. A próba szignifikáns, mert \(p < 0,05\). Hogyan jött ki?
A Cohen-d hatásnagyság: 1,164. Ez Cohen (1988) alapján nagy hatásnagyság.
A csoportok átlagát és szórását az eredmények közlésekor le kell írni. Ehhez nem szükséges elnavigálni, a t-próbáknál a Descriptives kipipálásával a szükséges leíró statisztikák előállnak:
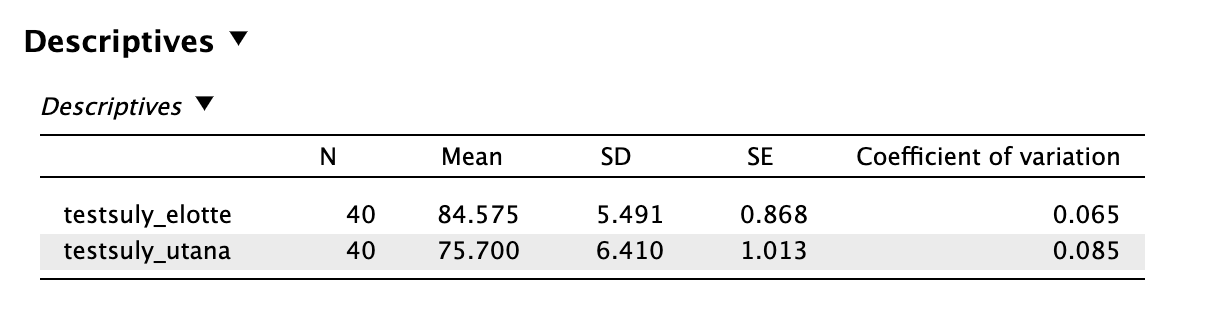
Egy boxplotpár és sűrűségfüggvény-pár kombinációját tartalmazó ábrát készíthetünk a JASP segítségével a modulon belül a Raincloud plots funkció kipipálásával:
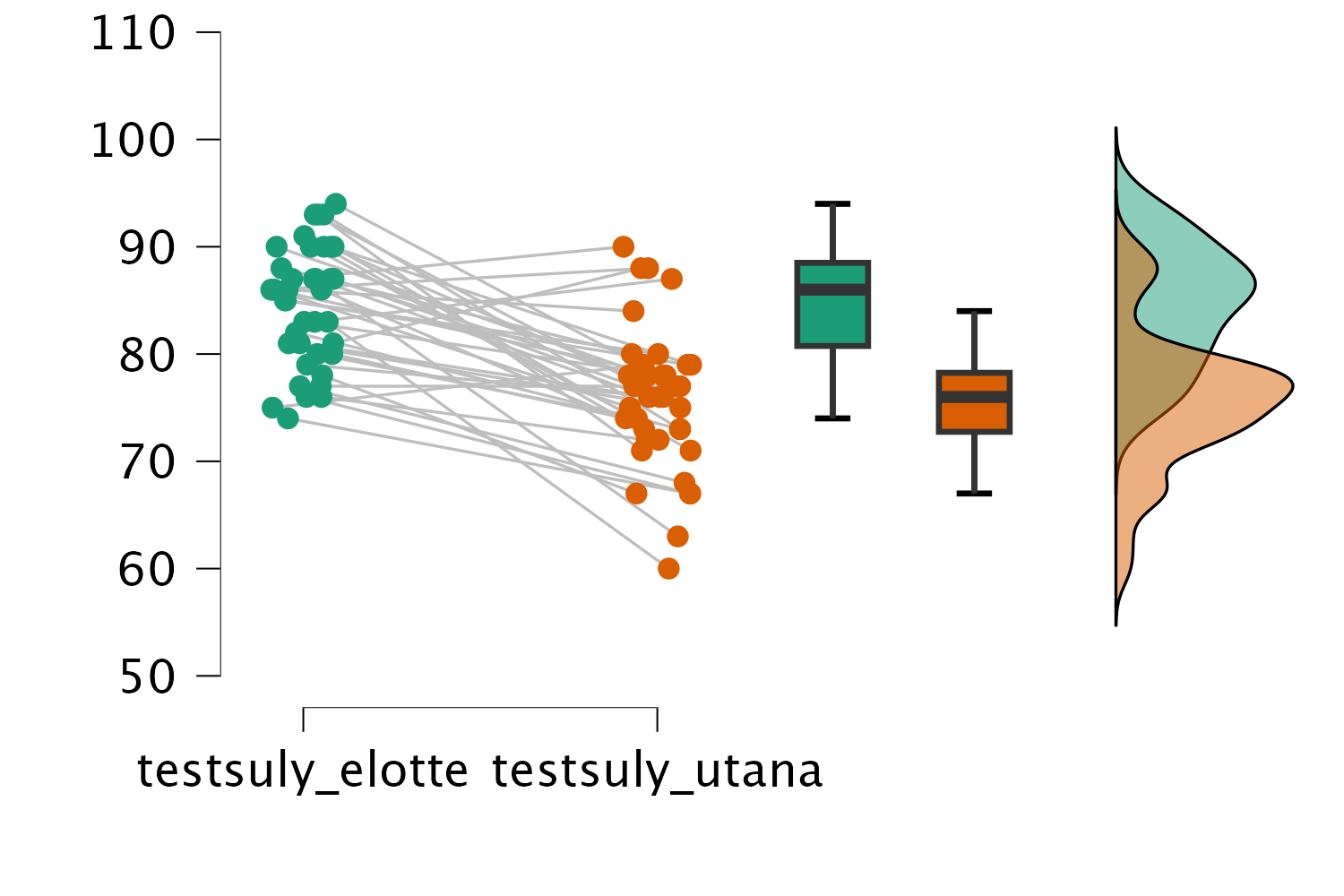
Láthatjuk az átlagos testsúlycsökkenést, de észrevehetjük, hogy voltak olyanok is, akiknek nőtt a testsúlyuk az intervenció alatt.
Megoldás 11.1. A 20 alkalmas testsúlycsökkentési célú CBT terápiás intervenciónk sikerességének ellenőrzésére párosmintás t-próbát végeztünk az intervenció előtt és azt követően felmért testsúly adatok alapján. Az adatok normál eloszlást követtek (W(40) = 0,979, p = 0,656), így a Student-féle páros mintás t-próbát végeztük el.
Az átlagos testsúly intervenció előtt (M =) 84,50 kg volt (SD = 5,49), és intervenciót követően (M =) 75,70 kg-ra (SD = 6,41) csökkent. A különbség statisztikailag szignfikáns és nagy hatásnagyságú: t(39) = 7,363, p < 0,001, d = 1,164.
Kiegészítés 11.1 (A páros mintás Student-féle t-próba t-értékének kiszámítása). \[ t = \frac{\bar{D}}{ \frac{s}{\sqrt{n}} } \]
ahol:
- \(\bar{D}\) az elemek csoportközi különbségének átlaga
- \(\frac{s}{\sqrt{n}}\) pedig a standard hiba
Kiegészítés 11.2 (A párosmintás t-próba p-értékének kiszámítása). A kiszámított t-próba értékének a valószínűségét kiszámítjuk adott szabadságfokú (df) t-eloszláson.
Kétoldalú próba esetén
\[ p = 2 \times P(T > |t|) \]
Egyoldalú próba esetén \[ p = P(T > |t|) \]
VAGY
\[ p = P(T < |t|) \]
11.2 Összefüggő (páros) mintás nemparametrikus próba: Wilcoxon előjeles rangpróba
Amennyiben a különbségek nem követik a normál eloszlást, nem alkalmazhatjuk a Student-féle t-próbát, helyette ismét rangpróbát alkalmazunk, ahogy a korábbi fejezetekben is láthattuk.
A Wilcoxon előjeles rangpróba hipotézisei kétoldalú próba esetén:
- H0: a két összetartozó minta különbségének mediánja nulla
- H1:a két összetartozó minta különbségének mediánja nem nulla
Hatásnagysága szintén nem távolságjellegű mutató (d), hanem rangbiszeriális korrelációs együttható, tehát az értelmezésénél a korrelációs együtthatók értelmezését kell figyelembe venni.
Példa 11.2 Kutatásunkban egészségpszichológiai intervenciót (20 alkalmas CBT terápiás csoport) alkalmazunk testsúlycsökkentés céljából (N =) 40 fő részvételével. Vizsgáljuk meg, hogy sikeres volt-e az intervenció.
Az adatokat ez a letölthető adatfájl tartalmazza: CBT_testsuly_nonnormal.sav
Vizsgáljuk meg a feltételek teljesülését!
A függő változó skála típusú
Igen, mert testsúlyt mérünk, ami skálaváltozó.
A minták összetartoznak
Igen, ugyanazokkal az embereket mértük fel két különböző időpontban.
Az mintaelemek különbségeinek eloszlása megközelítőleg normál eloszlású
Erre a párosmintás t próba modulba épített előztetes normalitásvizsgálatot (Shapiro-Wilk tesztet alkalmazzuk).
A próba beállítása JASP-ban:
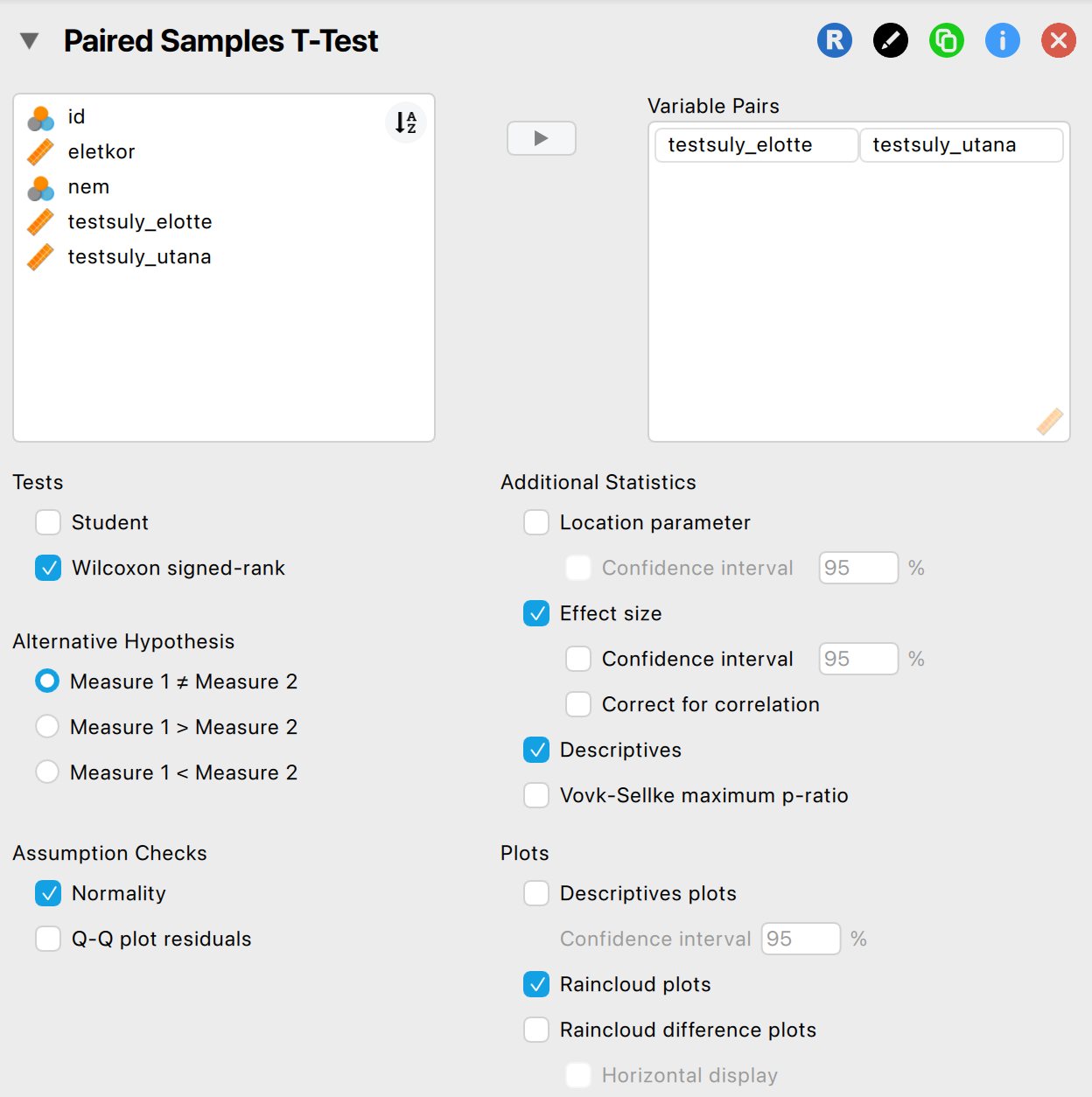
A próba eredményeinek leolvasása
Előzetes normalitásvizsgálat

Az mintaelemek különbségeinek eloszlása nem normál eloszlású, mert a Shapiro-Wilk próba eredménye szignifikáns (p < 0,05).
A próba eredményei:

A JASP a megjegyzések között jelzi nekünk, hogy Student-féle t-próbát végzünk (a páros formát).
A próba W mutatója: 819,000. Ez a rangösszegeket mutatja meg. Hogyan jött ki?
A próba z-statisztikája: 5,497. Ezt hivatkozzuk majd. Hogyan jött ki?
A p-érték: < 0,001. A próba szignifikáns, mert \(p < 0,05\). Hogyan jött ki?
A rangbiszeriális hatásnagyság: 0,998. Ez Cohen (1988) alapján nagy hatásnagyság.
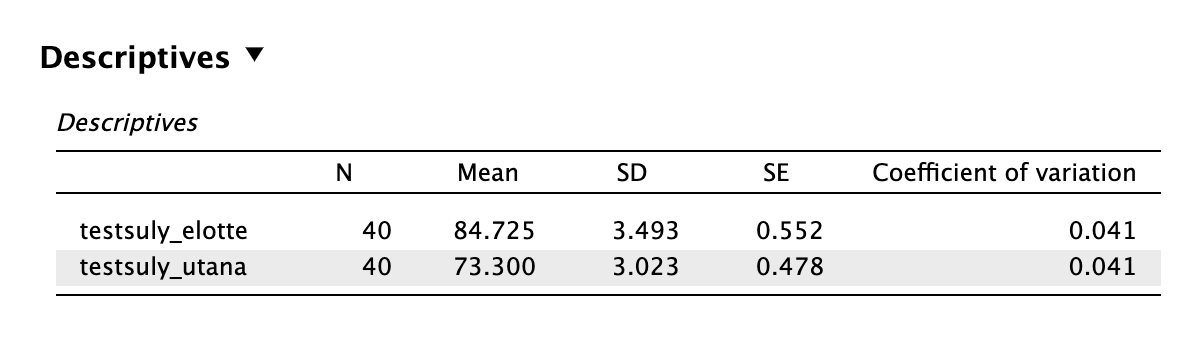
A csoportok átlagát és szórását az eredmények közlésekor le kell írni. Ehhez nem szükséges elnavigálni, a t-próbáknál a Descriptives kipipálásával a szükséges leíró statisztikák előállnak:
Egy boxplotpár és sűrűségfüggvény-pár kombinációját tartalmazó ábrát készíthetünk a JASP segítségével a modulon belül a Raincloud plots funkció kipipálásával:
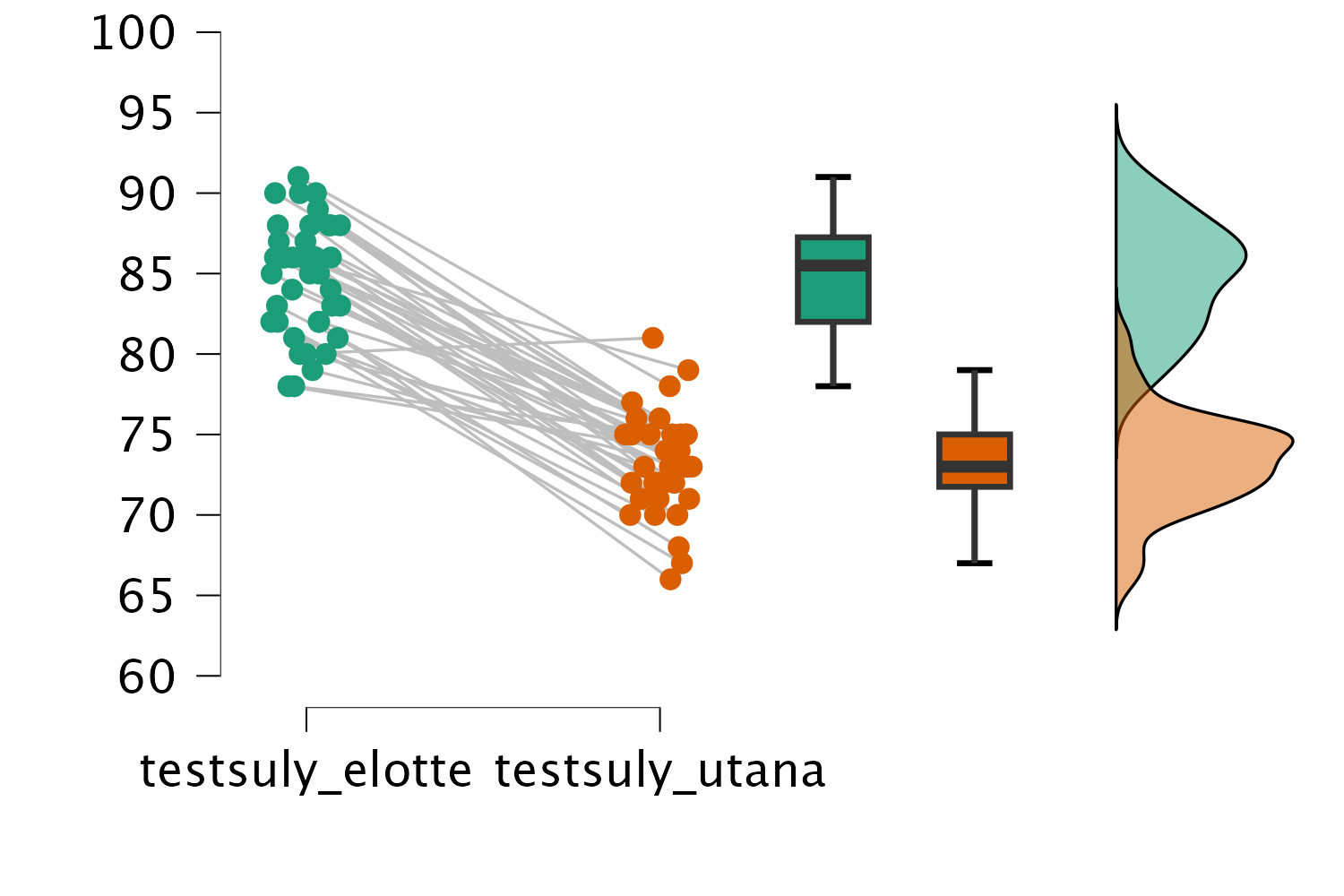
Láthatjuk az átlagos testsúlycsökkenést, de észrevehetjük, hogy voltak olyanok is, akiknek nőtt a testsúlyuk az intervenció alatt.
Megoldás 11.2. A 20 alkalmas testsúlycsökkentési célú CBT terápiás intervenciónk sikerességének ellenőrzésére párosmintás t-próbát végeztünk az intervenció előtt és azt követően felmért testsúly adatok alapján. Az adatok nem követik a normál eloszlást (W(40) = 0,920, p = 0,007), ezért a Wilcoxon előjeles rangpróbát végeztük el.
Az átlagos testsúly intervenció előtt (M =) 84,73 kg volt (SD = 3,49), és intervenciót követően (M =) 73,30 kg-ra (SD = 3,02) csökkent. A különbség statisztikailag szignfikáns és nagy hatásnagyságú: z = 5,497, p < 0,001, rrb = 0,998.
Kiegészítés 11.3 (A párosmintás Wilcoxon előjeles rangpróba W és z értékei). W statisztika:
A csoportok/minták közötti különbségek abszolút értékéből nyersrangokat képzünk. Egyenlőség esetén átlagoljuk a rangokat. Ezt követően az eredeti különbségek előjele alapján csoportosítjuk a pozitív és negatív rangokat. A pozitív rangokat összegezzük, ez lesz a W statisztika.
Elemszám alapján kiszámítjuk a W várható értékét (uW): \[ u_W = \frac{n \times (n+1)}{4} \]
Kiszámítjuk a szórást elemszám és páros rangok alapján:
\[ s_W = \sqrt{ \frac{n \times (n+1) \times (2n+1) - \sum_{i=1}^k{\frac{t_i^3-t_i}{2}}}{24} } \]
A z statisztika kiszámítása
\[ z = \frac{W-u_W}{s_W} \]
Kiegészítés 11.4 (A párosmintás Wilcoxon előjeles rangpróba p-értékének kiszámítása). A kiszámított z-statisztika értékének a valószínűségét kiszámítjuk egy z-eloszláson.
Kétoldalú próba esetén
\[ p = 2 \times P(Z ≤ -|z|) \]
Nem keverendő a függetlenmintás Wilcoxon rangösszeg próbával!↩︎