| Statistic | FELNE8 |
|---|---|
| N | 118.000 |
| Missing | 0.000 |
| Mean | 21.881 |
| SE (Mean) | 0.497 |
| SD | 5.404 |
| SE (SD) | 0.353 |
| Variance | 29.199 |
| SE (Var) | 3.818 |
| Median | 22.000 |
| Min | 9.000 |
| Max | 32.000 |
| IQR | 7.000 |
| Q1 (25%) | 18.000 |
| Q3 (75%) | 25.000 |
| Skewness | -0.146 |
| SE (Skew) | 0.223 |
| Kurtosis | -0.515 |
| SE (Kurt) | 0.442 |
| Shapiro W | 0.984 |
| Shapiro p | 0.166 |
10 Függetlenmintás elrendezés két minta esetén
Már az egymintás próbák során is megjelent a függetlenség mint előfeltétel. Ebben a fejezetben is független mintákkal dolgozunk.
A fejezetben bemutatott eszközök a következő kérdések megválaszolásában segíthetnek:
- van-e különbség a vizsgált változó tekintetében két csoport/minta között?
- van-e különbség két csoport vagy kísérleti helyzet között, ahol a résztvevők mindkét csoportban különbözőek?
Ez az elrendezés az úgynevezett between-subjects elrendezés.
Példa 10.1 Az előző fejezetben megismert kísérlet módosított változatával folytatjuk.
Készítettünk egy kérdőíves vizsgálatot a szociális szorongásról, amelyben a Félelem a negatív megítéléstől kérdőív (Watson & Friend, 1969) legrövidebb, 8 itemes, magyar változatát (Perczel-Forintos & Kresznerits, 2017) használtuk általános és klinikai populáción, mely jó belső konzisztenciával rendelkezik (Cronbach \(\alpha\) = 0,837) és nem, életkor, végzettség és szocioökonómiai státusz tekintetében nem különbözik a hosszú változattól.
A kérdőíves adatainkban jelöltük, ha a válaszadó rendelkezik F32.XX Depressziós epizód BNO kódú diagnózissal vagy F40.10 Szociális fóbia BNO kódú diagnózissal.
A minta főbb mutatói a FÉLNE-8 összpontszámokra vonatkozóan:
F32.XX kódú diagnózissal rendelkezők gyakorisági táblája:
| BNO | N | Relatív gyakoriság |
|---|---|---|
| Igen | 27 | 22.9% |
| Nem | 91 | 77.1% |
F4010 kódú diagnózissal rendelkezők gyakorisági táblája:
| BNO | N | Relatív gyakoriság |
|---|---|---|
| Igen | 35 | 29.7% |
| Nem | 83 | 70.3% |
Az adatfájl letölthető: FELNE8_pelda.sav
Megoldás 10.1. A vizsgálatban (N =) 118 fő vett részt, közülük 68 nő (57,6%) és 50 férfi (42,4%). A vizsgált személyek átlagéletkora (M =) 35,16 év (SD = 2,99). A mintában a szociális szorongás (FÉLNE-8) átlagpontszáma (M =) 21,88 (SD = 5,40). A változó normál eloszlást követ (W(118) = 0,984, p = 0,166). A mintában 35 fő szociális fóbiával, és 27 fő major depresszióval diagnosztizált személy; kettős diagnózissal 10 fő rendelkezik.
10.1 Függetlenmintás t-próbák: Student-féle t-próba
A különbségek vizsgálatára t-próbát végezhetünk a független csoportok/helyzetek között. Student-féle t-próba vagy Welch-féle t-próba közül válaszhatunk, ezek közül a Student-féle t-próbának szigorúbb feltételei vannak.
A Student-féle t-próba feltételei:
- A függő változó skála típusú
- A csoportok/minták függetlenek egymástól
- A függő változó megközelítőleg normál eloszlású csoportonként
- A csoportok varianciája közel azonos (fennáll a szóráshomogenitás)
Definíció 10.1 (szóráshomogenitás) (equality of variances, homogeneity of variance)
A vizsgált függő változó szórása (varianciájának négyzetgyöke) megegyezik az összehasonlítandó két csoportban.
A szóráshomogenitás fogalma a regressziós modellek esetén a homoszkedaszticitás, hiánya, vagyis nem teljesülése a heteroszkedaszticitás.
A Welch-féle t-próbát alkalmazzuk abban az esetben, ha a szóráshomogenitás feltétele nem teljesül.
A t-próba feltételeinek ellenőrzését a következőképpen végezzük:
A függő változó skála típusú
Erről meggyőződünk.
A csoportok/minták függetlenek egymástól
Erről a kísérleti elrendezés biztosít minket.
A függő változó megközelítőleg normál eloszlású csoportonként
Itt nem lesz elegendő, hogy egyszerű Shapiro-Wilk próbát futtatunk a vizsgált változó egészére, hanem csoportonkénti bontásban (JASP-ban: split) kell elvégeznünk a vizsgálatot.
Erre lehetőségünk van a már jól ismert Descriptive Statistics modulban, vagy a függetlenmintás t-próba modulban (Independent Samples T-Test). Ez utóbbit javaslom, mert a szóráshomogenitás vizsgálatát is itt végezzük el.
A függetlenmintás t-próba modulban elegendő az Assumption Checks rovatban a Normality vizsgálat kipipálása, hogy a JASP kiszámolja a csoportonkénti normalitás kombinált mutatóját.
A csoportok varianciája közel azonos (fennáll a szóráshomogenitás)
A feltétel ellenőrzését a Levene-próbával vagy a Brown-Forsythe-próbával végezzük JASP-ban.
A Levene-próba feltétele, hogy az összehasonlítandó csoportok közel azonos méretűek legyenek (ti. illesztettek) és a vizsgált változó normál eloszlású legyen. Ha ezen feltétel közül legalább az egyik nem áll fenn, akkor egy robusztus próbát, a Brown-Forsythe-próbát kell alkalmaznunk, mely esetben nem kell a csoportok illesztettek legyenek és/vagy a vizsgált változó nem kell normál eloszlást kövessen.
A függetlenmintás t-próba modulban Assumption Checks rovatában az Equality of variances vizsgálatot pipáljuk be, és választunk a két próba közül.
Ha a próbák eredménye szignifikáns (p < 0,05), akkor a szóráshomogenitás feltétele nem teljesül. Ha a próbák eredménye nem szignifikáns (p > 0,05), akkor a szóráshomogenitás feltétele teljesül.
Példa 10.2 (Példa Student-féle t-próbára nem illesztett minta esetén) Szeretnénk megtudni, hogy az általunk mért félelem a negatív megítéléstől átlagpontszám (FÉLNE-8) különbözik-e a major depresszióval (F32.XX) diagnosztizáltak és nem diagnosztizáltak között.
Állítsuk fel a hipotézisünket!
Nullhipotézis (H0): A depresszióval diagnosztizáltak és depresszióval nem diagnosztizáltak FÉLNE-8 pontszámon mért csoportátlaga megegyezik. Alternatív hipotézis (H1): A depresszióval diagnosztizáltak és depresszióval nem diagnosztizáltak FÉLNE-8 pontszámon mért csoportátlaga eltér.
Vizsgáljuk meg az előfeltételeket!
A függő változó skála típusú?
Igen, Likert skálával mért itemek összpontszámáról van szó, így intervallumskálaként kezelhető változó.
A csoportok függetlenek egymástól?
Igen, nem lehet valaki egyszerre depresszióval diagnosztizált és nem diagnosztizált.
A függő változó megközelítőleg normál eloszlású csoportonként?
Ezt a JASP-ban ellenőrizzük a függetlenmintás t-próba modul Assumption Checks rovatában a Normality vizsgálat kipipálásával.
A csoportok varianciája közel azonos (fennáll a szóráshomogenitás)?
Ezt is a JASP-ban ellenőrizzük a függetlenmintás t-próba modul Assumption Checks rovatában az Equality of variances vizsgálat bepipálásával. Azonban el kell döntenünk, hogy az összehasonlítandó minták (csoportok) közel azonos nagyságúak-e.
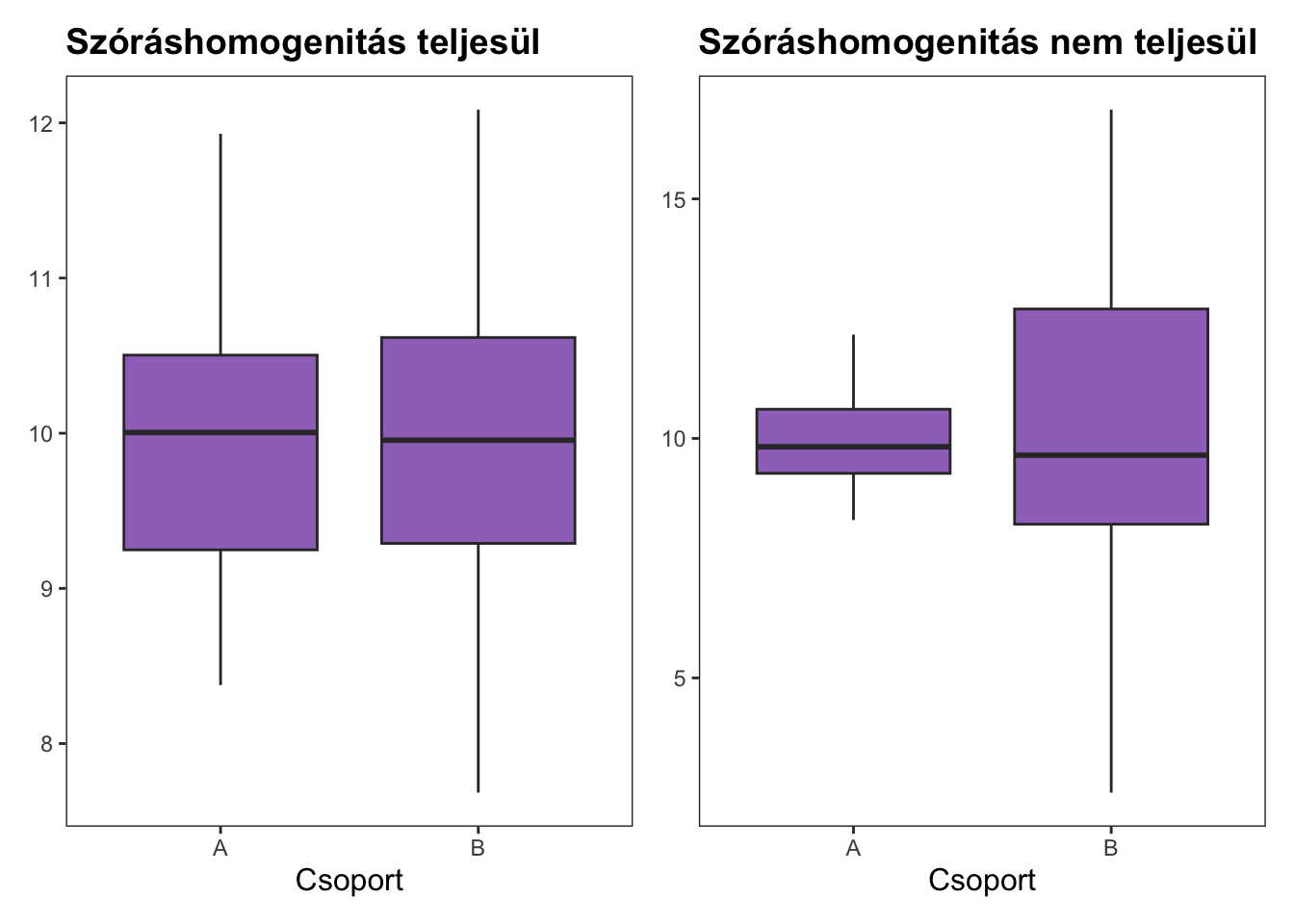
Szemrevételezzük újra az adatsorunk megismerésekor létrehozott gyakorisági táblát (amit magunk is létre tudunk hozni a JASP-ban a már ismert módon).
Láthatjuk, hogy a százalékos megoszlás messze elmarad az 50-50%-tól, tehát a minták nem illesztettek, ezért a Levene-próba helyett a Brown-Forsythe-próbát választjuk ki.
Állítsuk be a vizsgálatot JASP-ban!
Olvassuk le és értelmezzük az eredményeket!
Normalitásvizsgálat eredménye
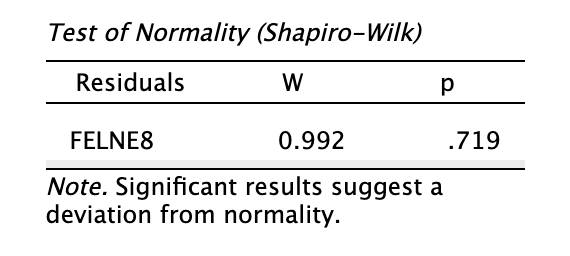
Láthatjuk, hogy a Shapiro-Wilk próba eredménye nem szignifikáns (p > 0,05), tehát a változó csoportonként követi a normál eloszlást.
Szóráshomogenitás-vizsgálat eredménye

A Brown-Forsythe-próba eredménye nem szignifikáns (p > 0,05), tehát a csoportok varianciája és szórása közel azonos, a Student-féle t-próba elvégezhető.
A Student-féle t-próba eredménye.
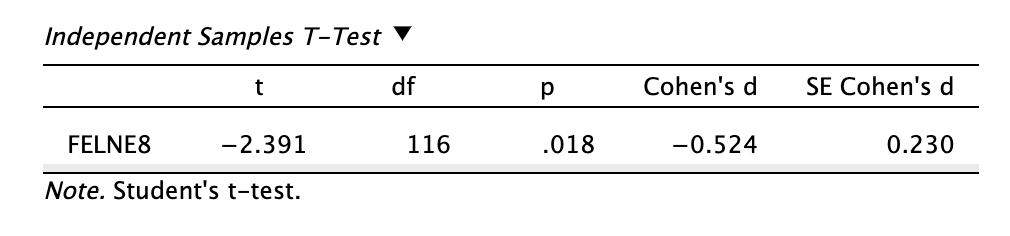
A JASP a megjegyzések között jelzi nekünk, hogy a lehetséges t-próbák közül a Student-féle t-próbát végezzük („Student’s t-test”).
A t-próba t-statiszikája: -2,391. Hogyan jött ki?
A szabadságfok: 116. Ez a két csoport elemszámánál kettővel kisebb érték: n1 + n2 - 2.
A p-érték: 0,018. A próba szignifikáns, mert \(p < 0,05\). Hogyan jött ki?
Cohen-d hatásnagyság: -0,524. Ez Cohen (1988) alapján közepes hatásnagyság.
Az összehasonlítandó csoportátlagokat és mögöttes eloszlásokat az alábbi ábra szemlélteti:
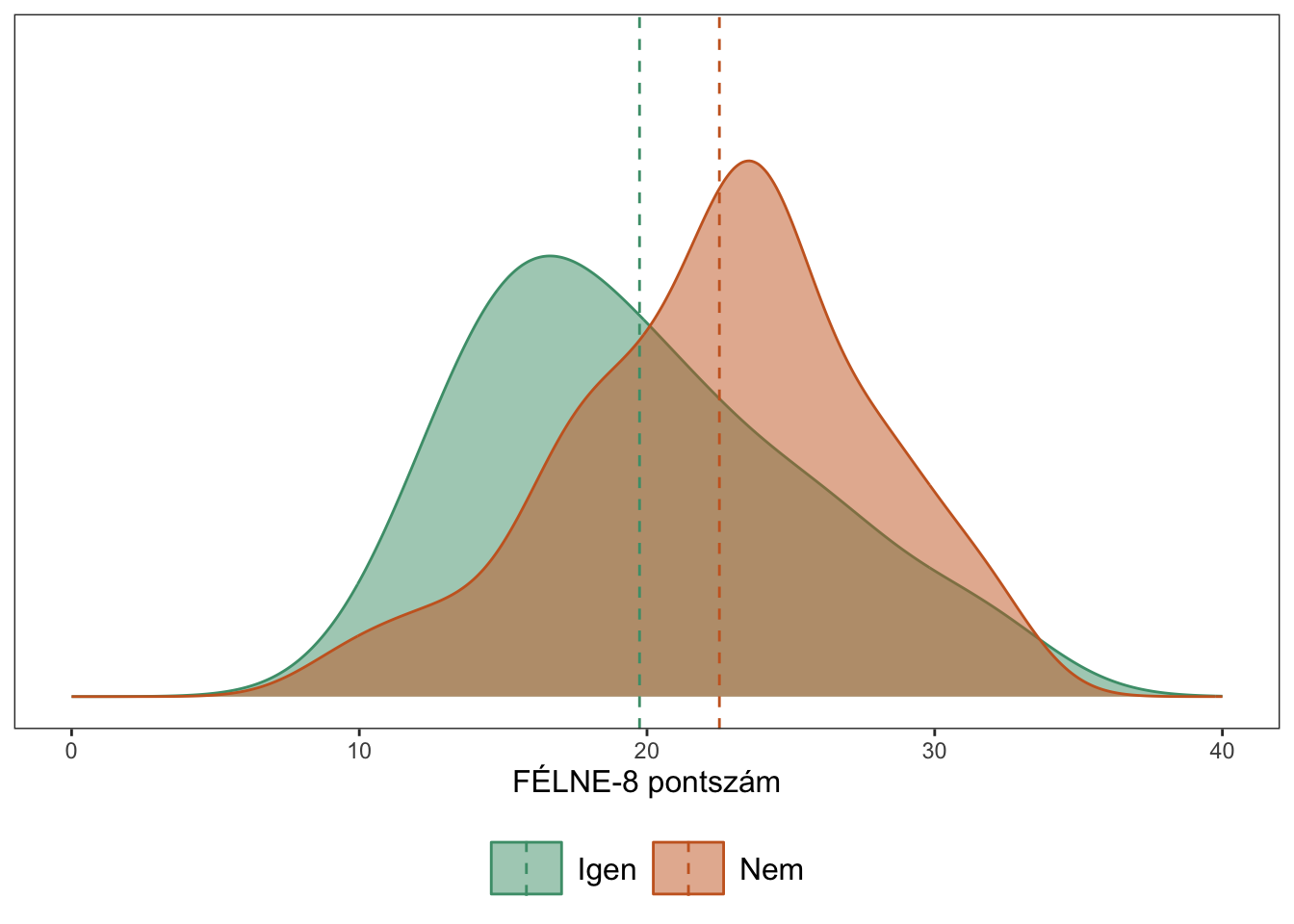
Egy boxplotpár és sűrűségfüggvény-pár kombinációját tartalmazó ábrát magunk is készíthetünk a JASP segítségével a modulon belül a Raincloud plots funkció kipipálásával. Az alapértelmezett ábra így fog kinézni:
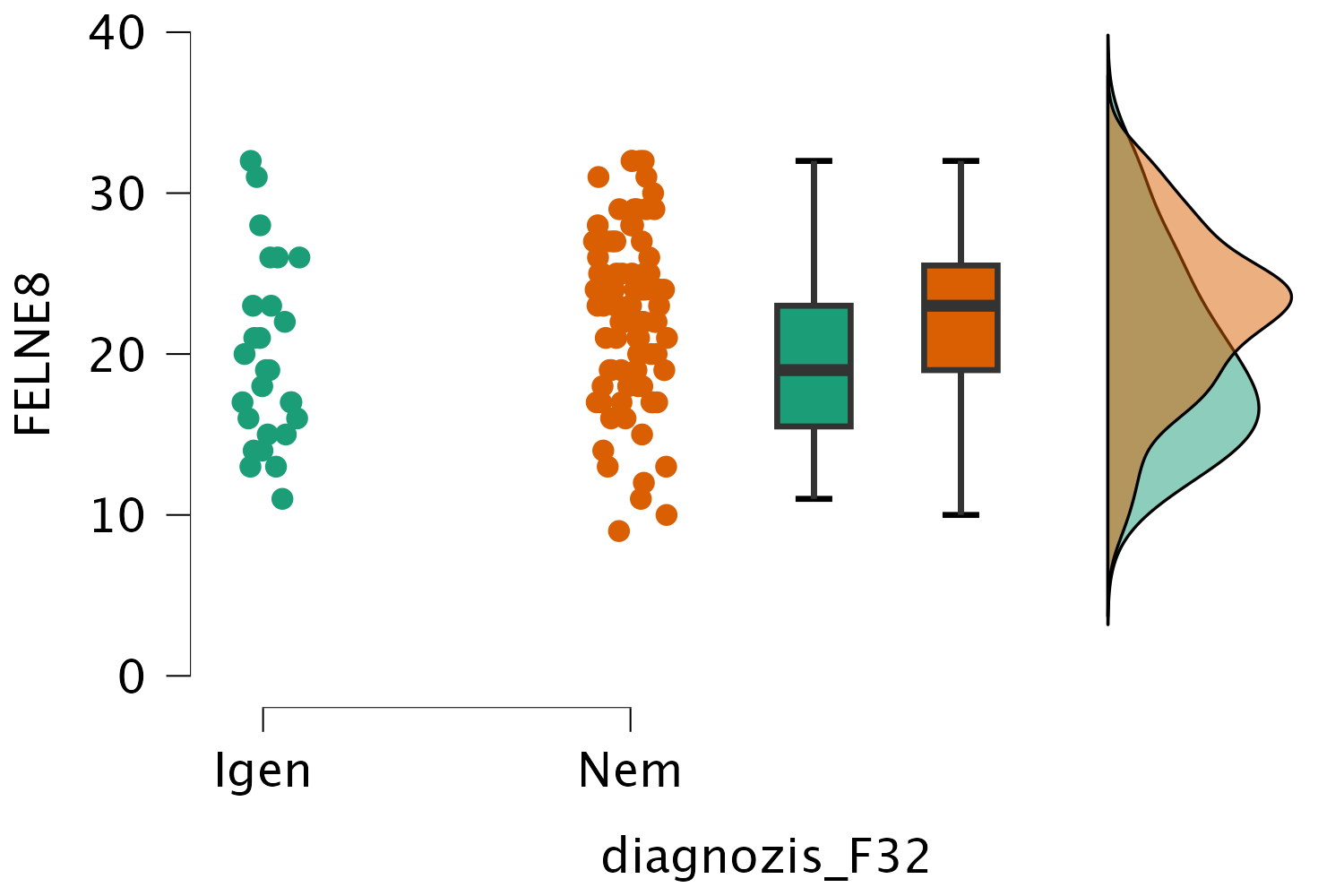
Ha szeretnénk, „horizontális” formát is válaszhatunk, ez esetben egymás alatt jelennek meg a sűrűségfüggvények, a boxplotok pedig vízszintesen:
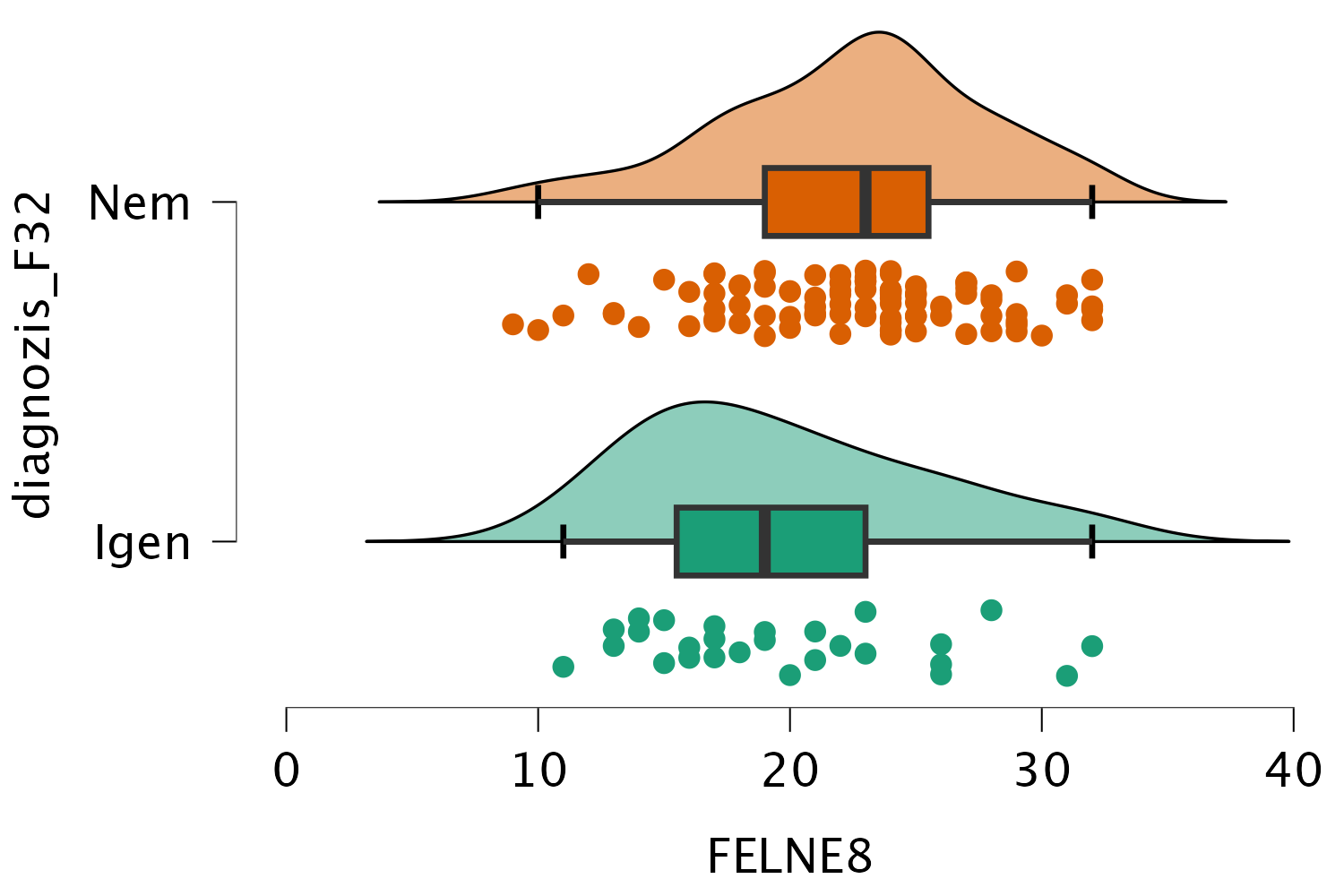
A csoportok átlagát és szórását az eredmények közlésekor le kell írni. Ehhez nem szükséges elnavigálni, a t-próbáknál a Descriptives kipipálásával a szükséges leíró statisztikák előállnak:
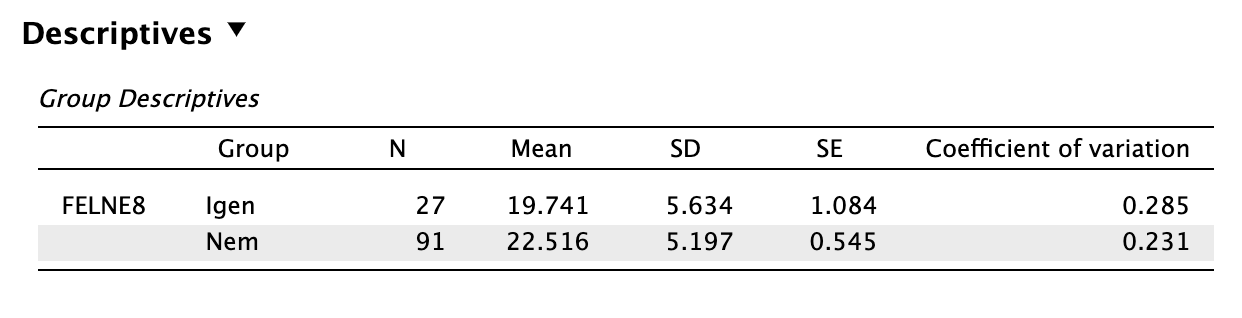
Megoldás 10.2. A depresszióval diagnosztizáltak és nem diagnosztizáltak FÉLNE-8 pontszámainak összehasonlítására kétoldalú függetlenmintás t-próbát végeztünk. Az adatok csoportonként normál eloszlást követtek (W(118) = 0,992, p = 0,719), számuk nem illesztett, de a szóráshomogenitás feltétele fennáll (Brown-Forsythe F(1, 116) = 0,434, p = 0,511), így a Student-féle t-próbát végeztük el. A depresszióval diagnosztizáltak FÉLNE-8 pontszáma (M = 19,74, SD = 5,63) statisztikailag szignifikánsan különbözik a depresszióval nem diagnosztizáltak pontszámától (M = 22,52, SD = 5,20), a különbség közepes hatásnagyságú: t(116) = -2,391, p = 0,018, d = -0,524.
Kiegészítés 10.1 (A Student-féle t-próba t-értékének kiszámítása). \[ t = \frac{\bar{x}_1-\bar{x}_2}{s_p \times \sqrt{\frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1 + n_2 - 2}}} \]
\[ s^2_p = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1 + n_2 - 2} \]
ahol: - \(\bar{x}_1\) és \(\bar{x}_2\) az 1. és 2. csoport mintaátlaga - n1 és n2 az 1. és 2. csoport mintaelemszáma - az s2p pedig a két csoport egyesített szórásnégyzete (mert azt feltételezzük, hogy a két csoport varianciája és ezáltal szórása egyenlő)
Kiegészítés 10.2 (A t-próba p-értékének kiszámítása). A kiszámított t-próba értékének a valószínűségét kiszámítjuk adott szabadságfokú (df) t-eloszláson.
Kétoldalú próba esetén
\[ p = 2 \times P(T > |t|) \]
Egyoldalú próba esetén \[ p = P(T > |t|) \]
VAGY
\[ p = P(T < |t|) \]
10.2 Függetlenmintás t-próbák: Welch-féle t-próba
A Welch-féle t-próba feltételei:
- A függő változó skála típusú
- A csoportok/minták függetlenek egymástól
- A függő változó megközelítőleg normál eloszlású csoportonként
A Welch-féle t-próbához nem szükséges feltétel a szóráshomogenitás. Így ezt a próbát alkalmazzuk, amikor a Levene- vagy Brown-Forsythe-próbánk szignifikáns (p < 0,05) eredményt ad.
Ehhez JASP-ban elegendő a függetlemintás t-próbák modulban kipiálni a Welch tesztet. (És saját magunk összezavarásának elkerülésére kivenni a pipát a Student teszt elől.)
Egy adatsor elemzése pontosan ugyanolyan elven történik, ahogy a Student-féle t-próba esetén láttuk, és az eredmények közlése is megegyezik (értelemszerűen a Student-féle próba helyett Welch-féle t-próbát hivatkozunk).
Kiegészítés 10.3 (A Welch-féle t-próba t-értékének kiszámítása). \[ t = \frac{\bar{x}_1-\bar{x}_2}{\sqrt{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}}} \]
ahol:
- \(\bar{x}_1\) és \(\bar{x}_2\) az 1. és 2. csoport mintaátlaga
- n1 és n2 az 1. és 2. csoport mintaelemszáma
- s1 és s2 az 1. és 2. csoport szórása
A próba szabadságfokát Welch–Satterthwaite-féle közelítéssel számítjuk.
\[ df \approx \frac{\left( \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} \right)^2}{\frac{\left( \frac{s_1^2}{n_1} \right)^2}{n_1 - 1} + \frac{\left( \frac{s_2^2}{n_2} \right)^2}{n_2 - 1}} \]
10.3 Függetlenmintás próba non-parametrikus változata: Mann-Whitney rangpróba
A Mann-Whitney-féle U próbát abban az esetben használjuk, ha az adataink nem követik a normál eloszlást vagy ordinális szintűek. Ebben az esetben teljesen mindegy, hogy a csoportok illesztettek-e és a szorásuk homogén-e. Azonban nagyon fontos, hogy a csoportok továbbra is függetlenek legyenek. A próba a két független minta mediánjának egyenlőségét teszteli.
A próbát hívhatjuk még függetlenmintás Wilcoxon rangösszeg próbának1.
A Mann-Whitney-féle rangpróba feltételei:
- A függő változó legalább ordinális mérési szintű
- A csoportok/minták függetlenek egymástól
A próbához kapcsolódó hipotézisek:
- Nullhipotézis (H0): A két csoport mediánja azonos. \(med(x-y)=0\)
- Alternatív hipotézis (H1): A két csoport mediánja eltér. \(med(x-y)≠0\)
A próba hatásnagyságát rang-biszeriális korrelációval számoljuk. Ehhez elegendő az Effect size Cohen’s d pontját kipipálnunk, a JASP a megfelelő mutatót automatikusan kiszámolja. Azonban itt nem a távolság-alapú Cohen-d értelmezést használjuk a hatás nagyságának eldöntésére, hanem a korrelációs együttható alapú megközelítést.
Példa 10.3 (Példa nem normál eloszlású adatok függetlenmintás próbájára) Szeretnénk megtudni, hogy az általunk mért félelem a negatív megítéléstől átlagpontszám (FÉLNE-8) különbözik-e a major depresszióval (F32.XX) diagnosztizáltak és nem diagnosztizáltak között.
Ezúttal az alábbi adatsort használjuk a személtetésre:
| BNO | N | Relatív gyakoriság |
|---|---|---|
| Igen | 68 | 50.0% |
| Nem | 68 | 50.0% |
A minta fő mutatói a FÉLNE-8 összpontszámokra vonatkozóan:
| Statistic | FELNE8 |
|---|---|
| N | 136.000 |
| Missing | 0.000 |
| Mean | 19.243 |
| SE (Mean) | 0.399 |
| SD | 4.656 |
| SE (SD) | 0.283 |
| Variance | 21.681 |
| SE (Var) | 2.639 |
| Median | 18.500 |
| Min | 5.000 |
| Max | 31.000 |
| IQR | 5.000 |
| Q1 (25%) | 17.000 |
| Q3 (75%) | 22.000 |
| Skewness | 0.176 |
| SE (Skew) | 0.208 |
| Kurtosis | 0.534 |
| SE (Kurt) | 0.413 |
| Shapiro W | 0.966 |
| Shapiro p | 0.002 |
Az adatsor itt letölthető: FELNE8_nonnormal.sav
Vizsgáljuk meg az előfeltételeket!
A függő változó legalább ordinális típusú?
Igen, Likert skálával mért itemek összpontszámáról van szó, így intervallumskálaként kezelhető változó.
A csoportok függetlenek egymástól?
Igen, nem lehet valaki egyszerre depresszióval diagnosztizált és nem diagnosztizált.
Állítsuk be a vizsgálatot JASP-ban!
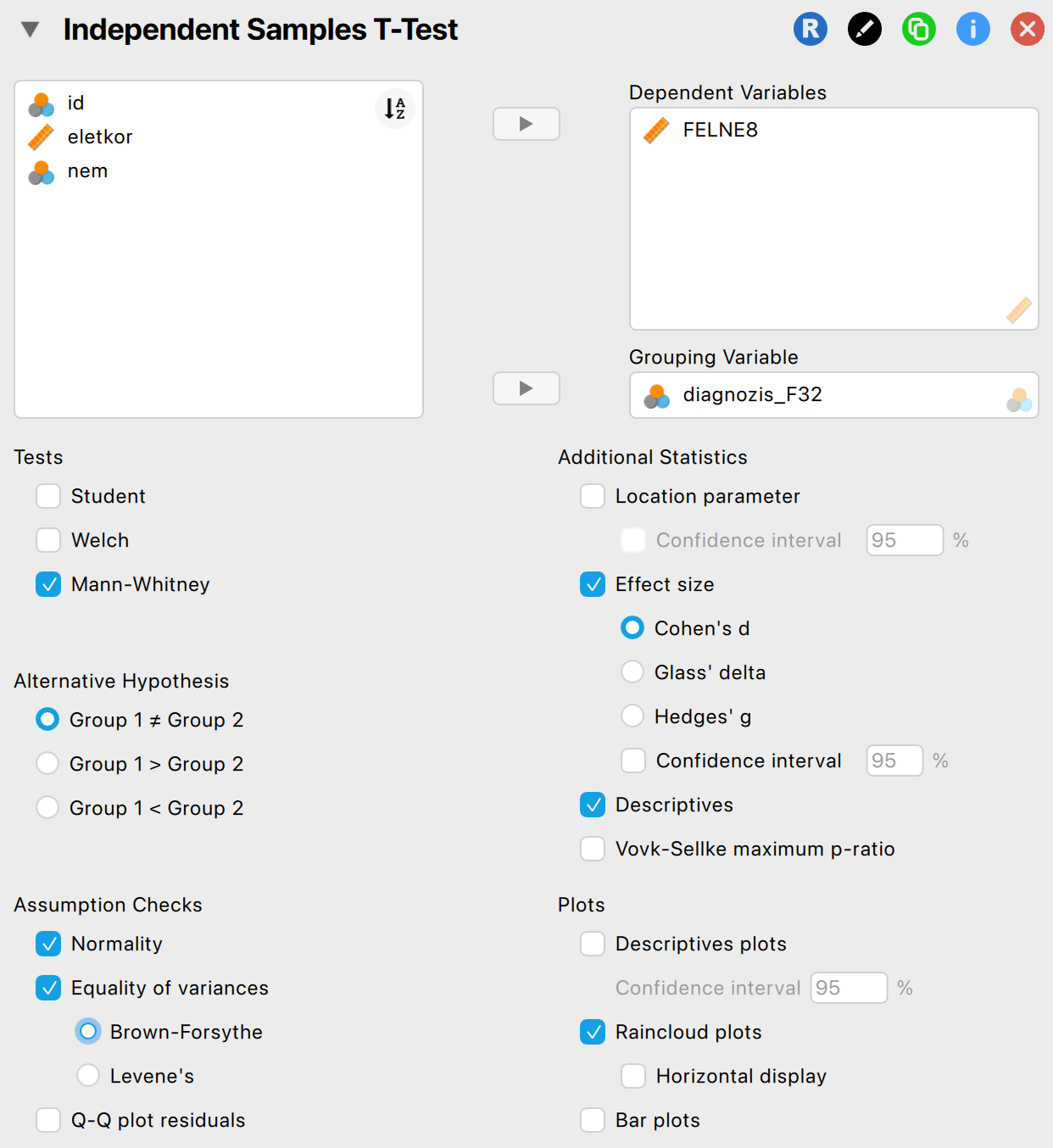
Olvassuk le és értelmezzük az eredményeket!
Normalitásvizsgálat eredménye

Láthatjuk, hogy a Shapiro-Wilk próba eredménye szignifikáns (p < 0,05), tehát a változó csoportonként nem követi a normál eloszlást, ezért parametrikus próbát nem végezhetünk.
Szóráshomogenitás-vizsgálat eredménye
Bár a Mann-Whitney rangpróbához nem szükséges feltétel, olvassuk le az eredményét.

A Brown-Forsythe-próba eredménye is szignifikáns (p < 0,05), tehát a csoportok varianciája és szórása közel sem azonos. (Ugyan illesztettek az elemszámok a csoportok között, de nem normál az eloszlásuk, ezért Levene próba nem végezhető így sem.)
A Mann-Whitney rangpróba eredménye.

A JASP a megjegyzések között jelzi nekünk, hogy a lehetséges t-próbák közül a Mann-Whitney-féle rangpróbát végezzük („Mann-Whitney U test”).
A próba W-statiszikája: 1058.
A p-érték: 4e-08, vagyis helyesen hivatkozva p < 0,001. A próba szignifikáns, mert \(p < 0,05\).
Rang-biszeriális hatásnagyság: -0,542. Ez Cohen (1988) alapján nagy hatásnagyság. Figyeljünk, hogy itt a korrelációs együttható értelmezési táblázatát nézzük!
Az összehasonlítandó csoportátlagokat és mögöttes eloszlásokat az alábbi ábra szemlélteti:
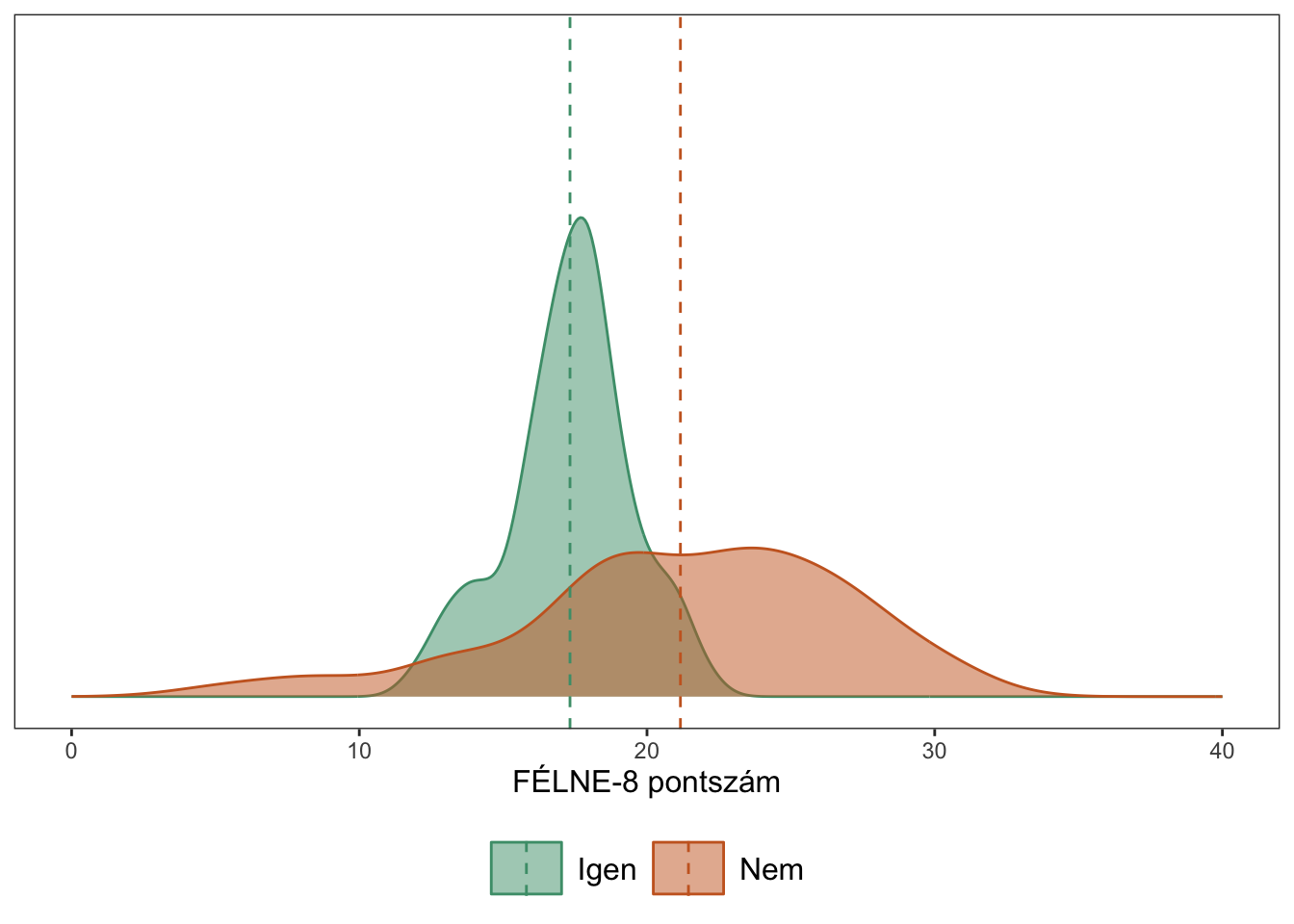
Egy boxplotpár és sűrűségfüggvény-pár kombinációját tartalmazó ábrát magunk is készíthetünk a JASP segítségével a modulon belül a Raincloud plots funkció kipipálásával. Az alapértelmezett ábra így fog kinézni:
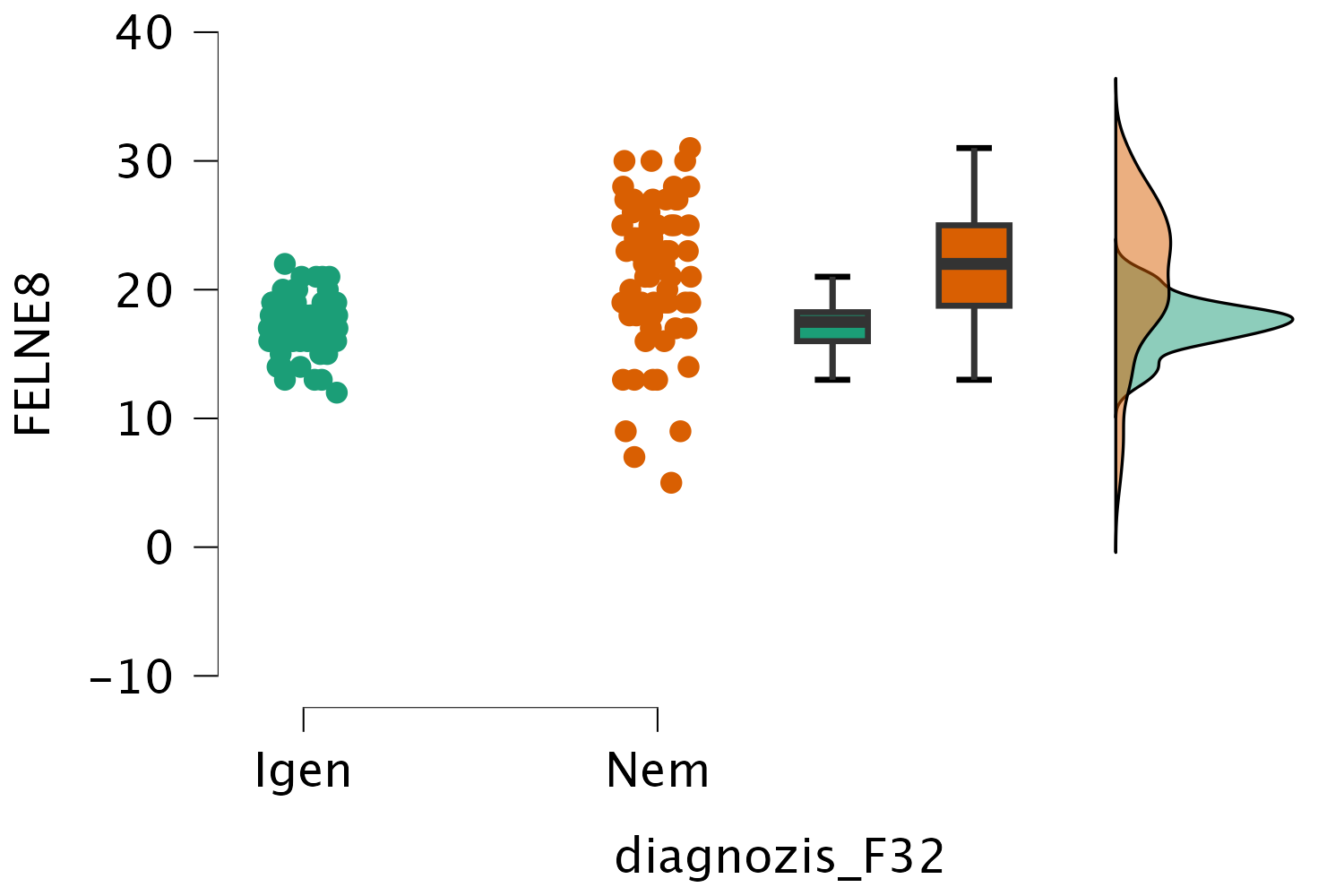
Ha szeretnénk, „horizontális” formát is válaszhatunk, ez esetben egymás alatt jelennek meg a sűrűségfüggvények, a boxplotok pedig vízszintesen:
A csoportok átlagát és szórását az eredmények közlésekor le kell írni. Ehhez nem szükséges elnavigálni, a t-próbáknál a Descriptives kipipálásával a szükséges leíró statisztikák előállnak:
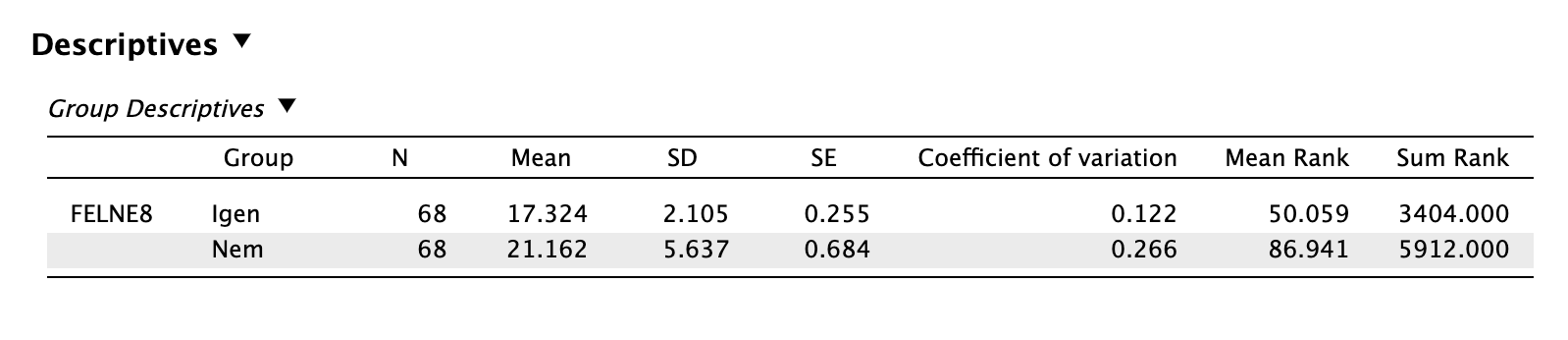
Megoldás 10.3. A depresszióval diagnosztizáltak és nem diagnosztizáltak FÉLNE-8 pontszámainak összehasonlítására kétoldalú függetlenmintás t-próbát végeztünk. Az adatok csoportonként nem követték a normál eloszlást (W(136) = 0,946, p < 0,001), számuk illesztett, és a szóráshomogenitás feltétele is sérül (Brown-Forsythe F(1, 134) = 37,222, p < 0,001), így Mann-Whitney-féle rangpróbát / függetlenmintás Wilcoxon rangösszeg próbát végeztünk, ami a t-próba nemparametrikus alternatívája.
A depresszióval diagnosztizáltak FÉLNE-8 pontszáma (M = 17,32, SD = 2,11) statisztikailag szignifikánsan különbözik a depresszióval nem diagnosztizáltak pontszámától (M = 21,16, SD = 5,64), a különbség nagy hatásnagyságú: W = 1058, p < 0,001, rrb = -0,542.
Nem összekeverendő a Wilcoxon előjeles rang próbával!↩︎