5  Korrelációs vizsgálatok

A korrelációs vizsgálatok során arra keressük a választ, hogy

• van-e valamilyen összefüggés, kapcsolat a vizsgálati változók között (együttjárás)
• milyen irányú a kapcsolat?
• mennyire szoros a kapcsolat?
• milyen hatással van az egyik változó változása a másik változóra?

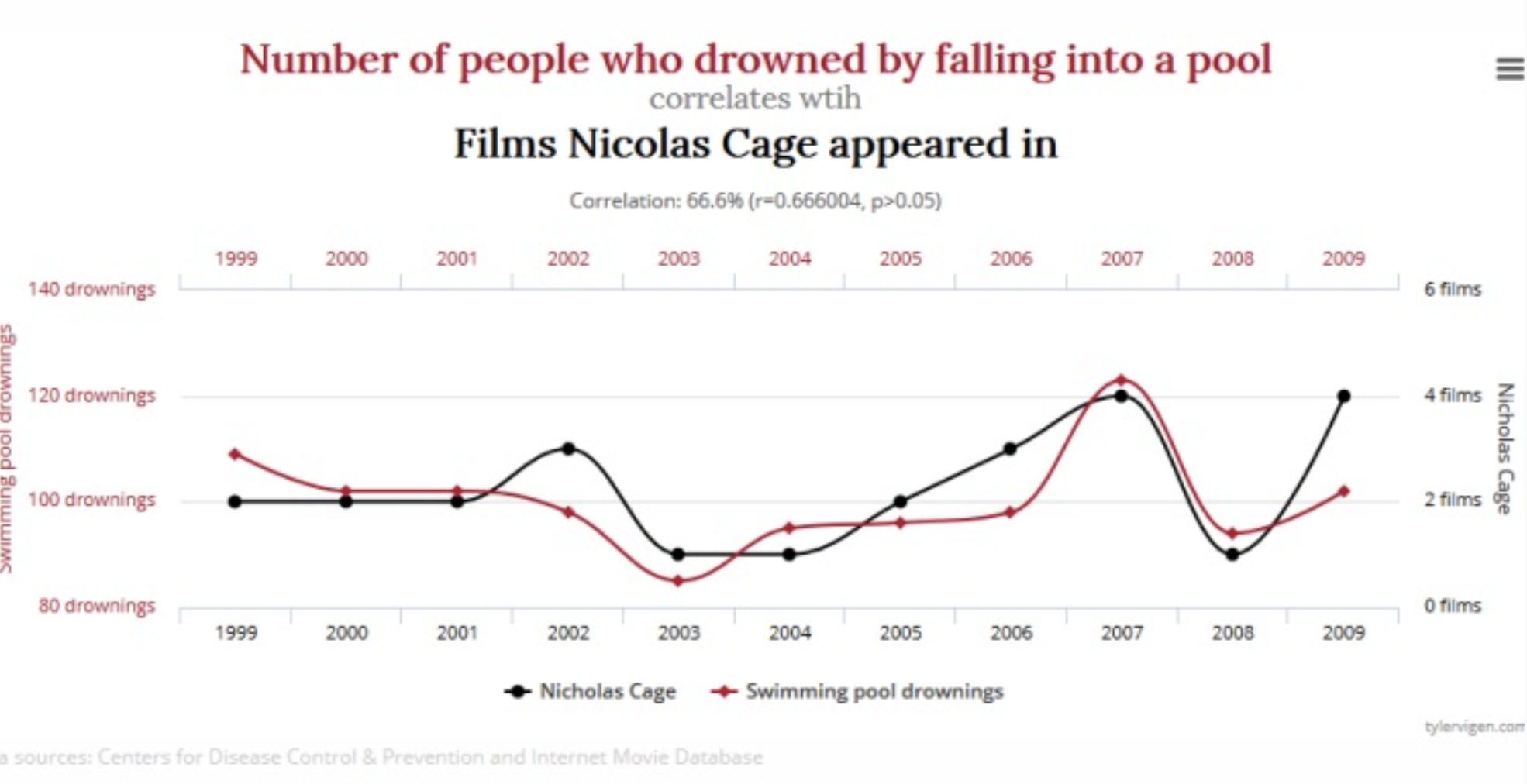
Az együttjárás viszont nem jelent ok-okozati kapcsolatot! Íme egy (ugyan nem szignifikáns, de közepes-erős) korreláció a Nicolas Cage filmdebut-k és medencébefúlás között:

A korrelációs vizsgálat során a két változót „felcserélhetjük” egymással, az eredményünk azonos marad. Később, a regressziós modelleknél keressük majd arra a választ, ha csak az egyik (független) változó predikálja a másik (függő vagy eredmény-)változót.

A korrelációs vizsgálatok megértéséhez szükségünk lesz újra az alábbi fogalmakra:

Variancia

annak a mértéke, hogy az egyes adatpontok milyen távolságban vannak az adatpontok átlagától, és így végső soron a többi adatponttól. A negatív és pozitív távolságok összeadáskor kioltanák egymást, ezért a különbségek négyzetre emelésével érjük el az előjel nélküli távolságokat, majd szabadságfokkal leosztva „átlagoljuk” őket.

A minta varianciája emlékeztetőül: \[ var(x) = s^2 = \frac{\sum_{i=1}^{n}{(X_i - \bar{X})^2}}{n-1} \]

Szórás

Hasonlóképpen azt jelzi, hogy a minta értékei mennyire szóródnak az átlag körül, de a gyökvonás miatt mértékegysége és skálája megegyezik az adatponttéval, így könnyebben értelmezhető.

A minta szórása emlékeztetőképpen \[ s = \sqrt{\frac{\sum_{i=1}^{n}{(X_i - \bar{X})^2}}{n-1}} \]

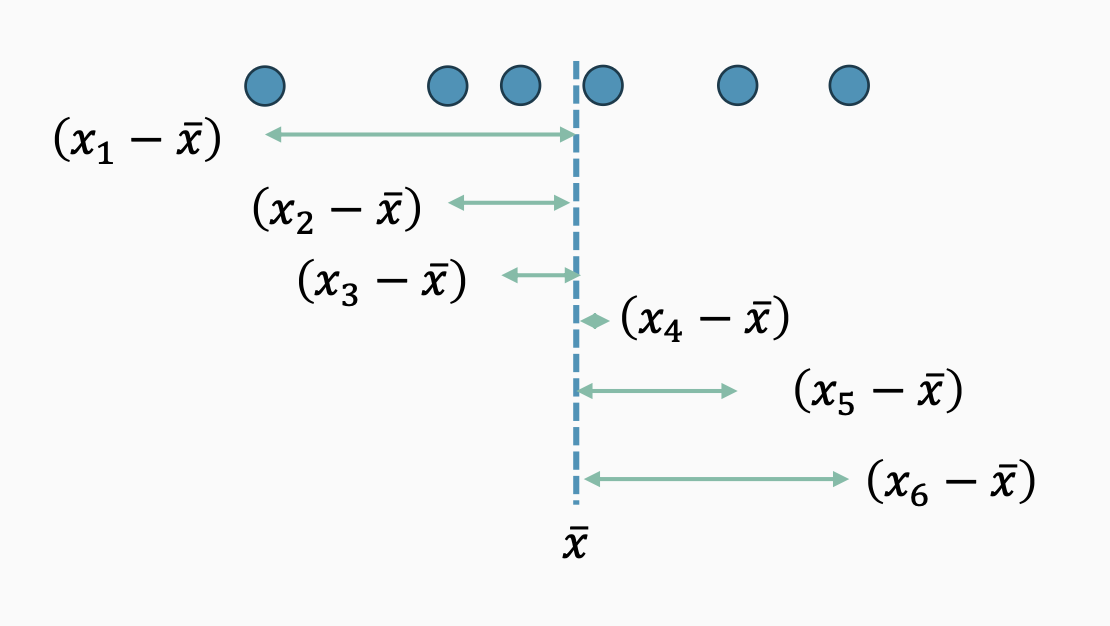
5.1 Kovariancia

Az első fontos új fogalom a kovariancia, ami azt mutatja, hogy merre mozognak az adatpontok egymáshoz képest.

A számítása során a két változó mozgását együttesen vesszük figyelembe a saját átlagukhoz képest (v.ö. variancia képlete):

\[ cov(x,y) = \frac{\sum_{i=1}^{n}{(x_i - \bar{x})(y_i - \bar{y})}}{n-1} \]

A kovariancia nulla, ha az eltérésszorzatok (\((x_i - \bar{x})(y_i - \bar{y})\)) összege kiegyenlíti egymást. Ha nem nulla, az előjele mutatja meg a kapcsolat irányát.

A kovariancia \(-\infty\) és \(+\infty\) között vehet fel értéket!

Mire jó a kovariancia?

• ebből számítjuk a korrelációs együtthatót
• tesztreliabilitás-számításhoz használjuk a pszichometriában
• főkomponens-elemzés alapja
• strukturális egyenletmodellezések elemzésének alapja
• lineáris regresszió együtthatója

A vizsgált változóink együttmozgását első lépésben tudjuk variancia-kovariancia mátrixon ábrázolni:

	x	y	z
x	var(x)	cov(x,y)	cov(x,z)
y	cov(x,y)	var(y)	cov (y,z)
z	cov(x,z)	cov(y,z)	var(z)

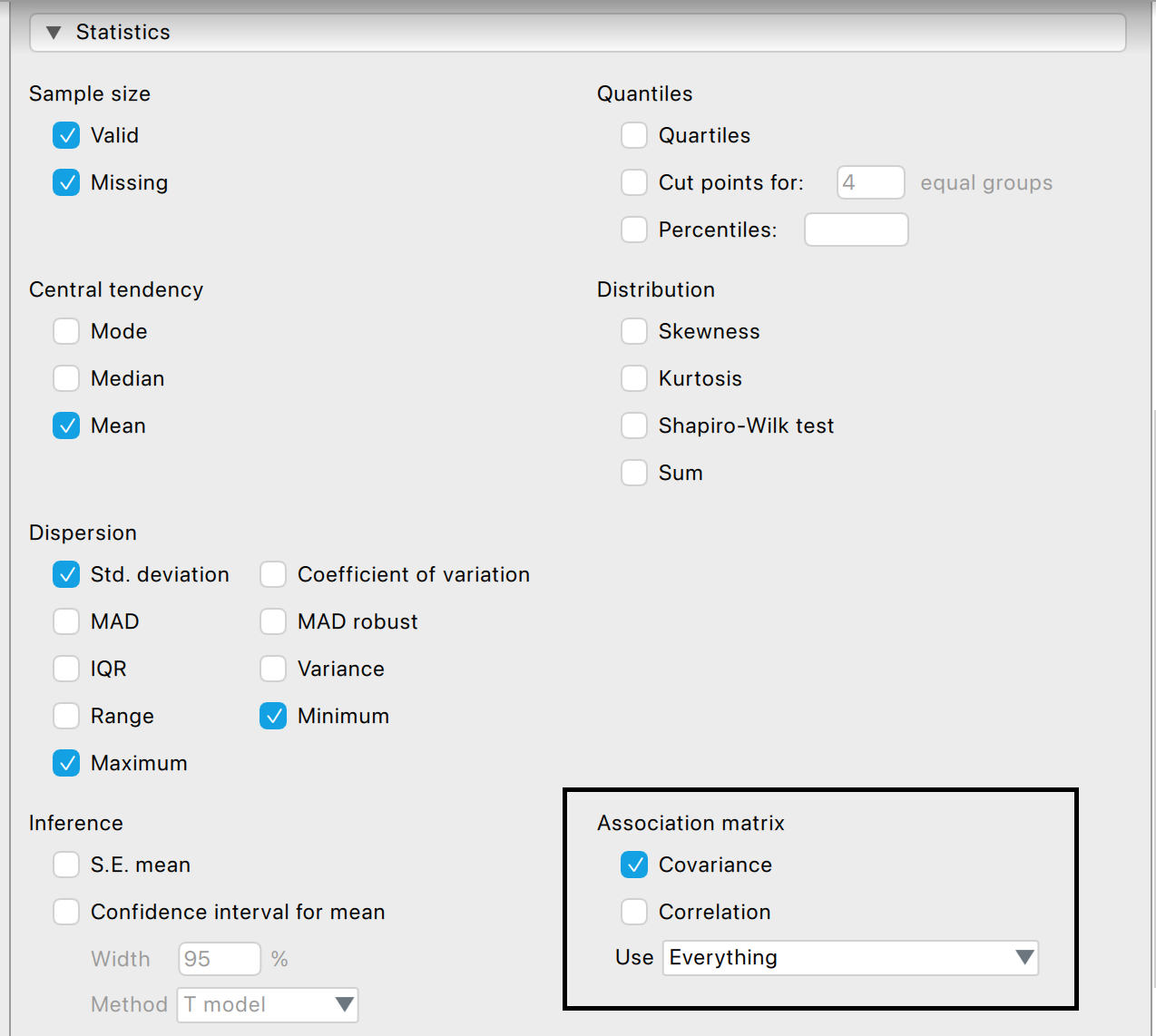
A kovarianciamátrixot a JASP leíró statisztika moduljában létre tudjuk hozni:

Példa 5.1 Megvizsgáljuk, hogy van-e kapcsolat az életkor és a Rövidített Beck Depresszió Kérdőív összpontszáma között a mintánkban (n = 7).

Adataink:

Életkor	Depresszió pontszám
20	6
42	11
35	8
46	15
57	10
71	9
35	7

Számoljuk ki az átlagokat:

\[ \begin{aligned} M_{é} &= \frac{\sum_{i=1}^{n}{X_i}}{n} = \\ &= \frac{20+42+35+46+57+71+35}{7} = \\ &= 43{,}714 \end{aligned} \]

\[ \begin{aligned} M_{BDI} &= \frac{\sum_{i=1}^{n}{X_i}}{n} = \\ &= \frac{6+11+8+15+10+9+7}{7} = \\ &= 9{,}429 \end{aligned} \]

És a varianciákat:

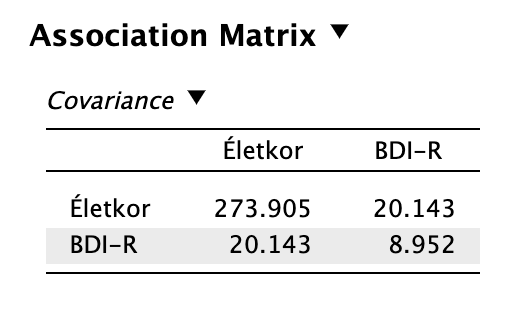
\[ \begin{aligned} var({életkor}) &= \frac{\sum_{i=1}^{n}{(X_i - \bar{X})^2}}{n-1} = \\ &= \frac{(20-43{,}714)^2 + (42-43{,}714)^2 + ...}{7-1} = \\ &= 273{,}905 \end{aligned} \]

\[ \begin{aligned} var({BDI}) &= \frac{\sum_{i=1}^{n}{(X_i - \bar{X})^2}}{n-1} = \\ &= \frac{(6-9{,}429)^2 + (11-9{,}429)^2 + ...}{7-1} = \\ &= 8{,}952 \end{aligned} \]

Természetesen ezeket a JASP leíró statisztikai moduljában le tudjuk olvasni mindenféle számolgatás nélkül. De a levezetés lényege, hogy lássuk, hogy mik a közös elemek a képletekben és ezek hogyan függnek össze.

\[ \begin{aligned} cov(x,y) &= \frac{\sum_{i=1}^{n}{(x_i - \bar{x})(y_i - \bar{y})}}{n-1} = \\ &= \frac{(20-43{,}714) \times (6-9{,}429) + (42-43{,}714) \times (11-9{,}429) + ...}{7-1} = \\ & = \frac{120{,}8571}{6}=20{,}143 \end{aligned} \]

Ezzel megkapjuk a választ arra, hogy van-e kapcsolat és annak milyen az iránya.

Megoldás 5.1.

	életkor	BDI-R pontszám
életkor	273,905	20,143
BDI-R	20,143	8,952

Az életkor és a depresszió pontszámok között pozitív irányú kapcsolatot találtunk (cov(életkor,BDI-R) = 20,143 > 0).

5.2 Korrelációs együttható

A kovarianciával több problémánk van. Nem tudja megadni a kapcsolat erősségét, legalábbis nem összehasonlítható módon. Mértékegysége nehezen vagy egyáltalán nem értelmezhető. Értéke bármilyen értéket felvehet, aminek értelmezéséhez nehéz útmutatót készíteni.

Ezekre a problémákra ad választ a korrelációs együttható, ami az együttjárás szorosságának a mérőszáma.

Többféle korrelációs együtthatót ismerünk és használunk:

• Pearson-féle korrelációs együttható (\(r\) vagy \(r_p\)): a lineáris kapcsolat korrelációs együtthatója normál eloszlású skálaváltozók esetén
• Spearman-féle (rang)korrelációs együttható (\(r_s\) vagy \(\rho\) (rhó)): normál és nemnormál eloszlású skála típusú változó vagy ordinális változó esetén is használhatjuk; a kapcsolat nem kell lineáris legyen, de monotonnak kell lennie. Nemparametrikus mutató
• Kendall-tau (\(\tau\) vagy \(r_\tau\)): ordinális változó vagy kis elemszámú minta esetén használjuk. Ugyanúgy monoton kapcsolatot feltételez, mint a Spearman-féle korrelációs együttható. Nemparametrikus mutató.
• Cramér-féle V (): a nominális változók közötti együttjárás erősségét mérő mutató. A \(\chi^2\) próbák során használjuk hatásnagyságként.
• rang-biszeriális korreláció (\(r_{rb}\)): dichotóm nominális változó és ordinális változó közötti kapcsolat kimutatására szolgál. Hatásnagyságmutatóként is alkalmazzuk a t-próbákat helyettesítő egyes nemparametrikus próbáknál.
• pont-biszeriális korreláció (\(r_{pb}\)): dichotóm nominális változó és skála típusú változó közötti kapcsolat mérésére szolgál

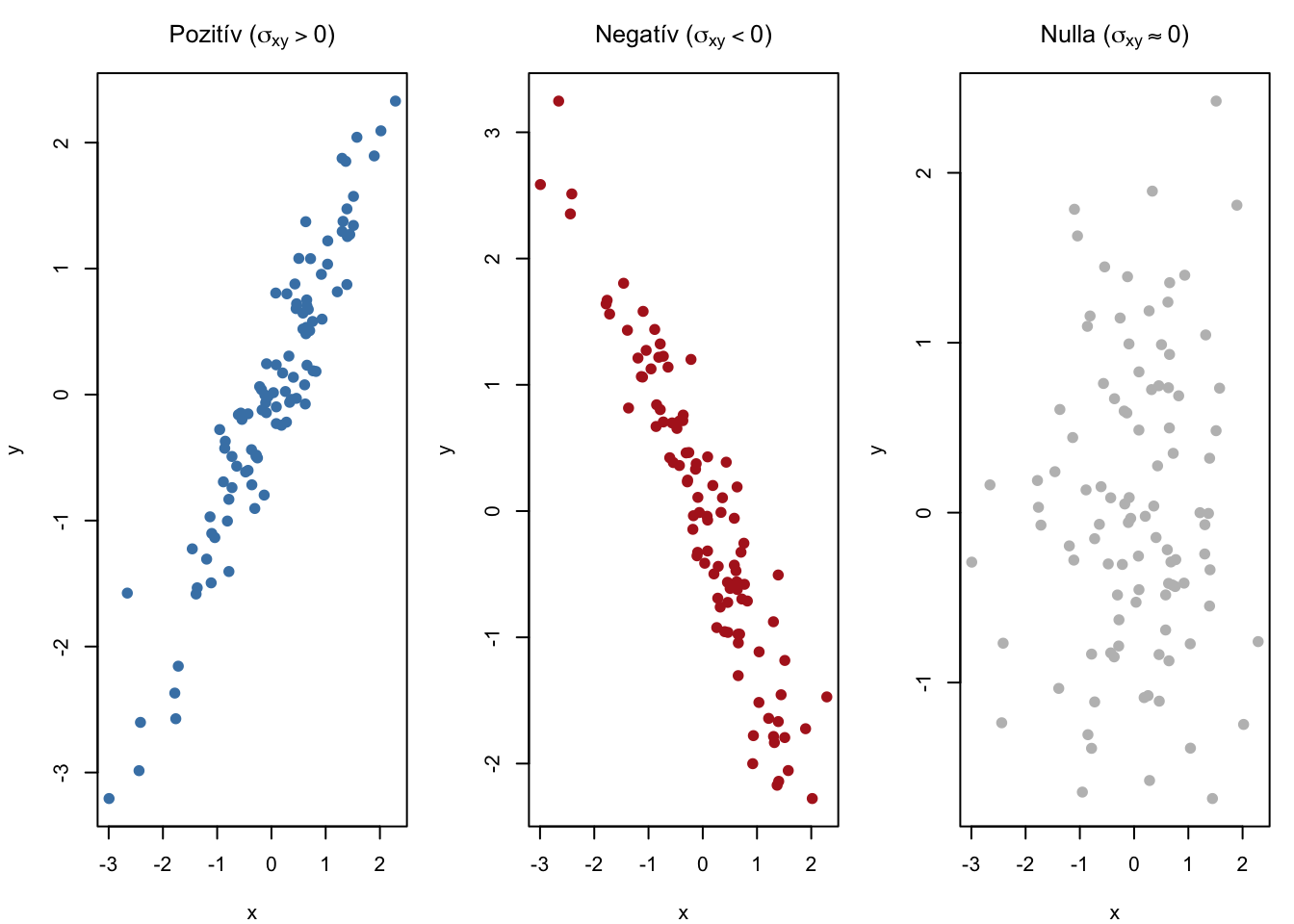
A korrelációs együttható -1 és 1 közötti értéket vehet fel. Előjele a korreláció irányát mutatja.

• A változók tökéletes függetlenségét jelenti, ha r = 0.
• Pozitív kapcsolat (r > 0): ha egyik változó nő, a másik is nő
• Negatív kapcsolat (r < 0): ha egyik változó nő, a másik csökken
• Tökeletes függvényszerű kapcsolatot jelez, ha r = -1 vagy r = 1.

Erősségét többféle módon értelmezi a szakirodalom. Ezek közül fontos lehet:

• Cohen (1988) ajánlása a legelterjedtebb értelmezés.
• Evans (1996) ajánlása szigorúbb, a klinikai/orvosi mérésekhez használt.
• Hemphill (2003) túl szigorúnak véli a Cohen-féle sávokat, szerinte ezek nem teljesíthetők a pszichológiai kutatásokban¹, meta-analízisek alapján állított fel sávokat.
• Gignac & Szodorai (2016) szintén túl szigorúnak találta Cohent, és szintén metaanalízis alapján állított össze egy sokkal megengedőbb értelmezési keretet.
• Funder & Ozer (2019) szintén enyhébb értelmezést dolgozott ki.
• Lovakov & Agadullina (2021) szintén egy sajátos értelmezést dolgozott ki.

Forrás	Gyenge/kicsi	Közepes	Erős/nagy	Nagyon nagy
Cohen (1988)	0,10-0,29	0,30-0,49	0,50	-
Evans (1996)	0,20-0,39	0,40-0,59	0,60-0,79	> 0,80
Hemphill (2003)	< 0,20	0,20-0,30	> 0,30	-
Gignac & Szodorai (2016)	0,10	0,20	0,30	-
Funder & Ozer (2019)	0,10	0,20	0,30	> 0,40
Lovakov & Agadullina (2021)	0,12	0,24	0,41	-

A korrelációs együttható értelmezése úgy teljes, ha vizuálisan is szemléljük az adatokat egy ábrán, ahol a korrelációs együttható meredeksége is szerepel. Tekintsük meg az ábrát úgy, hogy kitakarjuk az ábra bal és jobb oldalát, majd megnézzük, hogy pontfelhő valamilyen kapcsolatra hasonlító alakot vesz-e föl, vagy a zéró korrelációhoz/kovarianciához hasonlóan diffúz.

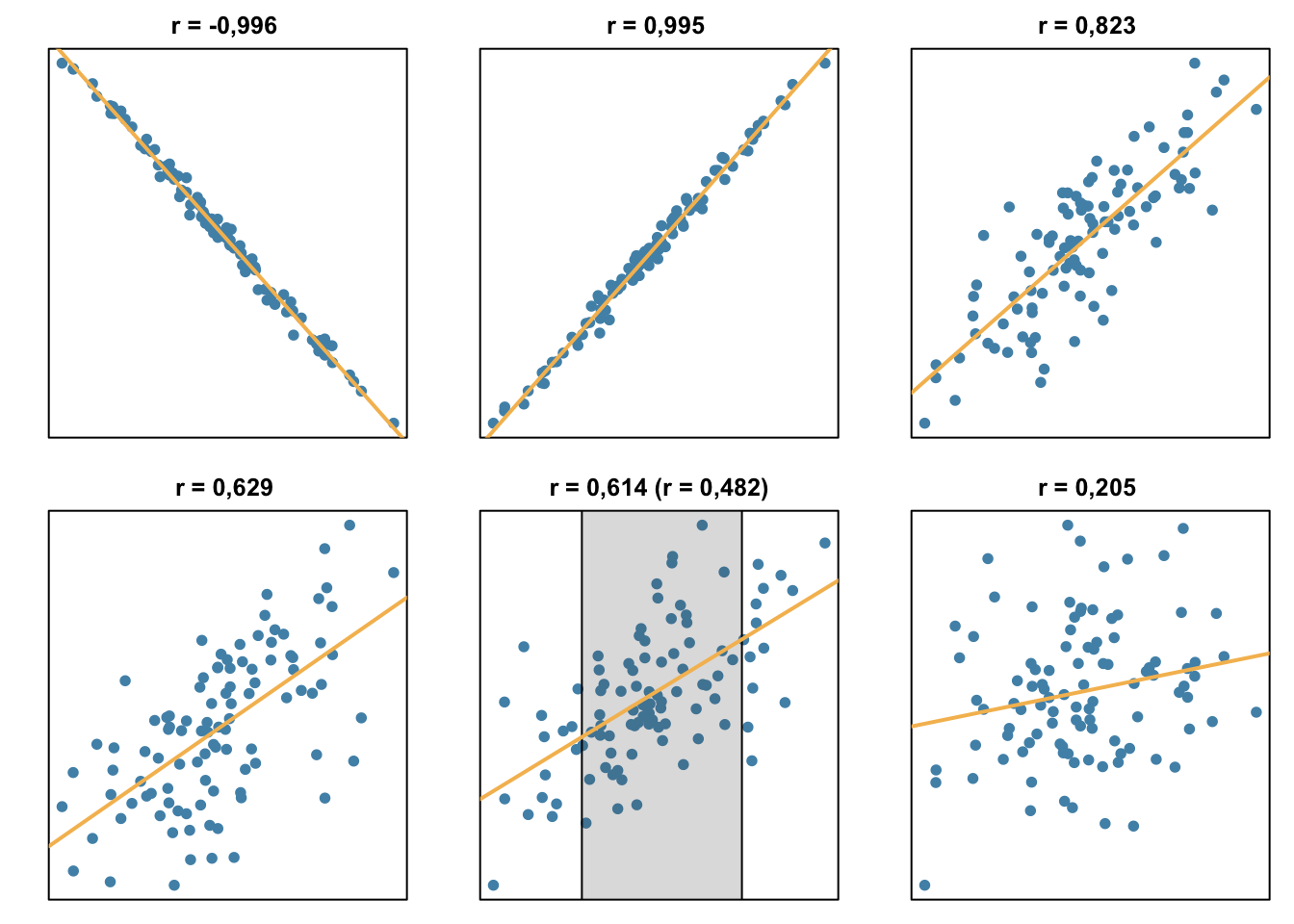
Láthatjuk, hogy a szürkével jelölt ponthalmaz korrelációs együtthatója alacsonyabb, mint a teljes ponthalmazé.

Azt is észrevehetjük, hogy minél közelebb helyezkedek el a pontok az egyeneshez, annál erősebb korrelációról beszélhetünk.

5.2.1 Pearson-féle korrelációs együttható

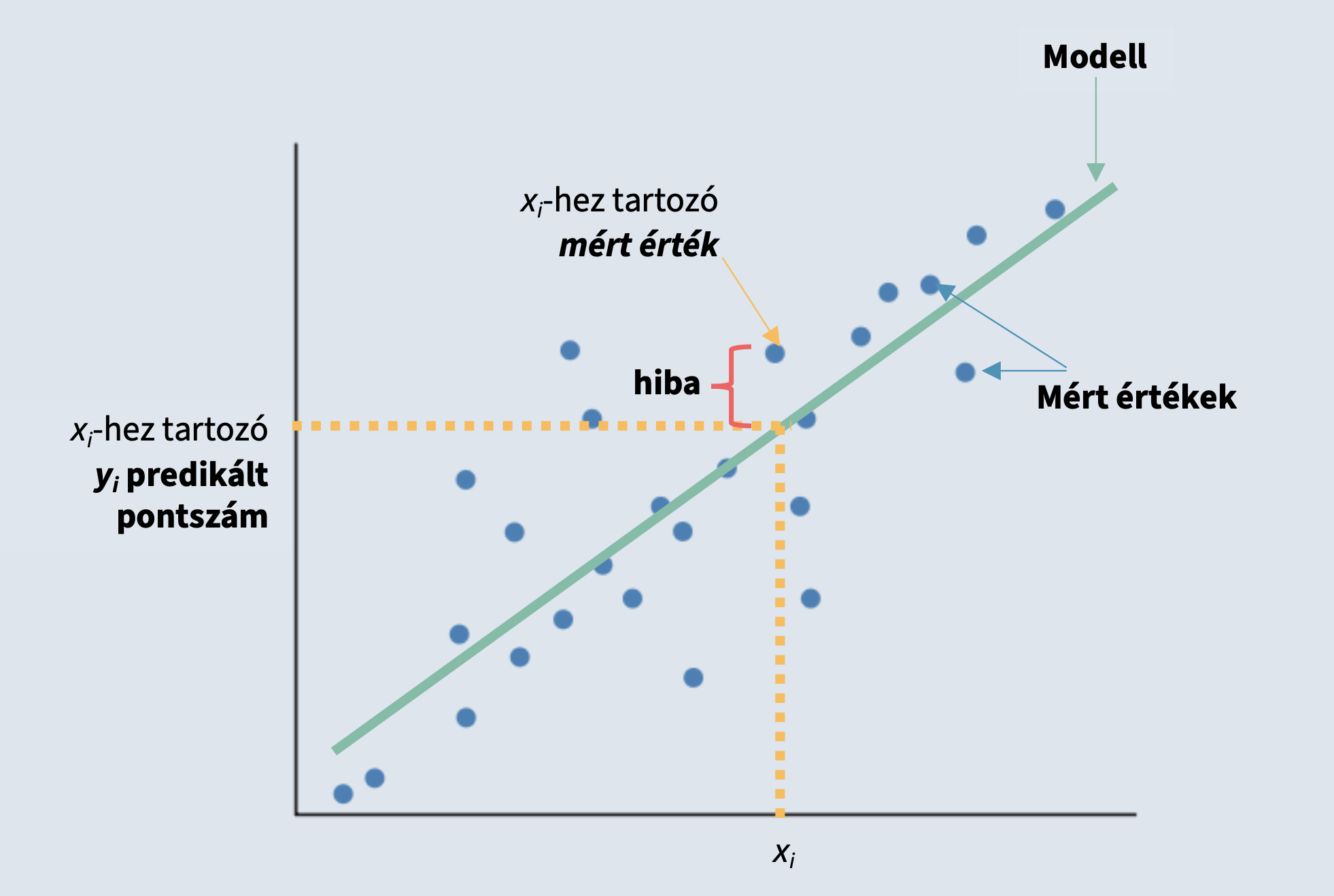
Az ábrán a pontok jelölik a mért értékeket (ti. a tényleges x és y változónk valós elhelyezkedése az ábrán), a zöld egyenes jelöli a korrelációs együttható meredekségével rendelkező egyenest. Az egyenesen lévő értékek a predikált értékek. Míg a tényleges értékek és a predikált értékek közötti távolság a hiba.

A Pearson-féle korrelációs együttható feltételei:

• mindkét vizsgált változó skála típusú
• a vizsgált változók normál eloszlásúak (többdimenzionális és páronkénti normalitást ellenőrizve)
• az adatokban nincsenek erősen torzító kiugró értékek
• a változók közötti kapcsolat monoton és lineáris

\[ r = \frac{cov(x,y)}{s_x \times s_y} \]

A normalitásvizsgálat protokollja skálaváltozók esetére:

• 2-nél több változó korrelációs analízise esetén a többdimenziós normalitást vizsgáljuk multidimenzionális Shapiro-Wilk-próbával a JASP-ban. Amennyiben ennek eredménye szignifikáns (\(p < 0{,}05\)), úgy Pearson-korreláció nem végezhető, hanem csupán Spearman-féle korrelációs vizsgálat. Ha nem szignifikáns (\(p > 0{,}05\)), akkor még nem fogadjuk el automatikusan a normalitást, hanem…

• megvizsgáljuk a páronkénti normalitást. Ha a páronkénti kétdimenzionális normalitásvizsgálaton (szintén multidimenzionális Shapiro-Wilk-próbát alkalmaz a JASP, de csak a párokból képez vizsgálati alapot) bármelyik páros próbája szignifikáns (\(p < 0{,}05\)), akkor is Spearman-féle korrelációs vizsgálatot kell alkalmaznunk. Tehát ez az erősebb feltétel.

Példa 5.2 Megvizsgáljuk, hogy van-e kapcsolat az életkor és a Rövidített Beck Depresszió Kérdőív összpontszáma között a mintánkban (n = 76).

Az adatsor itt letölthető: Eletkor_BDI.sav

1. Állítsuk be a vizsgálatot JASP-ban!

2. Olvassuk le az eredményeket!

   1. Először a normalitásvizsgálatot végezzük el!

      

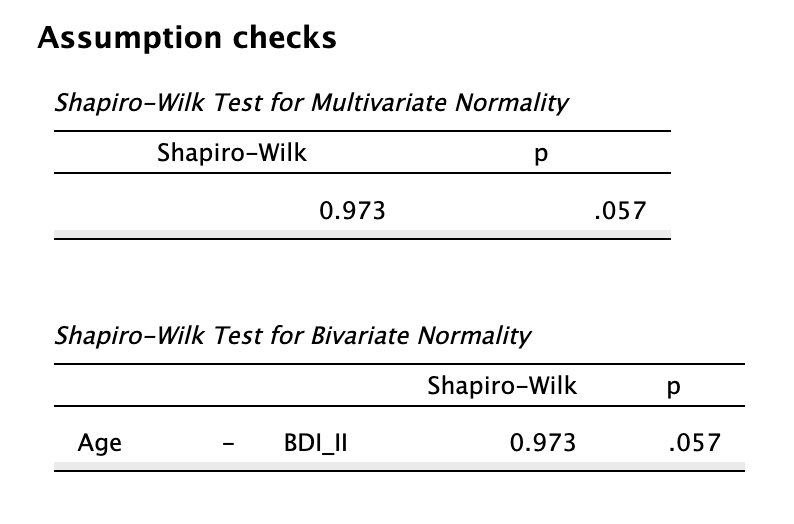
      Példánkban csak két változót vizsgálunk, tehát a páronkénti (kétdimenziós) normalitásvizsgálat és a többdimenziós normalitás eredménye egybeesik. Az eredmény nem szignifikáns, mert \(p = 0{,}057 > 0{,}05\).

      Tehát nem szükséges semmit átállítanunk, leolvashatjuk a Pearson-féle vizsgálat eredményét.

   2. A korrelációs együttható leolvasása

      

      • r korrelációs együttható: 0,305. Ez azt jelenti, hogy a változók között pozitív irányú a kapcsolat, mert r > 0. Nagyságát tekintve közepesnek tekinthető (de attól függ, melyik értelmezési keretet alkalmazzuk).

      • A próba szignifikanciája: p = 0,007. Mivel p < 0,05, ezért a próbát szignifikánsnak tekinthetjük.

Megoldás 5.2. Az életkor és depresszió pontszámok közötti együttjárás megállapítására korrelációs vizsgálatot végeztünk. Az adatok páronként normál eloszlást követnek (W(76) = 0,973, p = 0,057), ezért Pearson-féle korrelációs együtthatót számítottuk ki. A próba statisztikailag szignifikáns és közepes mértékű együttjárást mutat az életkor és a BDI-vel mért depresszió konstruktuma között: r = 0,305, p = 0,007.

5.2.2 Spearman-féle korrelációs együttható

A Spearman-féle együttható pontosan ugyanolyan valid² és hasonlóképp kell értelmezni, mint a Pearson-féle együtthatót.

A Spearman-féle korreláció alkalmazható, ha legalább az egyik feltétel fennáll:

• A vizsgált változók ordinális vagy skála típusú változók
• A vizsgált változók nem kell normál eloszlásúak legyenek
• Az adatokban lehetnek kiugró értékek
• A változók közötti kapcsolat nem kell lineáris legyen, de legalább monoton kell legyen.

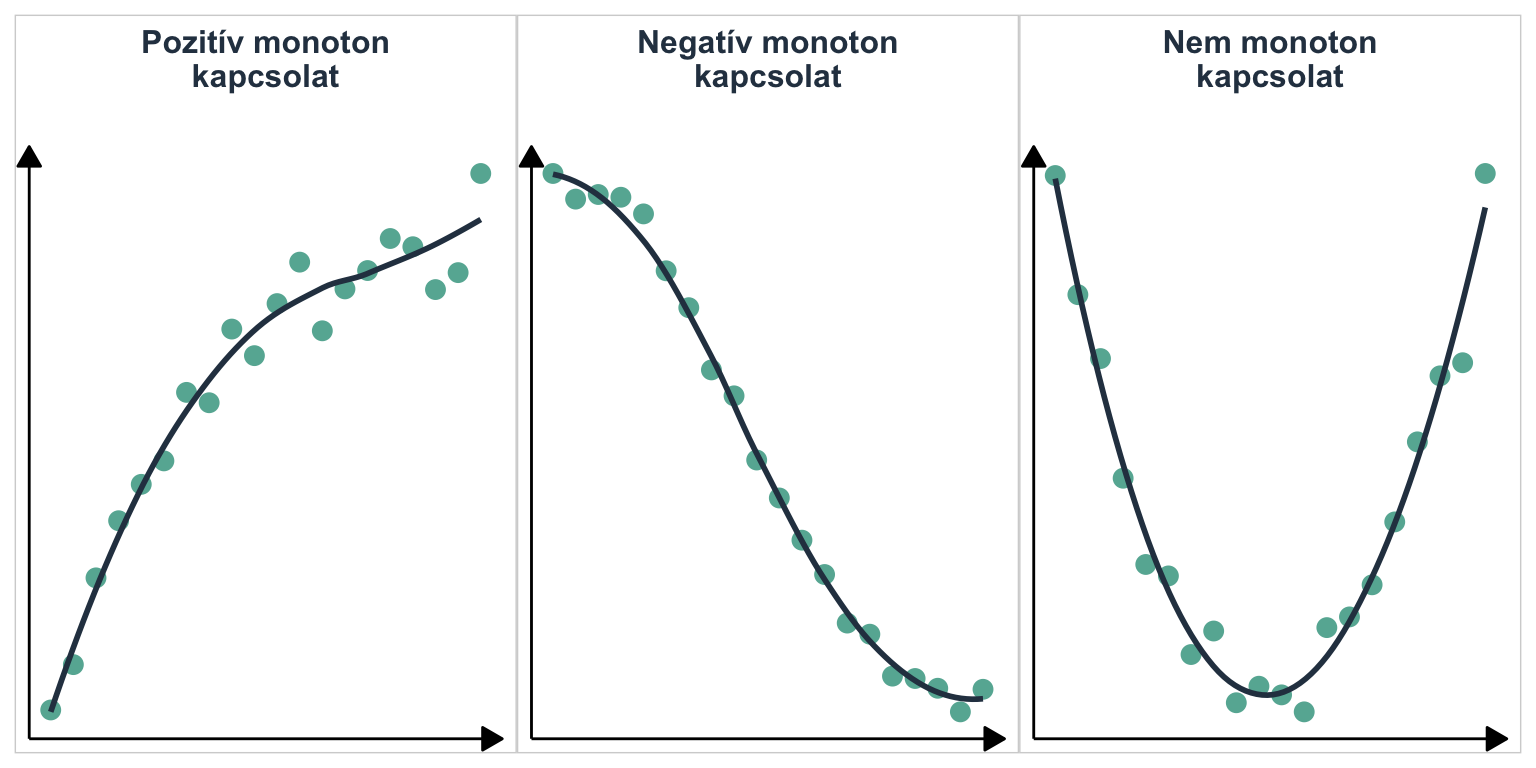
A Spearman-féle korrelációs együttható képlete: \[ r_s = 1 - \frac{6\sum_{i=1}^n{d_i^2}}{(n^3-n)} \]

ahol d a rangpárok közötti különbség

Ismétlődő rangok esetén: \[ r_s = 1 - \frac{6[\sum_{i=1}^n{d_i^2}+\frac{\sum{(m^3-m)}}{12}]}{(n^3-n)} \]

ahol m a rangismétlések száma ismétlődő rangonként.

JASP-ban az egyetlen változtatás, hogy a Spearman’s rho próbát kell bepipálni (és a félreértések elkerülése végett a Pearson’s r-ből kivenni a pipát).

5.2.3 Kendall-tau

A Kendall-tau együtthatót akkor számítjuk ki, amikor legalább az egyik feltétel fennáll:

– A vizsgált változók ordinális változók – A vizsgált változók nem kell normál eloszlásúak legyenek – Az adatokban lehetnek kiugró értékek – A változók közötti kapcsolat nem lineáris, de legalább monoton

Kis elemszám esetén ez preferált a Spearman-féle rhóval szemben.

\[ \tau = \frac{n_c - n_d}{\frac{n(n-1)}{2}} \]

ahol n_c a konkordáns párok száma, n_d a diszkordáns párok száma.

A Kendall-féle tau együttható alapja a konkordáns és diszkordáns párok különbsége. Ennek megértésére használjuk az alábbi ábrát!

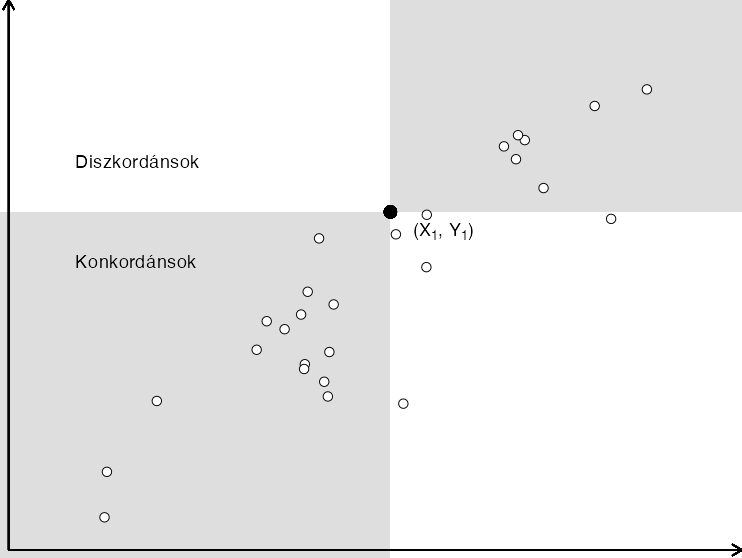
A fekete adatpont (x₁, y₁) konkordáns párjai a szürke háttérrel jelölt zónában lehetnek. Konkordáns pár az, ami az x₁ és y₁ koordináta mindkét eleménél nagyobb vagy mindkét eleménél kisebb.

Tehát formálisan konkordáns két pár, ha:

\[ \begin{cases} x_i < x_j \text{ és } y_i < y_j \\ \text{vagy} \\ x_i > x_j \text{ és } y_i > y_j \end{cases} \]

Diszkordáns minden olyan pár, ami az x₁ és y₁ koordináta egyik eleméhez képest nagyobb, míg másik eleméhez képest kisebb.

\[ \begin{cases} x_i > x_j \text{ és } y_i < y_j \\ \text{vagy} \\ x_i < x_j \text{ és } y_i > y_j \end{cases} \]

A Kedall-tau érték kiszámítását ugyanazon a panelen kérhetjük a JASP-tól, ahol a Pearson vagy Spearman korrelációs együtthatókat kértük.

5.3 Determinációs együttható

A determinációs együttható egy hatásnagyság-mutató. Megmutatja, hogy a független változók mekkora hányadban (százalékban) magyarázzák meg a függő változó szóródását vagy varianciáját. Más szóval az y variabilitásának azon része, amit a regressziós egyenes megmagyaráz.

Jele: \(r^2\)

Kiszámítása: a Pearson-féle korrelációs együttható négyzetre emelése

5.4 Kvalitatív változók vizsgálata

5.4.1 Cramér-féle V (kontingencia-együttható)

Nominális adatok esetén használjuk. Alapja a \(\chi^2\) érték, de a Cramér-féle V sztenderdizált, nem függ a mértékegységtől: 0 és 1 közötti értéket vehet fel.

\[ V = \sqrt{\frac{\chi^2}{n(k-1)}} \]

Példa 5.3 Vizsgáljuk meg, hogy van-e kapcsolat az alkalmazott terápiás módozatok (CBT, sématerápia, pszichodinamikus terápia) és aközött, hogy milyen pszichiátriai diagnózissal érkezett a páciens (borderline, kevert szorongásos zavar). Mintánkban n = 25 fő szerepel.

Az adatsor itt letölthető: terapia_diagnozis.sav

Nominális változókról lévén szó, kontingenciatáblát készítünk a JASP-ban.

Állítsuk be a vizsgálat elemeit JASP-ban:

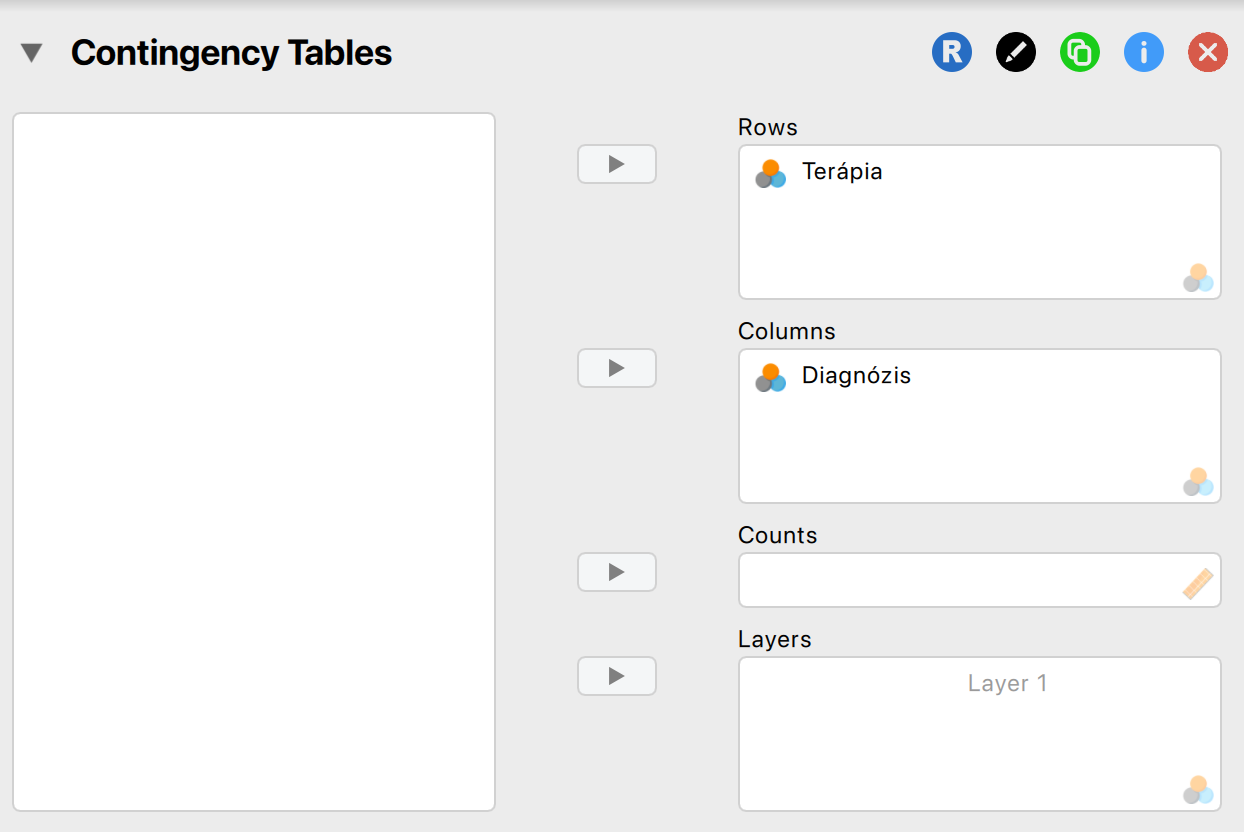
Olvassuk le az eredményeket!

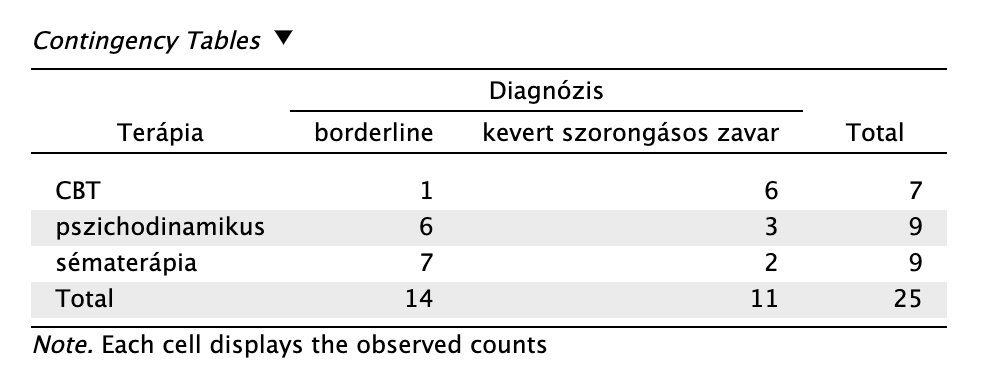
Láthatjuk, hogy a kevert szorongásos zavarral érkező páciensek főleg kognitív viselkedésterápiában, míg a borderline diagnózissal érkezők közel fele-fele arányban sématerápiában vagy pszichodinamikus terápiában részesültek.

A kapcsolat vizsgálatára khí-négyzet próbát végeztünk JASP-ban, melynek eredménye:

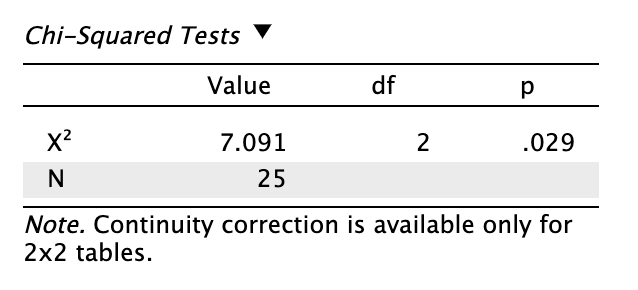
Láthatjuk, hogy az eredmény szignifikáns (p < 0,05), mert p = 0,029. Tehát van kapcsolat a terápiás módozat és diagnóznis között.

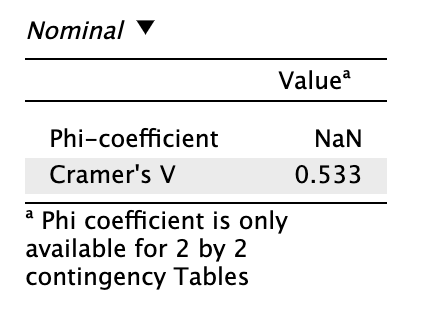
A kapcsolat nagyságát a Cramér-féle V kontingencia-együttható mutatja meg: 0,533.

Megjegyzés: kis elemszám miatt a Yates-korrekcióról és a Fisher-exact próbáról szót kellene ejtenünk, de itt a cél a khí-négyzet próba szemléltetése volt.

Megoldás 5.3. A terápiás módszer (CBT, pszichodinamikus, sématerápia) és a pszichiátriai diagnózis (borderline, kevert szorongásos zavar) közötti összefüggést Pearson-féle khí-négyzet próbával vizsgáltuk. Az elemzés statisztikailag szignifikáns kapcsolatot mutatott a két változó között: χ²(2,N=25)=7,091, p = 0,029. A kapcsolat erőssége a Cramer-féle V együttható alapján nagynak tekinthető (V = 0,533).

5.4.2 Pont-biszeriális kapcsolat

Egy dichotóm (csak két értéket felvevő) és egy skála típusú változó közötti kapcsolat erősségét mutatja meg.

\[ r_{pb} = \frac{\bar{X}_1 - \bar{X}_0}{s_n} \times \sqrt{\frac{n_1 \times n_2}{n^2}} \]

A JASP-ban elég megtévesztő módon ugyanúgy a korrelációs modulban érthető el, és a dichotóm változót (hiába van nominálisként kódolva) ugyanúgy a változók közé kell behúzni. A JASP pszeudo-skálává alakítja (kis csillag jelenik meg a vonalzó ikon mellett). A Pearson-féle együtthatót kell kipipálni továbbra is, de ne tévesszen meg minket, valójában a pont-biszeriális együtthatót számolja ki a szoftver. YouTube útmutató

Érdekesség még, hogy a pont-biszeriális kapcsolatvizsgálat során kapott p-érték megegyezik a függetlenmintás t-próba p-értékével.

A pont-biszeriális korreláció feltétele, hogy a skála típusú változó normál eloszlást kövessen, vagy az, hogy a skála változó szórása dichotóm csoportonként homogén legyen. JASP-ban a normalitás feltételét tudjuk vizsgálni a korrelációs modulban.

Példa 5.4 Kutatásunkban szerettük volna megvizsgálni, hogy van-e összefüggés a szuicid kísérletek (1: megkísérelt öngyilkosságot, 0: nem kísérelt meg öngyilkosságot) és a Beck-féle reménytelenség skála pontszáma között (N = 28). Klinikai kutatásokból tudjuk, hogy a 9 pontszám fölött erős a szuicid veszélyeztetettség (Perczel Forintos Dóra, 2018).

Az adatsor itt letölthető: remenytelenseg.sav

Állítsuk be a pont-biszeriális korrelációt a JASP-ban! (Ne feledjük, hogy úgy kell beállítsuk, mintha Pearson-korrelációt vizsgálnánk.)

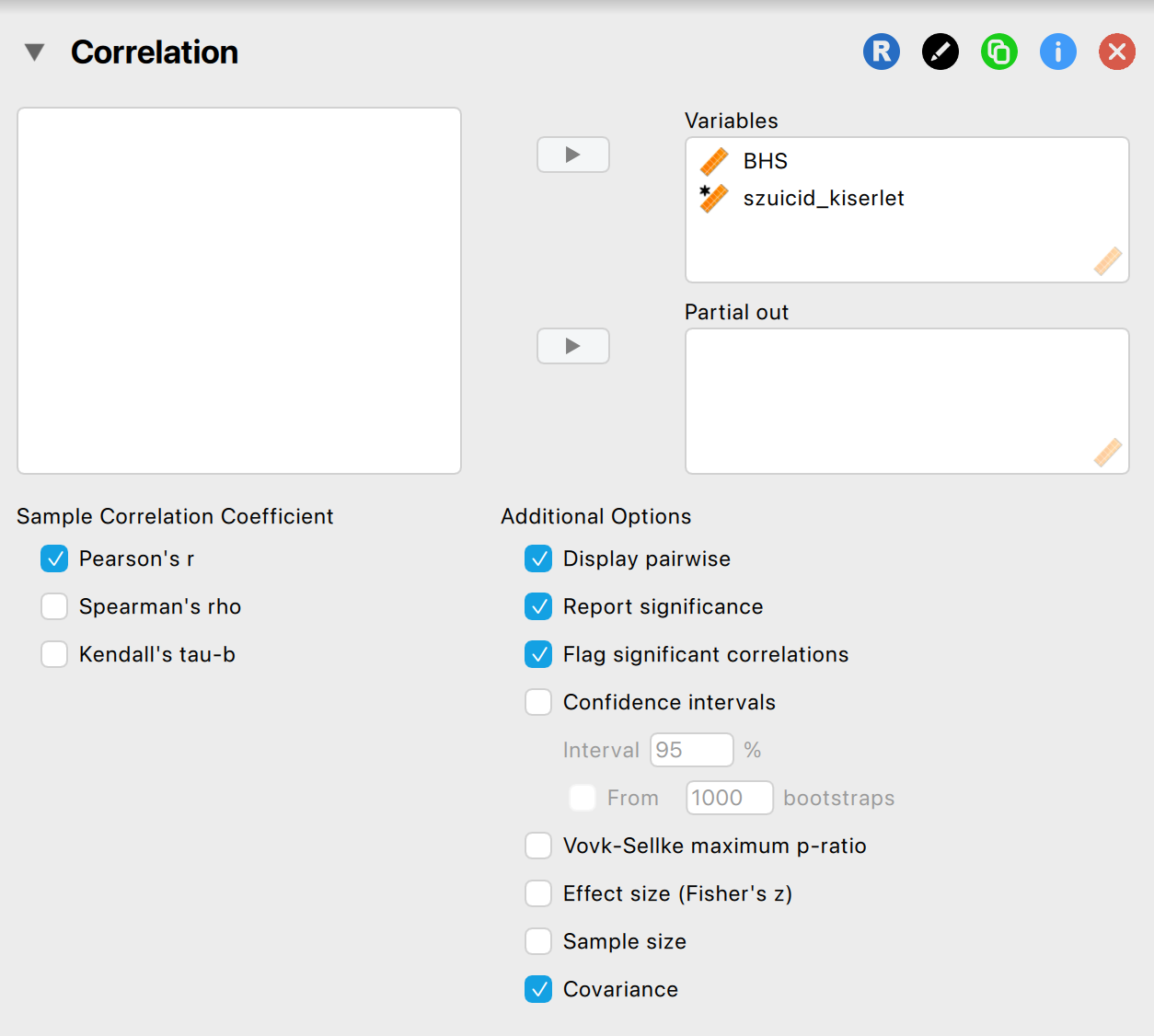
Olvassuk le az eredményt!

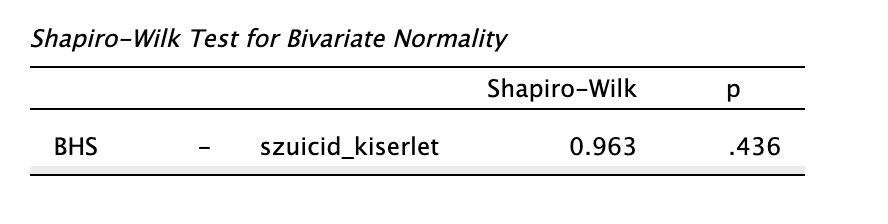
A változóink normál eloszlást követnek, mert a Shapiro-Wilk próba eredménye nem szignifikáns (p > 0,05).

Ellenőrzésképpen elvégezhetjük a függetlenmintás t-próbát (de ezt későbbi fejezetben tanuljuk).

Megoldás 5.4. Pont-biszeriális korrelációs analízist végeztünk annak feltárására, hogy van-e összefüggés a szuicid kísérletek és a Beck-féle Reménytelenség Skálán (BHS) elért pontszámok között. Statisztikailag szignifikáns, közepes-erős pozitív kapcsolatot találtunk a két változó között: r_pb(26) = 0,536, p = 0,003. Az eredmények értelmében a magasabb reménytelenség-pontszám szignifikánsan együtt jár a szuicid kísérlet előfordulásával.

5.4.3 Rang-biszeriális kapcsolat

Egy dichotóm (csak két értéket felvevő) és egy ordinális típusú változó közötti kapcsolat erősségét mutatja meg. Leggyakrabban akkor találkozunk vele, amikor nemparametrikus próbák (például Mann-Whitney U-próba) hatásnagyságát keressük.

\[ r_{rb} = 2 \times \frac{Y_1 - Y_0}{n} \]

ahol:

• n az adatpárok száma
• Y₀ és Y₁ az ordinális változó dichotóm csoportonkénti átlaga

Példa 5.5 Azt vizsgáljuk, hogy van-e összefüggés a páciensek hospitalizációs múltja (0: nem volt korábban kórházi kezelése, 1: volt már kórházi kezelése) és a funkcionális függetlenségük szintje (ordinális skála: 1 alacsony, 2 közepes, 3 magas) között (N = 45).

Az adatsor itt letölthető: korhaz_fuggetlen.sav

A rang-biszeriális korrelációhoz kicsit körmönfontan lehet hozzájutni a JASP-ban. A függetlenmintás t-próba modult kell kiválasztani, majd a dichotóm változót a csoportosító változóhoz kell behúzni, míg az ordinális változót a függő változóhoz (ne ijedjünk meg itt sem, pszeudo-skálára alakítja a JASP a változónkat). Fontos, hogy a Mann-Whitney-féle U-próbát válasszuk ki és jelöljük be a hatásnagyságot is! Az alábbi ábra szemlélteti a helyes beállítást:

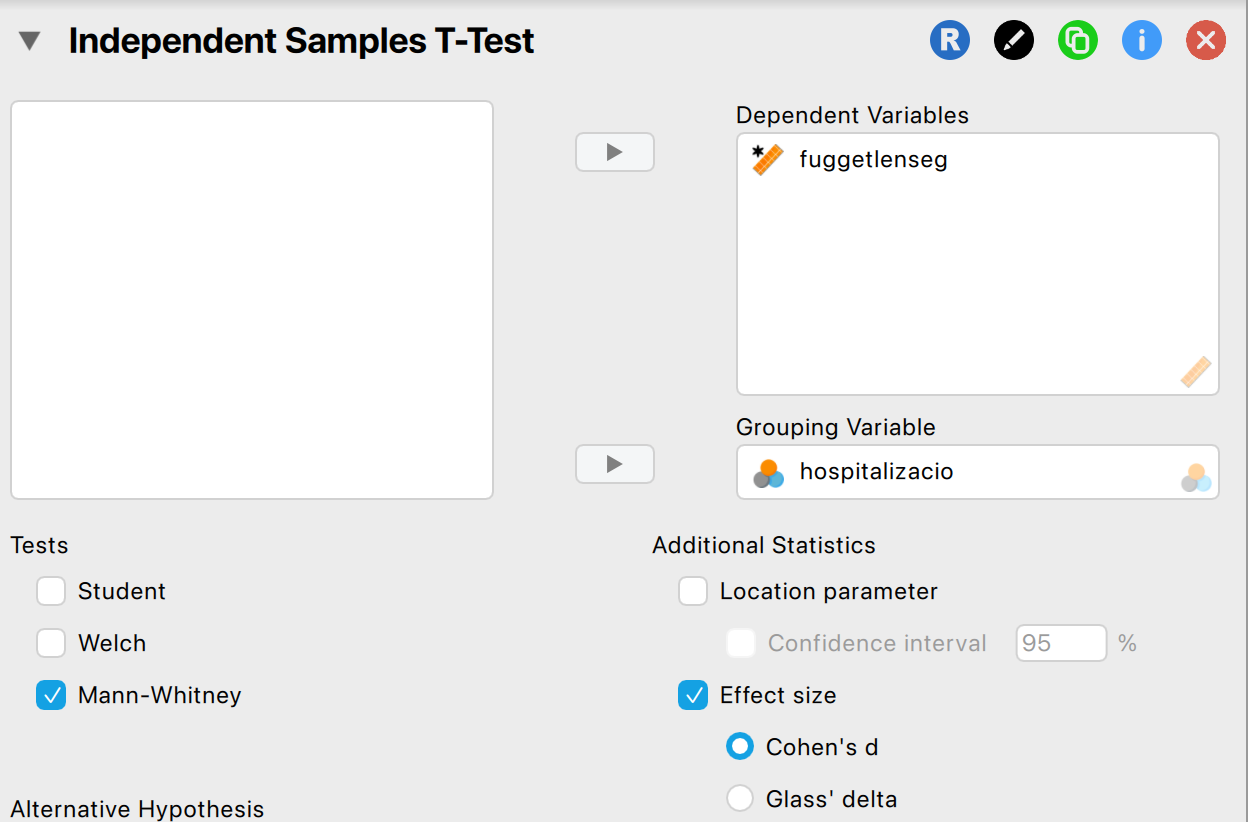
Ezt követően a Rank Biserial Correlation oszlopban lévő eredményt olvassuk le. Ez lesz a rang-biszeriális korrelációs együtthatónk.

A próba szignifikanciáját „kölcsönvesszük” a Mann-Whitney-féle U-próbától: annak a p-értékét jelentjük majd.

Megoldás 5.5. Rang-biszeriális korrelációt számítottunk a hospitalizáció és a funkcionális függetlenség közötti kapcsolat elemzésére. Az próba szignifikáns, erős negatív kapcsolatot mutatott: r_rb (43) = −0,688, p < 0,001. A korábbi hospitalizáció szignifikánsan együtt jár az alacsonyabb funkcionális függetlenséggel.

5.5 Parciális korreláció

A parciális korreláció azt vizsgálja, hogy hogyan korrelálnak a változóink abban az esetben, ha kontrollálunk egy olyan változónak a hatásával amelyik mindkét változóra hatással van. A klinikai gyakorlatban fontos, hogy a mindkét változónkra gyakorolt egyéb hatásokat mint zajokat kiszűrjük.

A parciális korreláció kiszámításához fontos megérteni a reziduálisok fogalmát. Erre utaltunk már korábban a fejezetben: a modell hibatagját (korrelációs egyenesen fekvő pontbecslések és ténylegesen mért adatpontok közötti távolságok) tekinthetjük reziduumnak. A parciális korrelációs együttható (r_xy.z) kiszámítása során

• regresszióanalízist futtatunk z változóval, hogy megbecsüljük x változót, majd kiszámítjuk a reziduálisokat (x változónak azon fennmaradó varianciája, amit z változó nem magyaráz)
• regresszióanalízist futtatunk z változóval, hogy megbecsüljük y változót, majd kiszámítjuk a reziduálisokat (y változónak azon fennmaradó varianciája, amit z változó nem magyaráz)
• az így kapott reziduumok között Pearson-korrelációt futtatunk.

Formális matematikai képlet: \[ r_{xy.z} = \frac{r_{xy} - (r_{xz} \cdot r_{yz})}{\sqrt{(1 - r_{xz}^2) \cdot (1 - r_{yz}^2)}} \]

A szemiparciális korreláció azt vizsgálja, hogy hogyan korrelálnak a változóink abban az esetben, ha kontrollálunk egy olyan változónak a hatásával amelyik csak egyik változóra van hatással.

A parciáliskorreláció-vizsgálatok esetén is fontos a normalitásvizsgálat. A JASP-ban ugyanabban a modulban érjük el a parciáliskorreláció-vizsgálatot, mint a korrelációs vizsgálatot, csak ez esetben a Partial out rovatba húzzuk a kontrollváltozónkat.

A többdimenziós normalitásvizsgálat során több adatunk jelenik meg, mint korábban:

• „All”: a többdimenziós normalitásvizsgálat eredménye, amely a kontrollváltozót is figyelembe veszi
• Conditioned: a korrelálandó változók többdimenziós normalitása a kontrollváltozó nélkül. Ha csak két fő változót korreláltatunk, akkor eredménye egybeesik majd a kétdimenziós normalitásvizsgálat eredményével
• Conditioning: a kontrollváltozó normalitása
• Residuals: a parciáliskorrelációs vizsgálatban a maradványértékek (reziduálok) többdimenziós normalitása

A fejezetben leírtak alapján, szigorú feltételek szerint akkor is, ha csak a kontrollváltozó normalitása sérül, Spearman-féle korrelációt kell futtatnunk annak ellenére, hogy akár a páronkénti normalitás nem sérül. A kutatási gyakorlatban látunk ennél megengedőbb kezelési formát, de mindenképpen indokoljuk meg a döntésünket. Érdemes összevetni a mutatókat, és főleg jelentősebb eltérések esetén a szigorúbb, robusztusabb mutatót jelenteni.

Példa 5.6 Megvizsgáljuk, hogy van-e kapcsolat az életkor és a Rövidített Beck Depresszió Kérdőív összpontszáma között a mintánkban (n = 76), ha kontrollálunk a szubjektív izoláció mértékével.

Az adatsor itt letölthető: Eletkor_BDI_izolacio.sav

Beállítjuk a próbát JASP-ban:

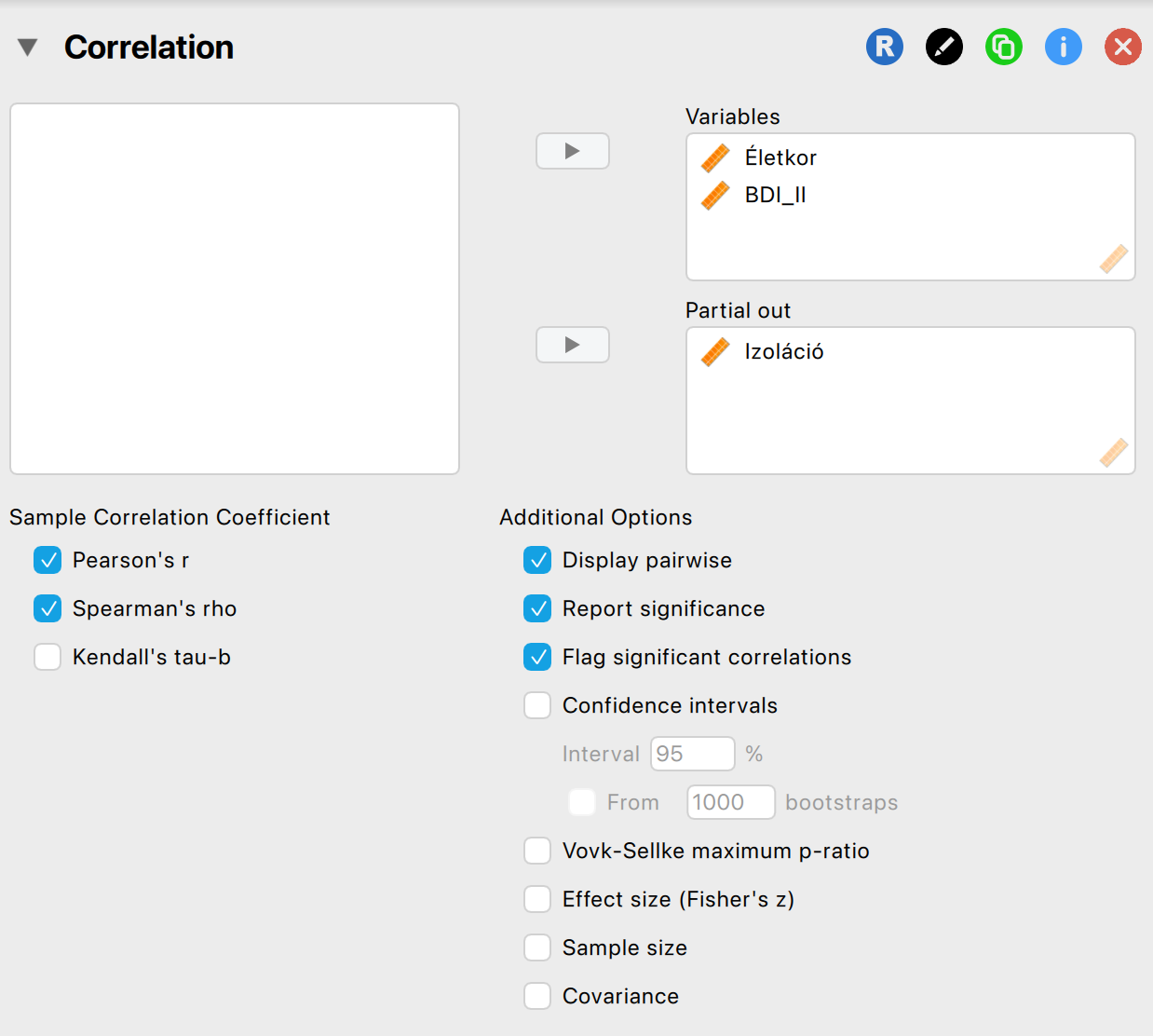
Megvizsgáljuk a normalitást:

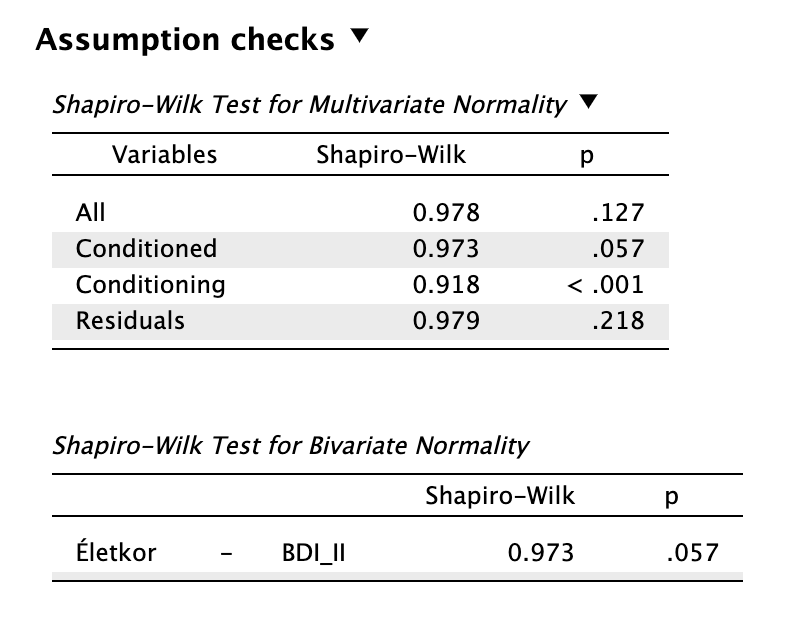
Láthatjuk, hogy a változóink páronként normál eloszlást követnek. A fő változók és a kontrollváltozó együttesen a többdimenziós normalitásvizsgálaton is megfelel, azonban önmagában a kontrollváltozó nem követi a normál eloszlást.

Leolvassuk az eremdényt:

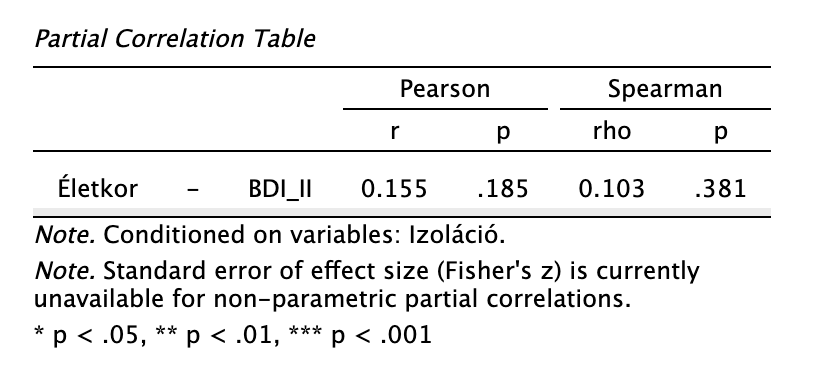
Szigorú protokollt követve a két mutató közül a Spearman-rhót vesszük figyelembe, melynek eredménye nem szignifikáns. (De a Pearson-féle korreláció sem az.)

Megoldás 5.6. Parciáliskorreláció-vizsgálatot végeztünk annak megítélésére, hogy továbbra is fennáll-e a szignfikáns összefüggés az életkor és a depresszió összpontszáma között, ha kontrolláljuk a szubjektív izoláció mértékével (N = 76). Az előzetes normalitásvizsgálat során a többdimenziós normalitás (W = 0,978, p = 0,127) és a változók páronkénti normalitása (W = 0,973, p = 0,057) teljesült. Ugyanakkor a kontrollváltozó (izoláció) eloszlása szignifikánsan eltért a normálistól (W = 0,918, p < 0,001). A normalitás részleges sérülése miatt a Spearman-féle parciális rangkorrelációt alkalmaztuk. Az eredmények alapján az életkor és depresszió közötti szignifikáns együttjárás eltűnt, a szubjektív izoláció mindkét változóval együttjárt mint torzító változó: r_s (73) = 0,103, p = 0,381. Az adatok alapján az életkor és a depresszió közötti összefüggést a mintában elsősorban a szubjektív izoláció mértéke magyarázza.

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2. kiad.). Academic Press.

Evans, J. D. (1996). Straightforward statistics for the behavioral sciences. Thomson Brooks/Cole Publishing.

Funder, D. C., & Ozer, D. J. (2019). Evaluating Effect Size in Psychological Research: Sense and Nonsense. Advances in Methods and Practices in Psychological Science, 2(2), 156–168. https://doi.org/10.1177/2515245919847202

Gignac, G. E., & Szodorai, E. T. (2016). Effect size guidelines for individual differences researchers. Personality and Individual Differences, 102, 74–78. https://doi.org/https://doi.org/10.1016/j.paid.2016.06.069

Hemphill, J. F. (2003). Interpreting the Magnitudes of Correlation Coefficients. American Psychologist, 58(1), 78–79. https://doi.org/10.1037/0003-066X.58.1.78

Lovakov, A., & Agadullina, E. R. (2021). Empirically Derived Guidelines for Effect Size Interpretation in Social Psychology. European Journal of Social Psychology, 51(3), 485–504. https://doi.org/10.1002/ejsp.2752

Perczel Forintos Dóra (Szerk.). (2018). Kérdőívek, becslőskálák a klinikai pszichológiában (4. kiad.). Semmelweis.

---

1. Bár kérdés, hogy hiányosan vagy rosszul szerkesztett kutatások állnak-e a háttérben inkább, mintsemhogy Cohen volt túl szigorú. - A szerző (F.R.) saját ítélettel töltött véleménye.

2. A tapasztalat azt mutatja, hogy sok hallgató nagyon fél valamiért a Spearman-féle együtthatót választani a Pearson-féle helyett.