6 Egyszerű lineáris regressziós vizsgálatok
Míg a korrelációs vizsgálatok nem feltételeznek „irányt” a változók között (tehát rxy = ryx), addig a lineáris regressziós vizsgálatok pont azt szeretnék kimutatni, hogy a független változó varianciája hogyan predikálja a függő változó varianciáját.
Az egyszerű lineáris regresszió hipotézise a meredekségre:
H0: b1 = 0 és β = 0
Az egyszerű lineáris regresszió hipotézise a tengelymetszetre:
H0: b0 = 0 és α = 0
Az egyszerű lineáris regresszió formális egyenlete:
\[ y = b_0 + b_1x + e \]
ahol:
- b0: a regressziós egyenes tengelymetszete az y tengellyel
- b1: a regressziós egyenes meredeksége
- e: a hiba a ténylegesen mért értékek és a regressziós egyenes pontjai (becsült értékek) között
Az egyszerű lineáris regresszió becsült értékeinek formális képlete:
\[ \begin{aligned} \hat{y} &= b_0 + b_1x \\ \text{ahol} \\ b_0 &= \bar{y}-b_1\bar{x} \\ b_1 &= \frac{\sum{(x_i-\bar{x})(y_i-\bar{y})}}{\sum{(x_1 - \bar{x})^2}} \end{aligned} \]
Amennyiben két folytonos változó lineáris kapcsolatban vannak egymással, akkor az egyik ismeretében megjósolhatjuk a másik értékét. Minél szorosabb két változó kapcsolata, annál kisebb lesz az előrejelzésünk hibája.
A regressziós modellünk az yi mért értékek alapján egy becslést hoz létre, amivel az y értékek bejósolhatók az x függvényében. Ezt a becslést a minta mért értékeire alapozza.
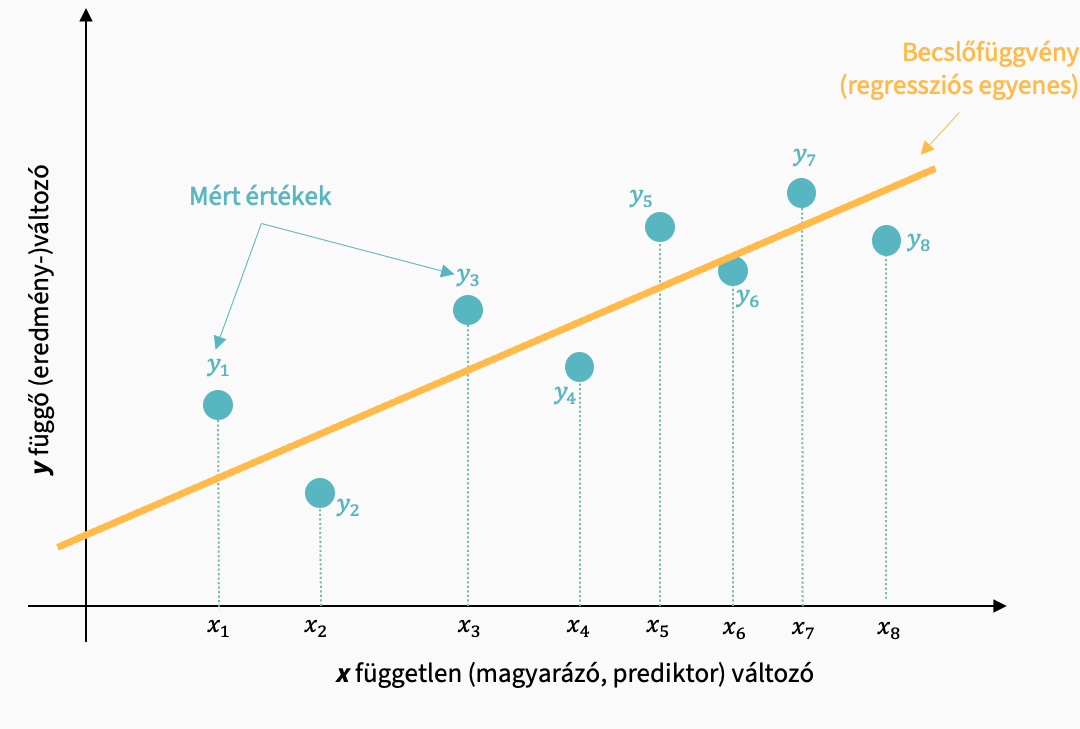
Regressziós modellünk az xi pontokhoz \(\hat{y}_i\) becsléseket rendel, amelyek a regressziós egyenesen helyezkednek el.
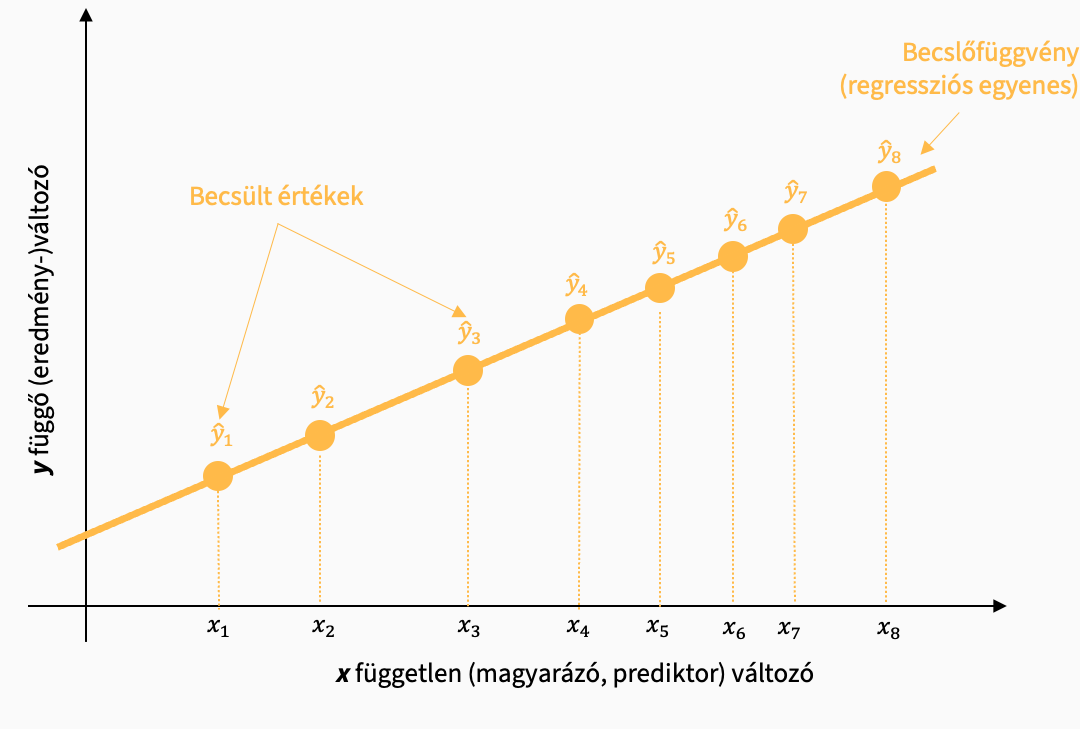
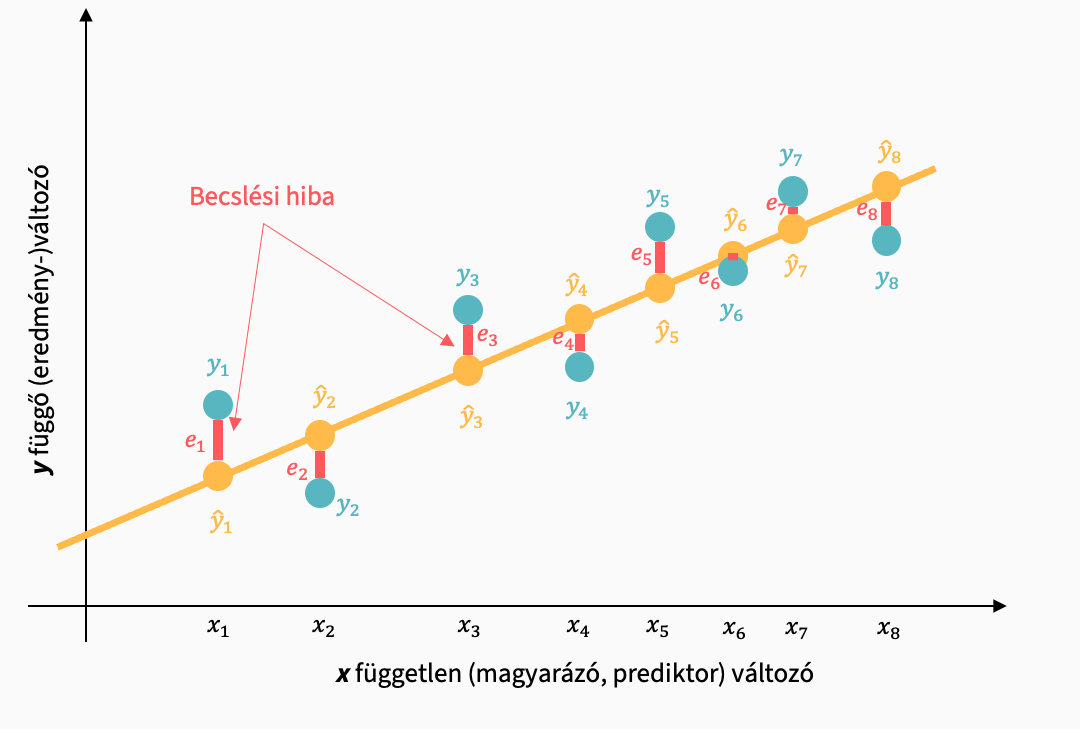
A modellünk nem magyaráz meg minden adatban fellelhető varianciát. A becsült és a ténylegesen mért értékek közötti ei becslési hiba a fennmaradó, modell által meg nem magyarázott különbség: a reziduum, maradványérték, hiba.
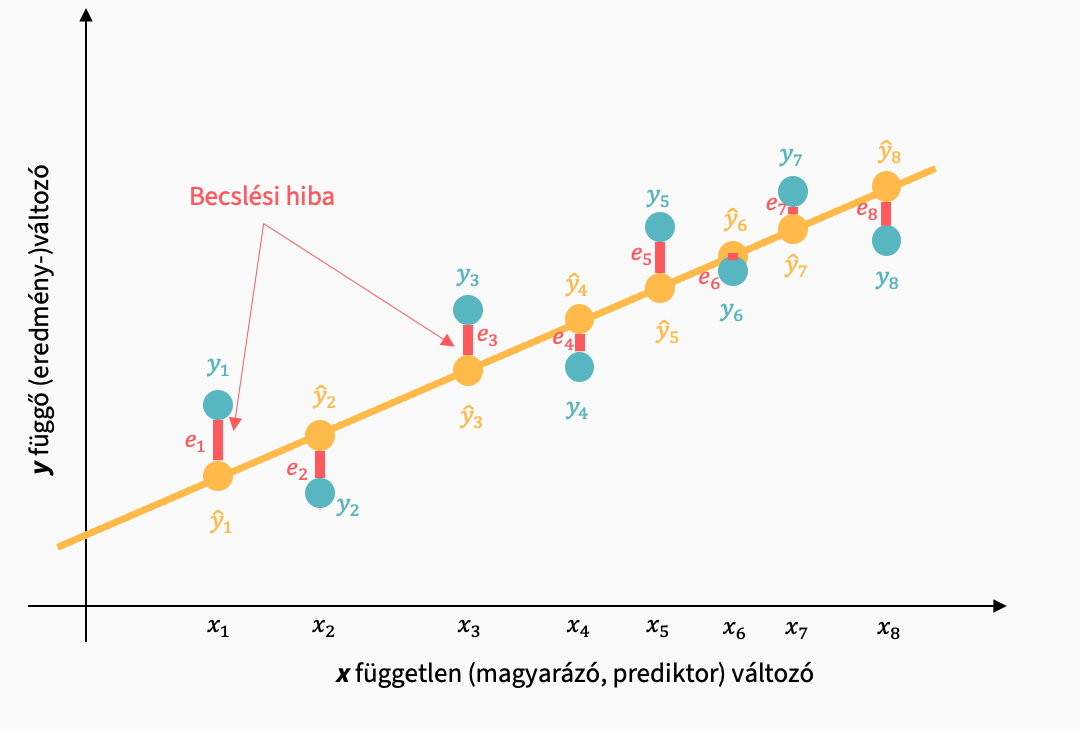
A mért értékek formálisan:
\[ y_i = \alpha + \beta x + e_i \]
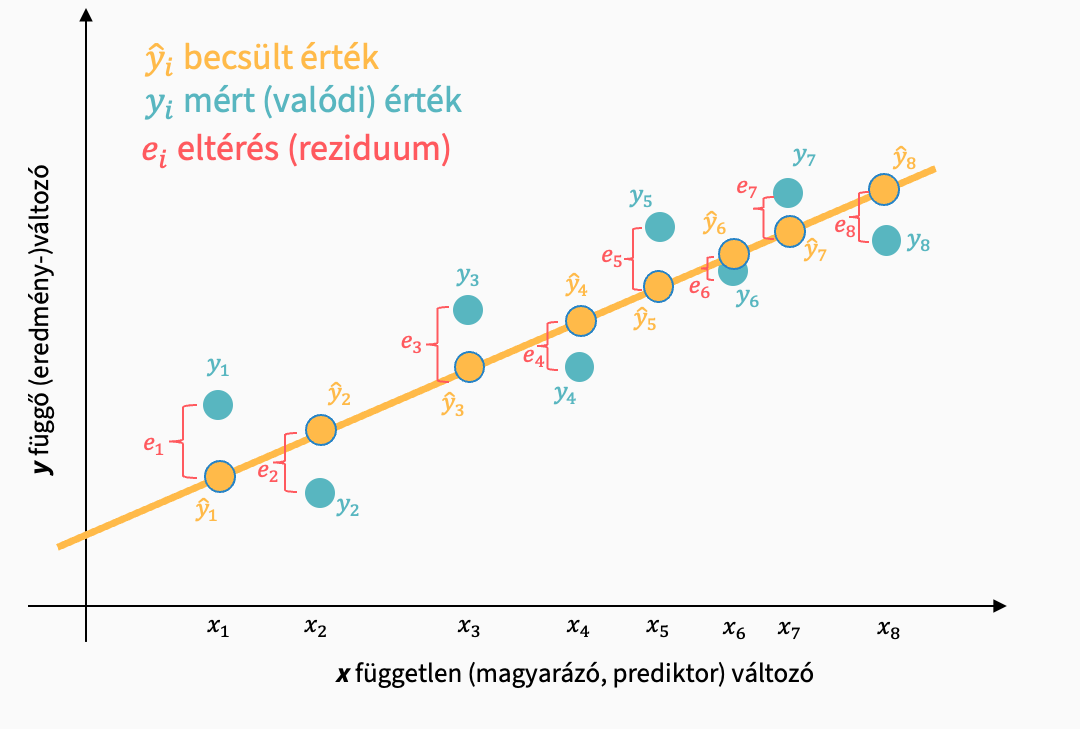
Ezek alapján képezhetünk fontos mutatókat, amiket a modellünkhöz használunk majd:
Maradványok négyzetösszege (RSS)
Megnevezések:
- Residual sum of squares (RSS) (maradványok négyzetösszege)
- Sum of squared residuals (SSR)
\[ RSS = \sum_{i=1}^n{(y_i-\hat{y}_i)^2} = \sum_{i=1}^n{e_i^2} \]
A becslés standard hibája:
\[ s_{yx} = \sqrt{\frac{\sum_{i=1}^n{e_i^2}}{n-2}} \]
Alternatív regresszióegyenesek közül azt választjuk ki majd, amelyiknél a legkisebb a maradványok négyzetösszege.
A kapcsolódó szabadságfok a \(df_R\): n - p - 1, ahol p a prediktorok száma.
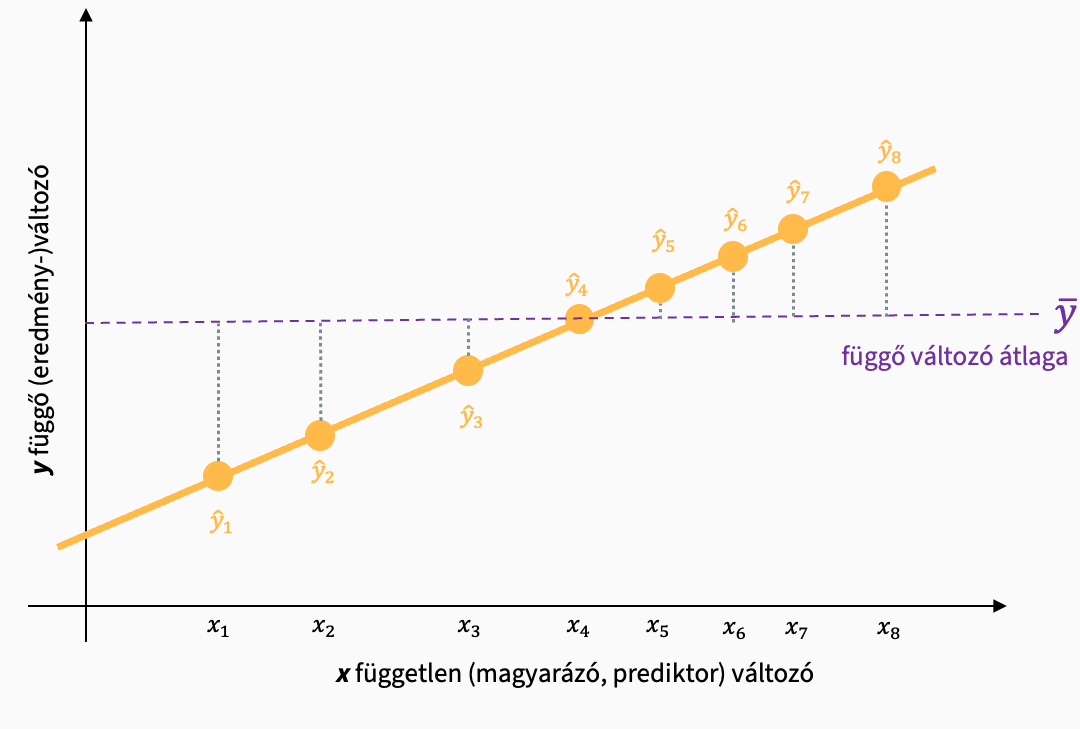
Megmagyarázott változatosság (ESS)
Megnevezések:
- Explained sum of squares (ESS) (megmagyarázott változatosság)
- Sum of squares of model (SSM)
\[ ESS = \sum_{i=1}^n{(\hat{y}_i-\bar{y})^2} \]
Azt mutatja meg, hogy a modellünk mennyire jól magyarázza átlagosan a mért adatokat.
A kapcsolódó szabadságfok a \(df_M\): p, a prediktorok száma (mert minden prediktor esetén 1 paramétert vizsgálunk, a meredekséget).
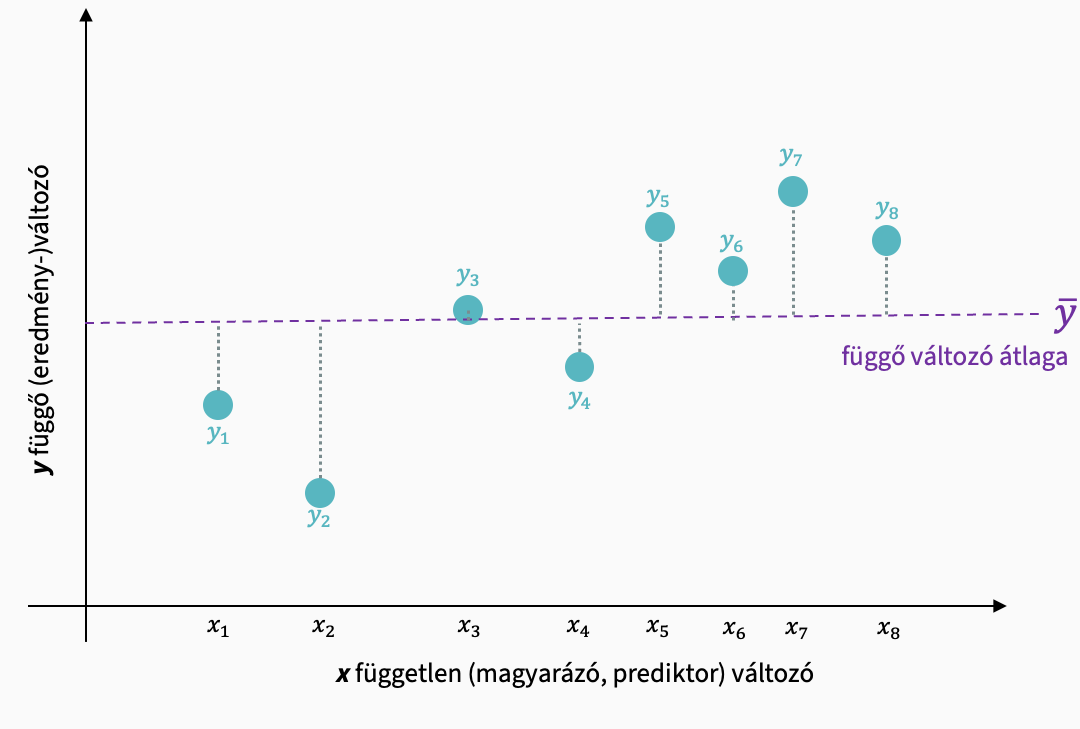
Teljes változatosság (TSS)
Megnevezések:
- Total sum of squares (TSS) (teljes változatosság)
- Sum of squares total (SST)
\[ TSS = \sum_{i=1}^n{(y_i-\bar{y})^2} \]
A mért adatok átlagtól való négyzetes eltérésével mutatja, hogy mekkora a teljes változatosság az adatokban az átlaghoz képest.
A kapcsolódó szabadságfok a \(df_T\): n - 1.
6.1 A lineáris regresszió statisztikai értéke
A statisztikai érték a hatás (modell által megmagyarázható rész) és a hiba (modell által nem magyarázható rész) aránya. Vagy máshogy kifejezve: az egy prediktorra jutó hatás és az átlagos pontatlanság hányadosa.
\[ F = \frac{\frac{ESS}{df_M}}{\frac{RSS}{df_R}} \]
Láthatjuk, hogy itt már a szabadságfokkal is operálunk.


6.2 Az ANOVA tábla értelmezése
A lineáris regressziós modellünk eredményeit több táblából olvashatjuk le. Először is meg kell vizsgálnunk, hogy a modellünk statisztikai ereje megfelelő-e, illetve szignfikáns-e. Ezt az ANOVA tábla mutatja meg.
Sematikus felépítése a következő:
| Modell | Sum of squares | df | Mean Square | F | p |
|---|---|---|---|---|---|
| Regression | SSM: Sum of squares of model | dfM = p | MSM = SSM / dfM | F = MSM / MSR | p |
| Residual | SSR: Sum of squared residuals | dfR = n - p - 1 | MSR = SSR / dfR | ||
| Total | SST: Sum of squares total | dfT = n -1 |
Észrevehetjük, hogy az F-értékhez eljutás valóban a fent leírt módszerrel történik: a különféle négyzetösszegeket arányosítjuk a szabadságfokokkal és megállapítjuk az F értéket.
A p-érték meghatározása az F-eloszlás kritikus értékén alapul. Az F-statisztikánknak két szabadságfoka van, a dfM és dfR. Tehát megkeressük, hogy milyen valószínűséggel fordul elő az F-statisztikánk értéke egy F(dfM, dfR) eloszláson.
Példa 6.1 Használjuk fel újra a parciáliskorreláció-vizsgálatnál használt adatainkat. Az adatsor itt letölthető: Eletkor_BDI_izolacio.sav. A modellben a BDI pontszám szerepel mint függő változó (y) és a szubjektív izoláció mint független változó (prediktor).
(Itt most még csak szemrevételezzük az eredményt, később megnézzük, hogyan tudjuk magunk is elvégezni a vizsgálatot JASP-ban)
| Modell | Sum of squares | df | Mean Square | F | p |
|---|---|---|---|---|---|
| Regression | \(SS_M = 551{,}702\) | \(df_M = p = 1\) | \(\begin{aligned}MS_M&=\frac{551{,}702}{1} \\ &= 551{,}702 \end{aligned}\) | \(\begin{aligned} F &= \frac{MS_M}{MS_R}\\&=\frac{551{,}702}{89{,}200} \\ &= 6{,}185 \end{aligned}\) | \(p = 0{,}015\) |
| Residual | \(SS_R = 6600{,}825\) | \(\begin{aligned}df_R &= n - p - 1 \\&= 76 - 1 - 1 \\ &= 74 \end{aligned}\) | \(\begin{aligned}MS_R &= \frac{SS_R}{df_R} \\ &= \frac{6600{,}825}{74} \\ &= 89{,}200 \end{aligned}\) | ||
| Total | \(\begin{aligned}SS_T &= SS_M + SS_R \\ &= 551{,}702 \\&+ 6600{,}825 \\ &= 7152{,}526\end{aligned}\) | \(\begin{aligned}df_T &= n -1 \\ &= 76-1 \\ &= 75\end{aligned}\) |
A p-érték azt mutatja meg, hogy mennyi a valószínűsége az F = 6,185 értéknek egy F(1, 75) eloszláson. Ez az érték pedig 0,01510695, vagyis p = 0,015. Ezt magunk is kikereshetnénk egy F-eloszlás táblázatból, vagy használhatjuk R-ben (JASP-on belül is) a következő formulát: pf(6.185, df1 = 1, df2 = 75, lower.tail = FALSE).
6.3 A lineáris regresszió hatásnagysága
A hatásnagyság arra válaszol, hogy hány százalékban tudjuk megmagyarázni az eredményváltozó (függő változó) varianciáját a független (magyarázó) változóval?
Ezt a determinációs együttható magyarázza: vagyis a megmagyarázott változatosság (mennyit magyaráz a modellünk a függő változó változatosságából) és a teljes változatosság hányadosa.
\[ R^2 = \frac{ESS}{TSS} \]


6.4 A Model Summary tábla értelmezése
A Model Summary tábla mutatja meg nekünk a modellerősségi mutatókat, amelyekre később térünk ki, de elsősorban az R, R2 és Adjusted R2 értékeket.
Az R egy Pearson-féle korrelációs együtthatóként értelmezhető, viszont a lineáris regresszió tekintetében ő kevésbé fontos, mintsem a modellünk által megmagyarázott varianciát (azaz hatásnagyságot) reprezentáló R2 mutató.
A mutató 0 és 1 között vehet fel értéket, és 100-zal megszorozva százalékos formában mutatja meg, hogy a prediktor (független) változónk hány százalékban magyarázza meg a függő változónk varianciáját. Tehát pl. R = 0,600, akkor R2 = 0,360, vagyis a független változónk 36,0%-ban magyarázza a függő változó varianciáját.
Az R2 képlete egész egyszerűen:
\[ R^2 = R \times R \]
Az Adjusted R2, magyarul a Theil-féle korrigált R2, viszont figyelembe veszi mind a mintaelemszámot, mint a bevont független (prediktor) változók számát is. Képlete:
\[ \text{Adjusted }R^2 = 1 - \frac{(1-R^2)(n-1)}{n - p - 1} \]
A korrigált R2 együtthatót ugyanúgy értelmezzük, mint az R2 együtthatót, tehát hogy hány százalékát magyarázza meg a függő változó varianciájának az összes bevont prediktor változó.
A többszörös lineáris regressziós vizsgálatoknál lesz kimondottan fontos, hogy a korrigált R2 mutatót jelentsük! Hiszen minden újabb bevont prediktor változó kicsivel növeli majd az R2 értékét, de minden újabb változó növeli a becslési hibákat, és a túl sok változó csökkenti a szabadságfokot.
Példa 6.2 Az előző példánál maradva, tekintsük meg a Model Summary táblázatot, és látjatjuk, hogy a regressziós modellünk esetén az értékek:
| Model | R | R2 | Adjusted R2 |
|---|---|---|---|
| M1 | 0,278 | 0,077 | 0,065 |
Tehát a szubjektív izoláció a depresszió pontszámok varianciájának csupán 7,7%-át magyarázza.
A korrigált R2 értéke pedig:
\[ \begin{aligned} \text{Adjusted }R^2 &= 1 - \frac{(1-R^2)(n-1)}{n - p - 1} \\ &= 1 - \frac{(1-0,077)(76-1)}{76 - 1 - 1} \\ &= 0,065 \end{aligned} \]
A korrigált R2 együtthatót ugyanúgy értelmezzük, mint az R2 együtthatót, tehát ezek alapján a szubjektív izoláció a depresszió pontszámok varianciájának csupán 6,5%-át magyarázza.
6.5 A koefficiens tábla
A harmadik táblánk a Coefficients (koefficiens) tábla, amelyben láthatjuk a lineáris regresszió elméleti mutatóit: a tengelymetszetet és a meredekséget is.
A koefficiens tábla a következő mutatókat tartalmazza:
Unstandardised, nem sztenderdizált koefficiens.
Az (Intercept) felirattal jelölt rész mutatja meg azt, hogy a regressziós egyenesünk milyen értéknél metszi az y tengelyt. Tehát ez a b0 koefficienst.
A prediktor változó nevével jelölt soron ugyanezen oszlopban azt láthatjuk a meredekséget vegyes mértékegységben. Azt mutatja, hogy ha X (prediktor változónk) 1 eredeti mértékegységnyit nő, akkor az Y (függő változónk) hány saját mértékegységnyit nő / csökken.
Standard Error, avagy a Standard hiba
Az egyes mérések bizonytalanságát leíró mutató. Minél kisebb, annál precízebb a mérésünk. Túl nagy értékű SE utalhat multikollinearitásra (többváltozós regresszióban).
Standardized, avagy a standard koefficienseink
Itt a prediktor változó nevével jelölt soron találjuk majd a β együtthatót, ami már mértékegységek nélkül (r értékhez hasonlóan sztenderd módon) mutatja meg a regressziós egyenesünk meredekségét adott változóra vonatkozóan. Ezáltal összehasonlíthatóvá válik más prediktorokkal (főleg többszörös regressziós modellek esetén).
A sztenderdizált béta-koefficiens számításának alapja a Z-eloszlás. Vagyis az adataink z-transzformáción mennek át, és ezeken az adatokon fut le a regresszió. Ha tehát z-transzformált értékeken futtatjuk le a regressziós vizsgálatot mi magunk, akkor azt tapasztaljuk majd, hogy a nemsztenderd és sztenderdizált koefficiensek egyenlőek lesznek (kivéve a tengelymetszetnél). Ez a t értéket nem változtatja meg a prediktív változó esetén (csak a tengelymetszetnél), de a standard hiba értelemszerűen változik (mert a z-transzformációval a szórás is változik a skálázás miatt).
Értelemszerűen a pozitív béta érték azonos irányú változást jelent, míg negatív béta érték esetén a prediktor változó növekedése a függő változó csökkenését jelenti.
Nagyságának értelmezése megegyezik a Pearson-féle r értelmezésével.
t és p
A t-próba értékek a nemstandard b érték és a hozzá tartozó standard hiba hányadosa:
\[ t = \frac{b}{SE_b} \]
Ha a próba szignifikáns (p < 0,05), akkor a prediktor változónk hatása nem csupán a véletlennek köszönhető. Pozitív t érték pozitív kapcsolatot jelöl, míg negatív t érték negatív kapcsolatot.
Példa 6.3 Még mindig az előző példánál maradva, tekintsük meg a koefficienseket.
| Model | Unstandardized | Standard Error | Standardized | t | p |
|---|---|---|---|---|---|
| (Intercept) | 10,015 | 2,853 | \(\frac{10{,}015}{2{,}853}=3{,}510\) | < 0,001 | |
| Izoláció | 1,238 | 0,498 | 0,278 | \(\frac{1{,}238}{0{,}498}=2{,}487\) | 0,015 |
A nemsztenderd koefficiens alapján: az izoláció 1 nyerspontszámnyi növekedése a depresszió 1,238 nyerspontszámnyi emelkedését jelzi előre. (Itt mindkét változónk mértékegysége pontszám volt, de különböző nagyságú Likert-skálákon. A lényeg az, hogy a nemsztenderd koefficiens mértékegység-tartó, tehát nem feltétlenül hasonlítható össze.)
Tehát az izoláció 1 szórásnyi növekedése a depresszió pontszám 0,278 szórásnyi növekedését jelenti.
A tengelymetszet, vagyis intercept értelmezése: ha valaki egyáltalán nem érez szubjektív izolációt (izoláció pontszáma = 0), a modellünk alapján a becsült depresszió pontszáma mégis 10,015 lesz.
Példa 6.4 Végezzük el hát együtt a teljes elemzést JASP segítségével!
A Lineáris Regresszió modulban helyezzük el a függő és független változókat a megfelelő rovatokban:
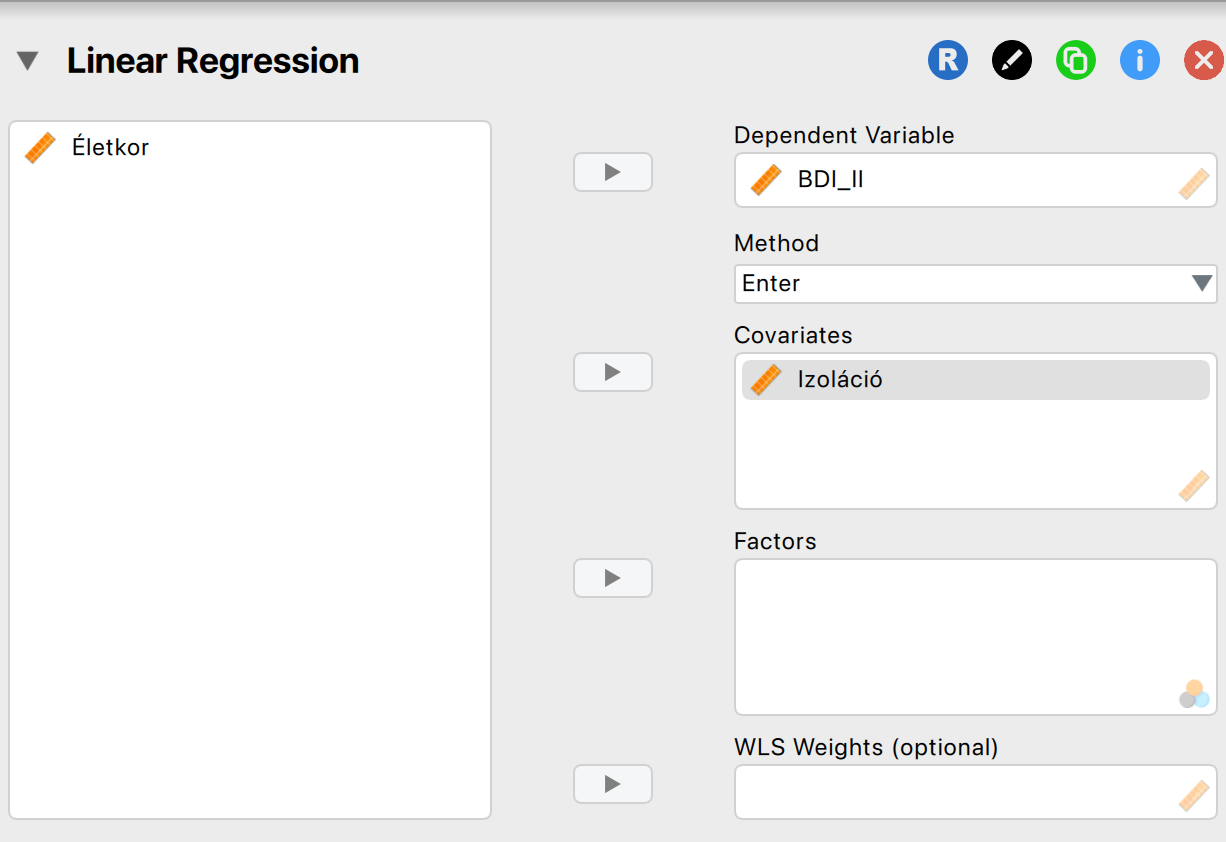
Egyszeres lineáris regresszió esetén szerencsére nem sok előfeltételt kell vizsgálnunk. Az egyetlen lényeges elem, hogy a kapcsolat lineáris legyen! Ezt ellenőrizni tudjuk, ha a maradványok lineáris alakot követnek. Ezt egy Q-Q ploton tudjuk ellenőrizni:
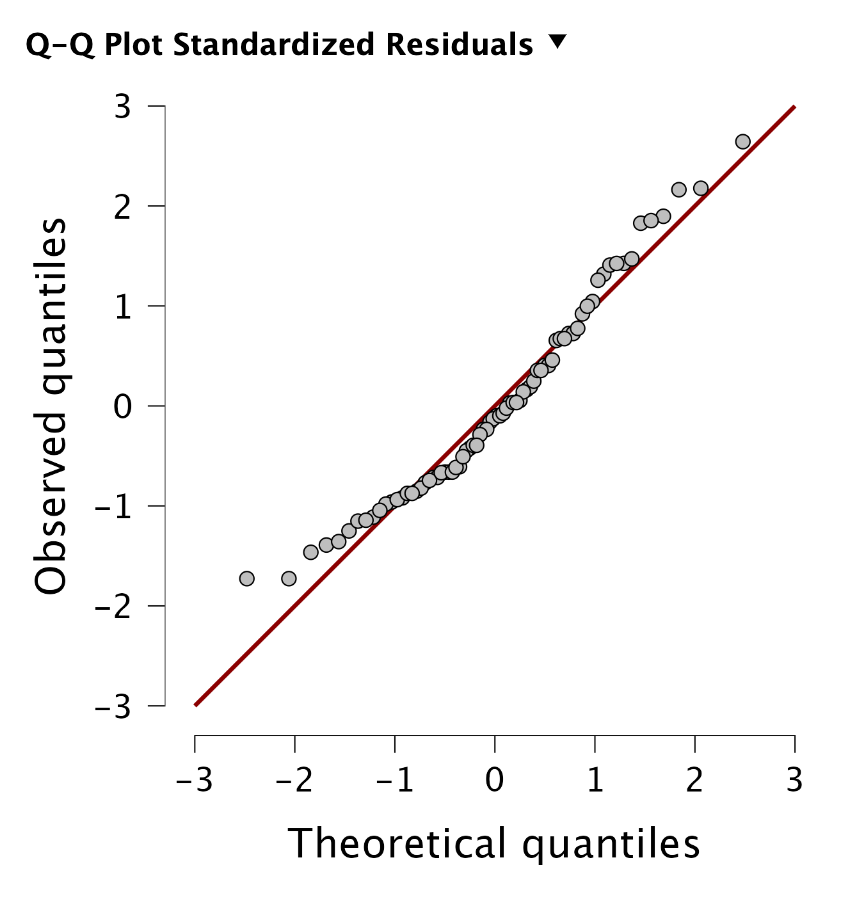
Olvassuk le az eredményt!
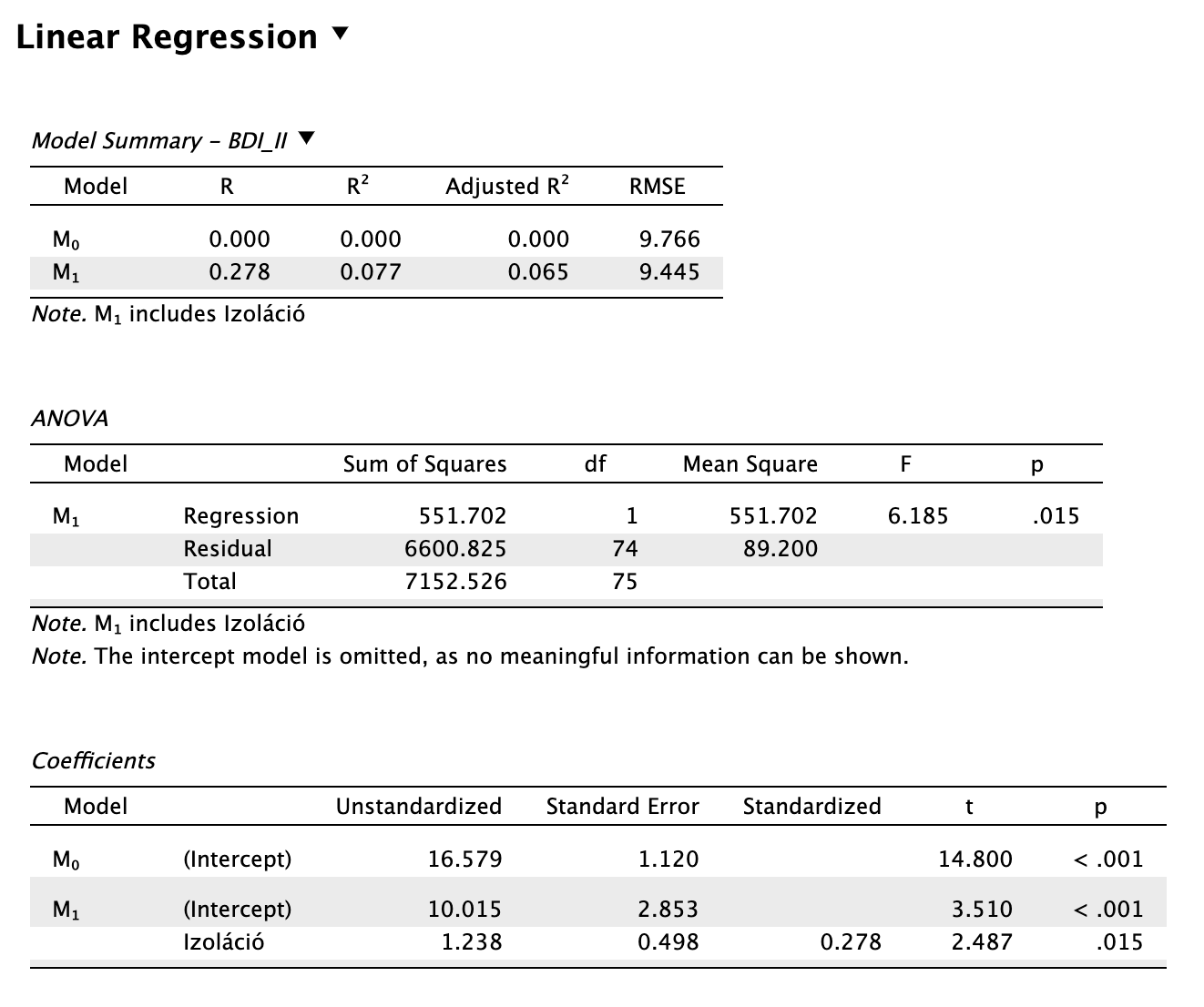
Megoldás 6.1. A szubjektív izoláció és a depresszió pontszámok közötti prediktív kapcsolatot egyszerű lineáris regresszióval vizsgáltuk (N = 76). A regressziós modell statisztikailag szignifikánsnak bizonyult: F(1, 74) = 6,185, p = 0,015. A prediktor változó a depresszió pontszámok varianciájának 7,7%-át magyarázta (R2 = 0,077, korrigált R2 = 0,065). Az izoláció statisztikailag szignifikáns, közepesen erős, pozitív prediktora a depressziónak (β = 0,278, t(74) = 2,487, p = 0,015).
(Opcionálisan jelenthető:)
A nemsztenderdizált együttható alapján az izoláció pontszámának minden egyes egységnyi növekedése a depresszió pontszám 1,238 egységnyi emelkedésével jár együtt (b = 1,238, SE = 0,498). A modell konstans értéke 10,015 volt (p < 0,001).