12  A varianciaanalízis (ANOVA) alapfogalmai

A varianciaanalízis megértéséhez frissítsük fel a tudásunkat az alábbi fogalmakról:

• variancia
• szórás
• kovariancia
• korreláció

12.1 A minták összehasonlításának elvei. A modell

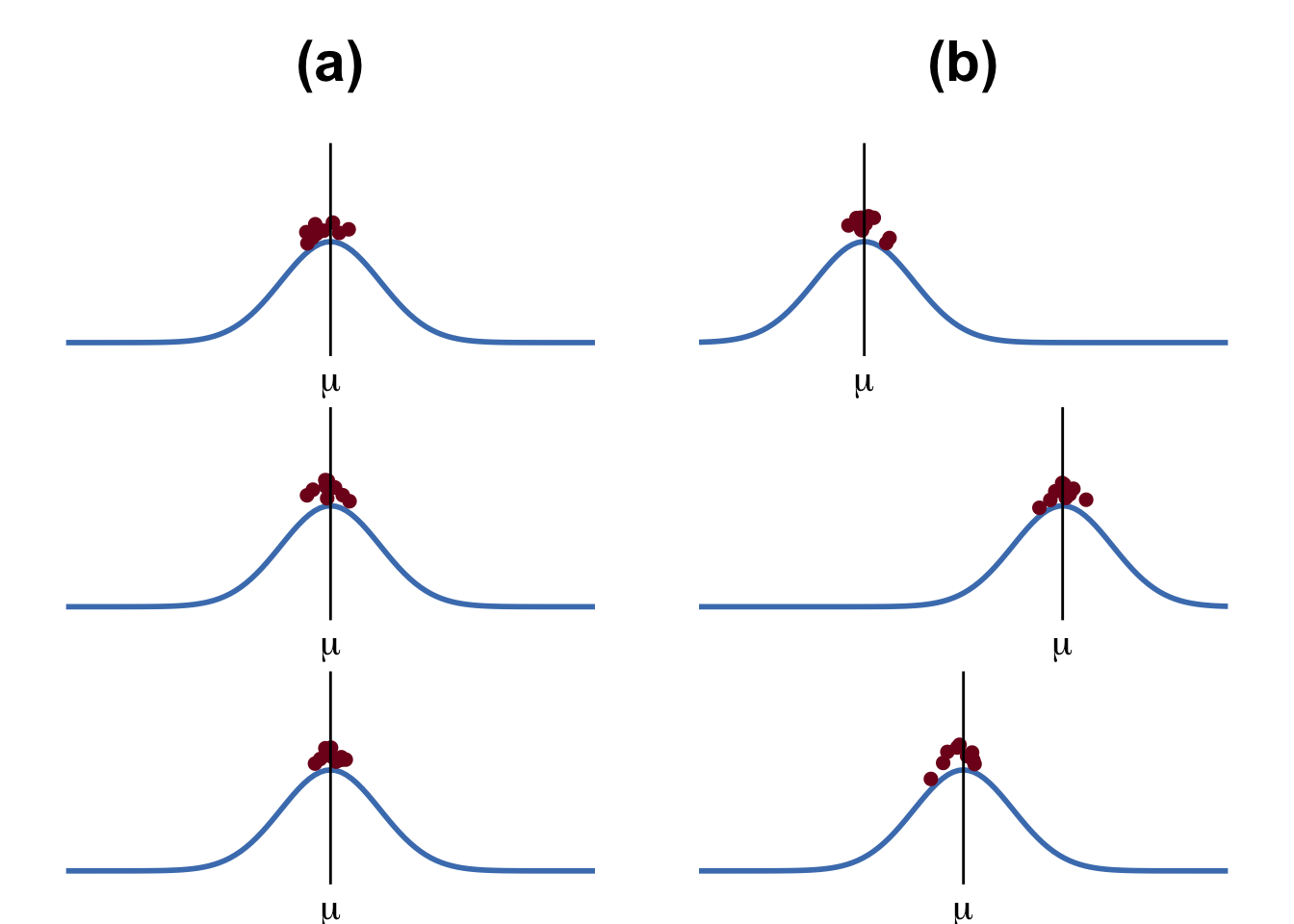
A varianciaanalízis során a t-próbákhoz hasonlóan szintén mintaátlagokat hasonlítunk össze, de ezúttal kettőnél több mintát. Az alábbi ábrán látható, hogy az (a) oszlopban lévő minták átlagai között nincs különbség, míg a (b) oszlopban lévők között van. Ezeknek a különbségeknek a meglétét és szignfikanciáját vizsgáljuk.

Az összehasonlításhoz egy lineáris regresszión alapuló referenciamodellt építünk, amely a csoportok átlagát egy grand átlagban összegzi. A függő változó összes értékét összeadjuk és elosztjuk a teljes elemszámmal:

\[ {M}_T = \frac{\sum{x_i}}{N_T} \]

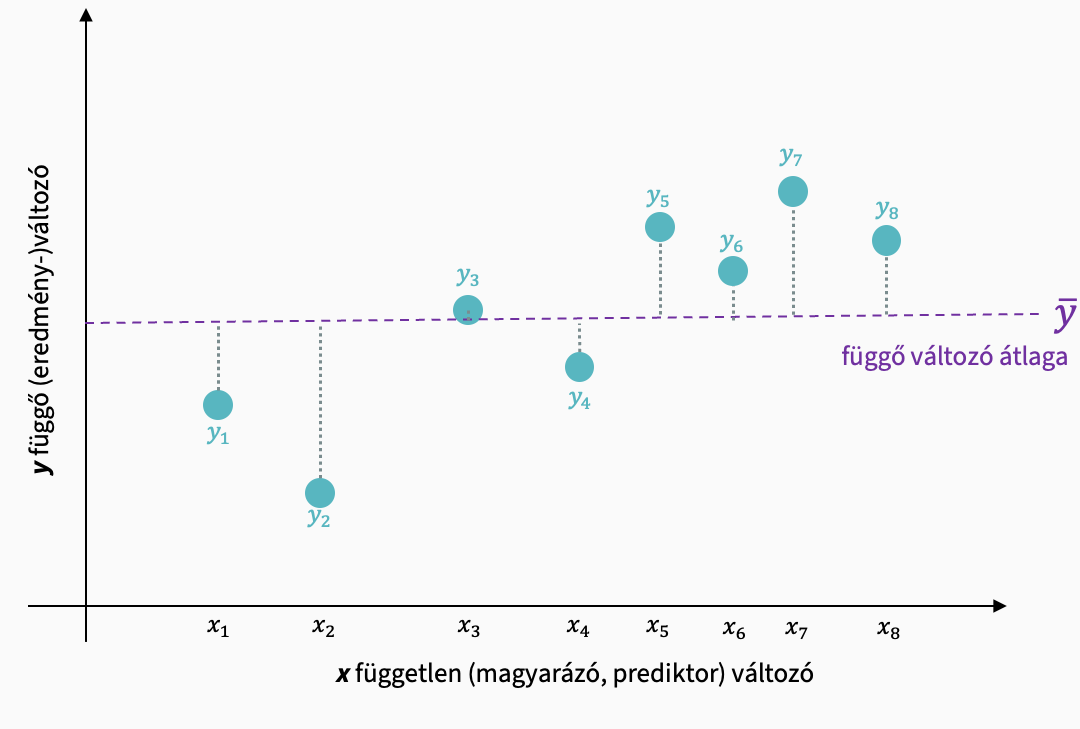
Mekkora a különbség a grand átlaggal számított predikált érték és a ténylegesen mért értékek között? Ezt a Sum of Squares Total adja meg.

SS_T: a mért pontok átlagtól való távolsága: \[ {SS}_T = \sum{(x_i - M_T)^2} \]

Lineáris regresszióban:

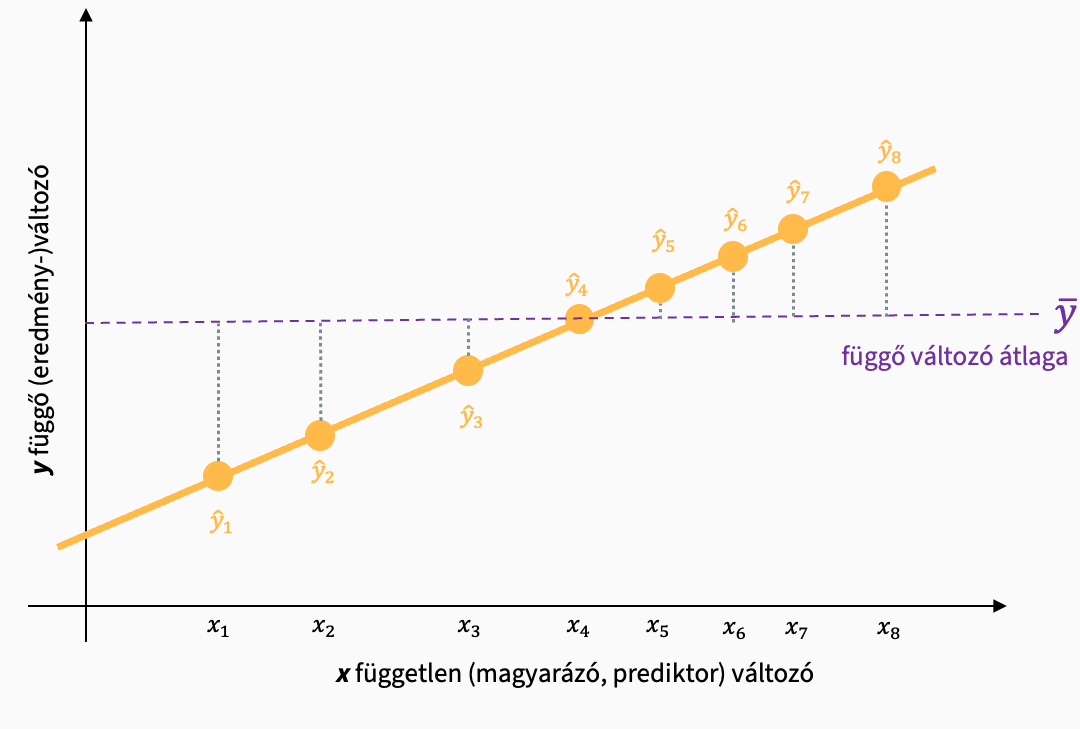
Hogy mekkora különbség van a mintaátlagok és a grand átlagok között, azt a Sum of Squares Model adja meg.

A csoportok/minták mintaátlagai:

\[ M_{csoport}=\frac{\sum{x_{csoport_i}}}{N_{csoport}} \]

SS_M: a csoportátlagok eltérése a grand átlagtól, a modell magyarázóereje

\[ {SS}_M = \sum{((M_{csoport} - M_T)^2 \times N_{csoport})} \]

Lineáris regresszióban:

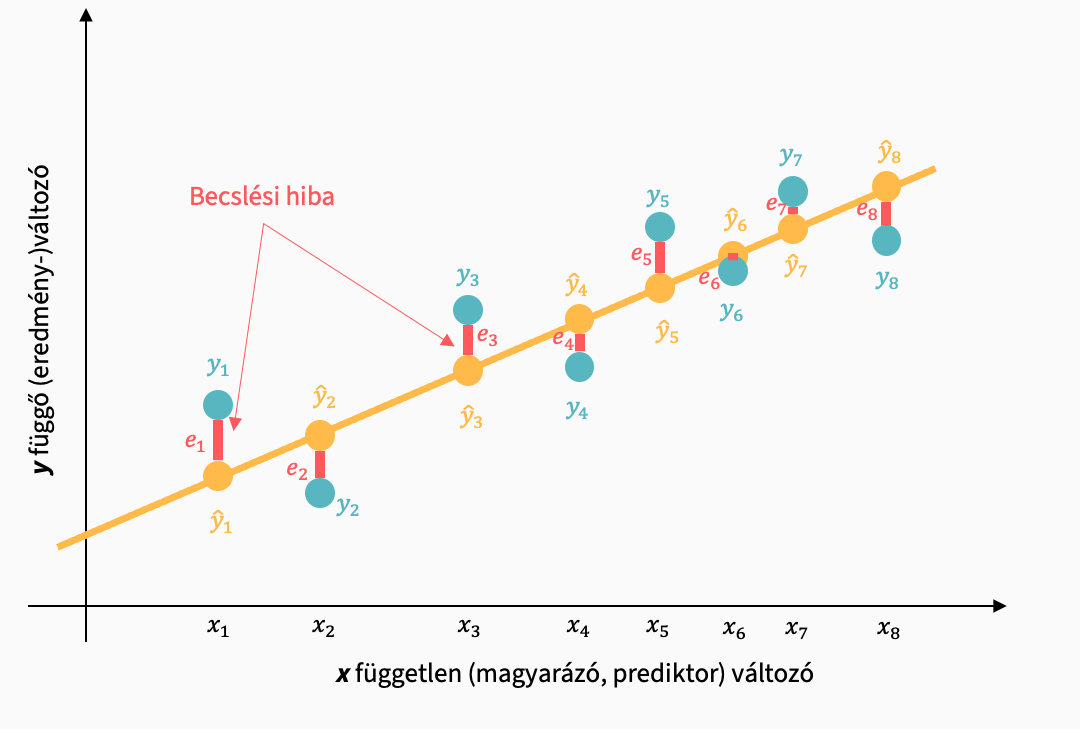
A modellel nem magyarázott variancia, a mintákon belüli eltérés, vagy más néven nemszisztematikus variancia a Sum of Squares of Residuals.

SS_R: a modell pontatlansága:

\[ {SS}_R = \sum{(x_{csoport_i} - M_{csoport})^2} \]

Lineáris regresszióban:

df_M: a modell szabadságfoka

df_R: a hiba szabadságfoka

12.2 A statisztikai érték

A lineáris regresszió során úgy beszéltünk a statisztikai értékről, hogy a hatás és hiba hányadosaként fejeztük ki. ANOVA esetén kifejezhetjük úgy is, hogy a csoportok közötti és csoporton belüli variancia hányadosaként gondolunk rá.

A statisztikai érték (F) és szignifikanciája:

\[ F = \frac{\text{hatás}}{\text{hiba}}=\frac{\frac{ESS}{df_M}}{\frac{RSS}{df_R}} \]

\[ F = \frac{\text{csoportok közötti variancia}}{\text{csoporton belüli variancia}}= \frac{\frac{SS_M}{df_M}}{\frac{SS_R}{df_R}} \]

Az omnibus F teszt azt mutatja meg nekünk nagyon leegyszerűsítve, hogy van-e szignifikáns különbség bárhol a csoportok/minták között, de nem mondja meg, hogy az hol van.

12.3 A varianciaanalízis hatásnagysága

A hatásnagyság mérése a lineáris regresszió determinációs együtthatójához hasonlóak. A megmagyarázott változatosság és teljes változatosság hányadosa ANOVA terminusokban:

\[ R^2=\frac{ESS}{TSS}=\frac{SS_M}{SS_T} \]

Ezek lesznek az \(\eta^2\) éta-négyzet, \(\omega^2\) ómega-négyzet, \(\epsilon^2\) epszilon-négyzet egyszempontos varianciaanalízis esetén, illetve \(\eta^2_p\) parciális éta-négyzet, \(\omega^2_p\) parciális ómega-négyzet, \(\epsilon^2_p\) parciális epszilon-négyzet többszempontos vagy ismételt méréses elrendezésekben (ahol az interakció vagy más faktorok hatását szeretnénk „kiküszöbölni”).

Ahogy a lineáris regressziós vizsgálatok hatásnagyságaként az R² mutatót és a korrigált R² mutatót használtuk, úgy azokat hasonlítsuk össze az ANOVA hatásnagyságokkal:

• magyarázóerő a mintában lineáris regresszió esetén (mintára vonatkozik, túlbecsüli a hatást): R²
• magyarázóerő a mintában ANOVA esetén (mintára vonatkozik, túlbecsüli a hatást): \(\eta^2\)
• magyarázóerő kimondottan a populáció becslésére ANOVA esetén: \(\omega^2\)
• magyarázóerő, ami prediktorok számával korrigál lineáris regresszió esetén: korrigált R²
• magyarázóerő, ami szabadságfokkal korrigál ANOVA esetén: \(\epsilon^2\)

12.3.1 η² éta-négyzet

A legáltalánosabban használt mutató a szakirodalomban, nagyjából az R² megfelelője. Egyszempontos (between-subjects) ANOVA esetén használhatjuk, mert a teljes varianciára vonatkoztat. Azonban torzított mutató, ezt legalább 80 éve tudjuk (Kelley, 1935). Szisztematikusan túlbecsüli a populációban lévő hatás mértékét, különösen kis minták esetén, ahogy az R² is. Emiatt a torzítás miatt a gyakorlatban inkább az ómega-négyzet javasolt (Kline, 2016), tehát a jövőbeli kutatásoknál az egyszerű éta-négyzetet mellőzzük, hacsak nem indokolt.

\[ \eta^2 = \frac{SS_M}{SS_T}= \frac{SS_M}{SS_M + SS_R} \]

Értelmezése általában Cohen (1988) alapján (hacsak nem hivatkozunk más konkrét statisztikai szakirodalomra):

• < 0,01 elhanyagolható
• 0,01-tól alacsony
• 0,06-tól közepes
• 0,14-től nagy hatásnagyság

12.3.2 ω² ómega-négyzet

Egyszempontos (between-subjects) ANOVA esetén használhatjuk. Kis mintaelemszám esetén kevésbé torzít, mint az éta-négyzet mutató. Kimondottan populációbecslésre is alkalmazható. Kimondottan ajánlott ennek a használata (Kroes & Finley, 2025).

Nem ismételt méréses használatra vonatkozó egyszerű képlet (az összes képletvariáns megtalálható Kroes & Finley (2025) cikkjében):

\[ \omega^2 = \frac{SS_M - df_M \times MS_R}{MS_R + SS_T} \]

Nagyságának értelmezése megegyezik az éta-négyzet értelmezésével.

12.3.3 ε² epszilon-négyzet

Az ómega-négyzethez hasonlóan alacsony torzítású. Egyes szimulációs vizsgálatok szerint bizonyos körülmények között pontosabb becslést adhat. Kruskal–Wallis nemparametrikus ANOVA esetén is ezt használjuk.

\[ \epsilon^2 = \frac{SS_M - df_M \times MS_R}{SS_T} \]

Nagyságának értelmezése megegyezik az éta-négyzet értelmezésével.

12.3.4 Parciális hatásnagyságmutatók

A parciális hatásnagyság-mutatókat a többszempontos elrendezésekben használjuk, ahol egyszerre több független változót és akár azok interakciójának hatását is vizsgáljuk (faktorális ANOVA). A parciális hatásnagyság-mutató egyetlen hatás (pl. A főhatás, B főhatás, vagy A x B interakció) erejét méri azáltal, hogy a nevezőből eltávolítja a többi, a modellben szereplő hatás által magyarázott varianciát.

12.3.4.1 η²_p parciális éta-négyzet

Többszempontos (faktorális) és ismételt méréses ANOVA esetén használjuk. Egy adott hatás erejét a zaj és a hatás saját varianciájához méri, figyelmen kívül hagyva a modell többi hatásának varianciáját.

Értelmezése:

• <0,02 elhanyagolható
• 0,02–től alacsony
• 0,13–tól közepes
• 0,26-tól nagy hatásnagyság

12.3.4.2 ω²_p parciális ómega-négyzet

Többszempontos ANOVA esetén használjuk, és korrigálja a parciális éta-négyzet torzítását. Ez a javasolt mutató a többszempontos elrendezésekre.

Nagyságának értelmezése megegyezik a parciális éta-négyzet értelmezésével.

12.4 Utóvizsgálatok

Az utóvizsgálatok célja, hogy megadja, hogy hol és milyen irányú eltérést találtunk a minták között. Értelemszerűen utóvizsgálat csak akkor futtatható, ha az omnibus F próbánk szignifikáns.

12.4.1 Kontraszt (a priori)

A kontrasztvizsgálatok speciális utóvizsgálatok, amit már az eredmények megtekintése és adatok megléte előtt, hipotézissel alátámasztva, előre tervezünk konkrét párok között, nem pedig minden lehetséges pár között. A kontrasztvizsgálatok során csak a hipotézisben szereplő konkrét párokat hasonlítjuk össze. Ezért a próba érzékeny, kisebb a hibainfláció, és nem kell olyan erős p-érték korrekciókat alkalmazni, mintha mindent mindennel vetnénk össze.

Többféle kontrasztvizsgálatot végezhetünk JASP-ban.

1. simple: van-e különbség a kontrollcsoport és a többi csoport között?

   Például különbözik-e a CBT és sématerápia modalitás a kontrolltól (alacsony intenzitású beavatkozás). Ennek az eredménye így jelenne meg:

   

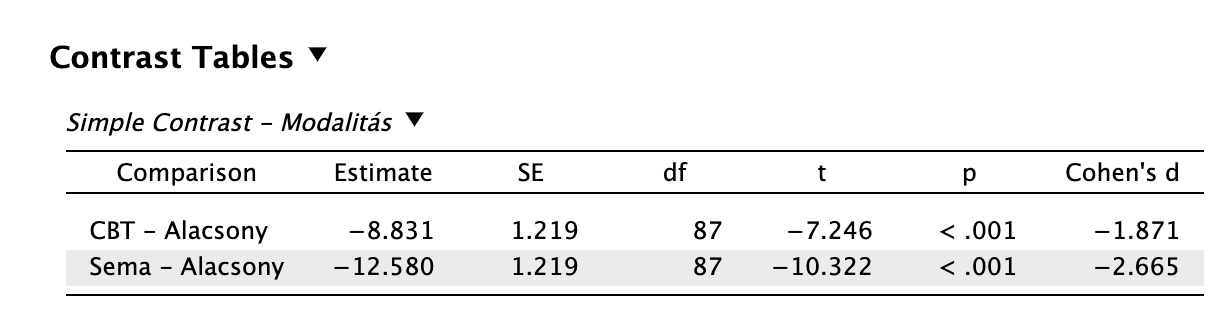
   simple contrast

   Az eredmények alapján mind a CBT, mind a sématerápia esetén alacsonyabb lesz a depresszió pontszám statisztikailag szignifikáns t-próba eredményekkel. Vagyis mindkét modalitás hatékonyabb az alacsony intenzitású terápiánál, de a kettő közül a sématerápia t-próba statisztikája és hatásnagysága alapján az ő „fölénye” markánsabb. (Ne feledjük, az előjel a különbség irányát jelöli!)

2. deviation: eltérnek-e az egyes csoportok a grand átlagtól?

   Például vizsgált pszichoterápiás modalitások eltérnek-e az „átlagos” pszichoterápiás hatékonyságtól?

   

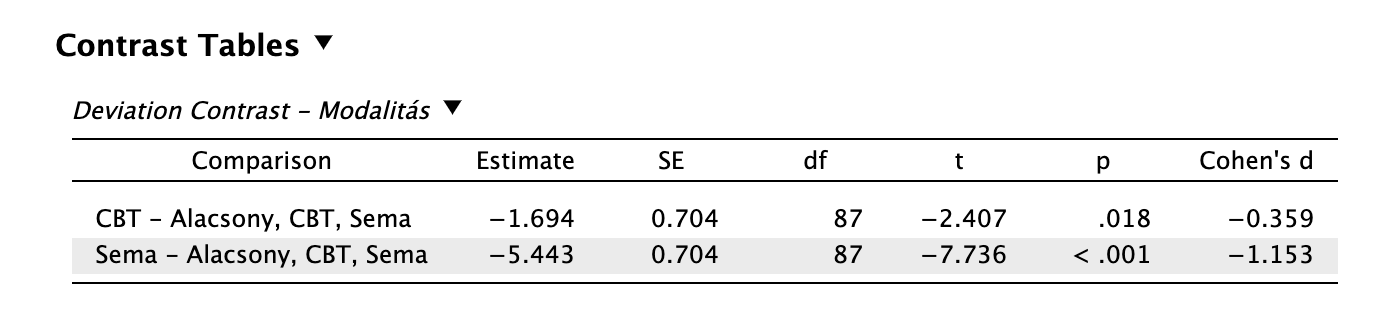
   deviation contrast

   Láthatjuk, hogy mind a CBT, mind a sématerápia hatékonyabb az átlagos pszichoterápiás hatékonyságnál. Itt is kiemelkedik a sématerápia, de a CBT is hatékonyabb egy „átlagos” pszichoterápiás beavatkozásnál.

3. difference, fordított Helmert: eltér-e az adott mintaátlag a rangsorolt csoportokban az alacsonyabb rangsorúak átlagától? Valójában ez egy kumulatív kontraszt.

   Például az adatainkban az 1-es kód az Alacsony intenzitás, 2-es kód a CBT, 3-as kód a Sématerápia. A difference módszer azt vizsgálja majd, hogy az Alacsony intenzitású terápiánál jobb-e a CBT, valamint hogy a Séma jobb-e, mint az „előző kettő átlaga”.

   

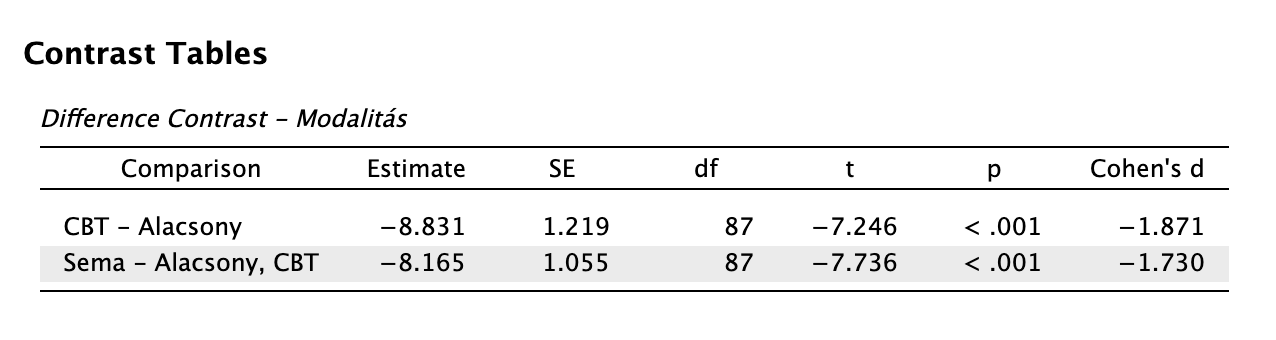
   difference contrast

4. repeated: van-e különbség az egymást követő szintek között?

   Például egyre növekvő alváshiány esetén an-e különbség a reakcióidőben?

   

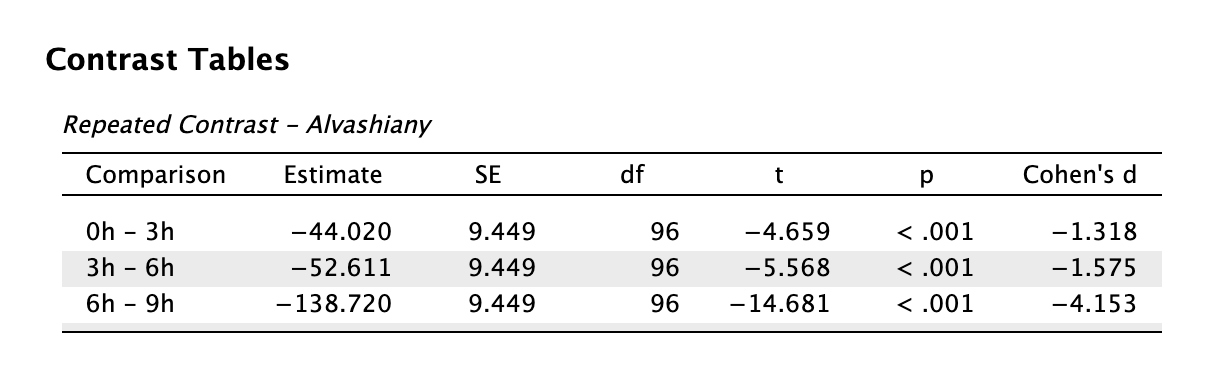
   repeated contrast

   Láthatjuk, hogy már 3 óra alvásmegvonás szignifikáns romlást okoz, nem beszélve a többi szintről. A Cohen d mutató alapján láthatjuk azonban, hogy a funkcióromlás nem egyenletes: az utolsó fázisban (6h-9h) a teljesítményromlás nagyságrendekkel rosszabb.

5. polynomial: van-e trend az adatokban?

   Például az alvásmegvonás emelésével lineárisan romlanak-e a funkciók?

   

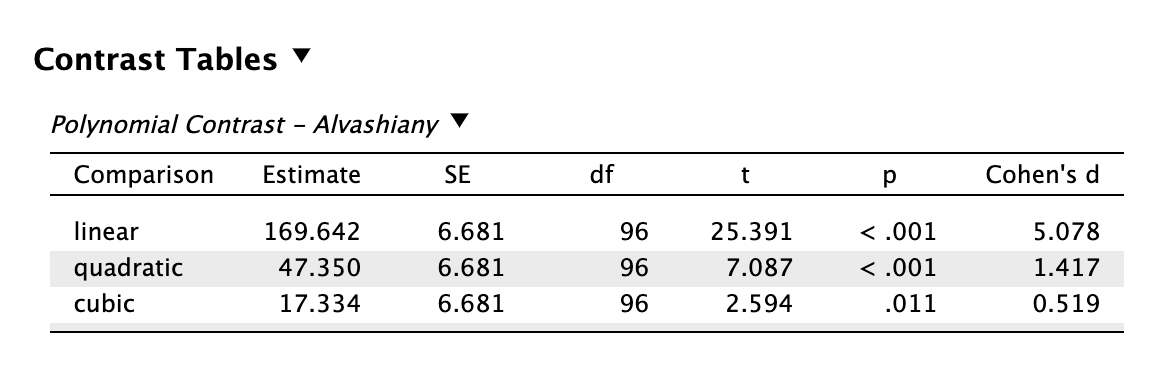
   polynomial contrast

   Láthatjuk, hogy erős a lineáris trend (linear), tehát a reakcióidő folyamatosan nő az alváshiány fokozásával. A quadratic eredmény jelzi, hogy nem egyenletes a funkcióromlás, valójában „gyorsul” (ezt sejthettük a repeated kontraszt Cohen-féle d mutatója alapján). A cubic S-alakú „hullámzást” jelez, de ez viszonylag gyengébb (saját Cohen d-k és t-statisztikák alapján).

A kontrasztvizsgálatok is t-próbák, ezért a hatásnagyságukat (Cohen d) jelentenünk kell! A fenti értelmezéseknél láthatjuk, hogy miért van erre szükség.

12.4.2 Post-hoc tesztek

A post-hoc teszt is csupán akkor végezhető el, ha az omnibus F próba eredménye szignifikáns. Post-hoc teszt során minden lehetséges párosítást megvizsgálunk, tehát exploratív elemzésekhez használjuk. Az elsőfajú hiba inflációját kiküszöbölendő különféle p-érték korrekciókat alkalmazunk, amitől viszont viszonylag kevésbé lesz érzékeny.

Aszerint kell választanunk post-hoc tesztet, hogy fennáll-e a szóráshomogenitás. A JASP felületén található post-hoc korrekciók:

Ha fennáll a szóráshomogenitás:

• Tukey HSD: a legerősebb páronkénti összehasonlító korrekció, viszont feltételezi, hogy az összehasonlítandó csoportok közel azonos méretűek és fennáll a szóráshomogenitás

  \[ {HSD} = q \sqrt{\frac{MS_R}{n}} \]

• Scheffé: az ANOVA feltételeinek sérülései esetén a javasolt korrekció, mert robusztus, és a legszigorúbb. Egyéb esetben főleg komplex összehasonlítások esetén használjuk.

  \[ {SS_{comp}} = \frac{(\sum{c_i\bar{X}_i})^2}{\sum{\frac{c_i^2}{n_i}}} \]

• Bonferroni: elosztja az alpha szintet az összehasonlítások számával (n). Növeli a másodfajú hibát, miközben az elsőfajú hiba problémáját megoldja. Nem javaslom a használatát, de gyakori korrekció az SPSS-hez szokott kutatóknál.

  \[ \frac{\alpha}{n} \]

• Šidák: a minták függetlenségét feltételezi és jobban korrigál, mint a Bonferroni. Ha a kettő közül kell választani, inkább ezt válasszuk.

  \[ 1 - (1 - \alpha)^{\frac{1}{n}} \]

• Holm korrekciót alkalmazunk ismételt méréses varianciaanalízis során (repeatead measures ANOVA) használjuk.

Ha nem áll fenn a szóráshomogenitás:

• Games-Howell: Eredetileg a Tukey-féle HSD nemparametrikus megfelelője¹.

Dunett: A Dunnett T3 próbát javasoljuk minden esetben, amikor a mintaelemszámok nem illesztettek a csoportok között és nem áll fenn a szóráshomogenitás, és még az elemszám is alacsony (n < 50). De ellentétben a címkével, a JASP 0.95 változatban nem ez a nemparametrikus Dunnet T3 próba érhető el, hanem a kontrollcsoporthoz viszonyító kétoldalú parametrikus Dunnett t-próba.

Kiegészítés 12.1 (Miért van szükség varianciaanalízisre? Miért nem használhatok egyszerűen több t-próbát?). A t-próba esetén csak két mintát tudtunk összehasonlítani: pl. kapott XY diagnózist vagy nem. Sokszor előfordul azonban, hogy több, mint két mintát kell összehasonlítanunk. Például iskolai végzettség, több kísérleti helyzet, társadalmi nemek esetén (nő, féfi, nembináris) stb.

A gond ott keletkezik, hogy két (független vagy összefüggő) minta esetén az elsőfajú (α) hiba valószínűgégét 5%-on szeretjük korlátozni a pszichológiai-szociológiai vizsgálatokban. Ez azt jelenti, hogy \(1 - \alpha = 1 - 0{,}05 = 0{,}95\) az esélye annak, hogy nem követünk el elsőfajú hibát.

Azonban több csoport összehasonlítása esetén az elsőfajú hiba valószínűsége többszöröződik, ezt hívjuk family-wise errornak.

Például 3 végzettségi csoport (alapfokú, középfokú, felsőfokú) esetén eleve 3 db t-próbát kellene végeznünk: alapfokú-középfokú, alapfokú-felsőfokú, középfokú-felsőfokú. Az esélyek így alakulnak (az összehasonlítások darabszáma szerint, nem pedig a csoportok száma szerint): \(0{,}95 \times 0{,}95 \times 0{,}95 = 0{,}95^3 = 0{,}857375\). Tehát \(1-0{,}857375=0{,}142625\), vagyis 14,3% az esélye, hogy elsőfajú hibát vétünk, szemben az eredetileg tervezett és „megengedett” 5%-kal.

Valójában nagyon gyakran 4-6 csoportot is hasonlíthatunk (és közepesen gyakran ennél is többet). Nézzük meg, hogy mekkorára nő a hiba valószínűsége csak 5 csoport esetén (pl. végzettség: alapfokú, középfokú, főiskola, egyetem, posztgraduális). Ilyenkor 10 összehasonlítást kell végezzünk:

• 1. csoport – 2. csoport (1)
• 1. csoport – 3. csoport (2)
• 1. csoport - 4. csoport (3)
• 1. csoport – 5. csoport (4)
• 2. csoport – 3. csoport (5)
• 2. csoport - 4. csoport (6)
• 2. csoport - 5. csoport (7)
• 3. csoport - 4. csoport (8)
• 3. csoport - 5. csoport (9)
• 4. csoport - 5. csoport (10)

\[ 1-0{,}95^{10} = 0{,}4012630608 \approx 40{,}1\% \]

Később láthatjuk, hogy a varianciaanalízis során, ha szignifikáns statisztikai ereje van a próbánknak (az omnibus F-próba során p < 0,05), akkor post-hoc tesztet végzünk, ami pont páronkénti t-próba. De ezeknél a próbáknál nagyon erős p-szignifikancia-korrekciókat végzünk, aminek egyéb hatásai vannak.

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2. kiad.). Academic Press.

Kelley, T. L. (1935). An Unbiased Correlation Ratio Measure. Proceedings of the National Academy of Sciences, 21(9), 554–559. https://doi.org/10.1073/pnas.21.9.554

Kline, R. B. (2016). Principles and Practice of Structural Equation Modeling (Fourth edition). The Guilford Press.

Kroes, A. D. A., & Finley, J. R. (2025). Demystifying Omega Squared: Practical Guidance for Effect Size in Common Analysis of Variance Designs. Psychological Methods, 30(4), 866–887. https://doi.org/10.1037/met0000581

---

1. Emiatt a JASP p_tukey formában jeleníti meg majd a táblázatban.