| Statistic | FELNE8 |
|---|---|
| N | 68.000 |
| Missing | 0.000 |
| Mean | 16.088 |
| SE (Mean) | 0.812 |
| SD | 6.693 |
| SE (SD) | 0.578 |
| Variance | 44.798 |
| SE (Var) | 7.740 |
| Median | 16.000 |
| Min | 2.000 |
| Max | 30.000 |
| IQR | 10.000 |
| Q1 (25%) | 11.000 |
| Q3 (75%) | 21.000 |
| Skewness | 0.022 |
| SE (Skew) | 0.291 |
| Kurtosis | -0.810 |
| SE (Kurt) | 0.574 |
| Shapiro W | 0.975 |
| Shapiro p | 0.177 |
9 Egymintás elrendezés
Az egymintás elrendezések esetén egyetlen mintát vizsgálunk, és azt hasonlítjuk össze egy ismert vagy feltételezett populációs értékkel.
Példa 9.1 Készítettünk egy kérdőíves vizsgálatot a szociális szorongásról, amelyben a Félelem a negatív megítéléstől kérdőív (Watson & Friend, 1969) legrövidebb, 8 itemes, magyar változatát (Perczel-Forintos & Kresznerits, 2017) használtuk általános és klinikai populáción, mely jó belső konzisztenciával rendelkezik (Cronbach \(\alpha\) = 0,837) és nem, életkor, végzettség és szocioökonómiai státusz tekintetében nem különbözik a hosszú változattól.
A FÉLNE-8 kérdőív itemei:
| (Szinte) soha | Néha | Rendszerint | Gyakran | (Szinte) mindig | |
|---|---|---|---|---|---|
| 1. Nyugtalanít, hogy mit gondolnak rólam az emberek, még akkor is, ha tudom, hogy ez egyáltalán nem számít. | 0 | 1 | 2 | 3 | 4 |
| 2. Gyakran tartok attól, hogy mások észreveszik a gyenge pontjaimat. | 0 | 1 | 2 | 3 | 4 |
| 3. Félek attól, hogy mások nem fognak egyetérteni velem. | 0 | 1 | 2 | 3 | 4 |
| 4. Félek attól, hogy mások megjegyzéseket fognak rám tenni. | 0 | 1 | 2 | 3 | 4 |
| 5. Amikor beszélgetek valakivel, nyugtalanít, vajon mit gondolhat rólam. | 0 | 1 | 2 | 3 | 4 |
| 6. Általában aggodalmaskodni szoktam amiatt, hogy milyen benyomást keltek. | 0 | 1 | 2 | 3 | 4 |
| 7. Időnként úgy érzem, túl sokat foglalkozom azzal, hogy mások mit gondolnak rólam. | 0 | 1 | 2 | 3 | 4 |
| 8. Gyakran aggódom amiatt, hogy valami rosszat mondok vagy teszek. | 0 | 1 | 2 | 3 | 4 |
A kérdőíves adatainkban jelöltük, ha a válaszadó rendelkezik F32.XX Depressziós epizód BNO kódú diagnózissal.
A minta főbb mutatói a FÉLNE-8 összpontszámokra vonatkozóan:
Az adatfájl letölthető: FELNE8_onesample_F32.sav
Megoldás 9.1. A vizsgálatban (N =) 68 fő vett részt, közülük 36 nő (52,9%) és 32 férfi (47,1%). A vizsgált személyek átlagéletkora (M =) 35,19 év (SD = 2,97). A mintában a szociális szorongás átlagpontszáma (M =) 16,09 (SD = 6,69). A változó normál eloszlást követ (W(68) = 0,975, p = 0,177).
9.1 Egymintás t-próba
Egymintás t-próbát abban az esetben végezhetünk, ha a mintánk átlagát szeretnénk összevetni egy ismert populációátlaggal, de a populáció szórását nem ismerjük.
Például, ha egy konkrét tesztpontszámot szeretnénk összehasonlítani az országos átlaggal a szórást nem ismerve, akkor egymintás t-próbát alkalmazhatunk.
A t-próba egy parametrikus próba, vagyis azt feltételezi, hogy a mintánk egy meghatározott eloszlást követ.
Az egymintás t-próba előfeltételei:
Skála típusú változóval dolgozunk (pl. pontszámok). Erről magunk győződünk meg.
A vizsgált változónk normál eloszlású (vagy a minta mérete elég nagy ahhoz, hogy a központi határeloszlás tétel érvényesüljön). Ezt Shapiro-Wilk teszttel ellenőrizhetjük.
A mintaelemek függetlenek egymástól. Ezt a kutatási terv alapján biztosítjuk.
A populáció szórása ismeretlen. Ha ismert, akkor z-próbát alkalmazunk.
A változó nem tartalmaz extrém értékeket. Ezt boxplot segítségével ellenőrizhetjük (vagy az IQR-módszerrel).
Kétoldalú próba esetén a nullhipotézis azt állítja, hogy a minta átlaga megegyezik a populáció ismert átlagával, míg az alternatív hipotézis szerint a két átlag különbözik egymástól.
Egyoldalú próba esetén az alternatív hipotézis szerint a minta átlaga nagyobb/kisebb a populáció ismert átlagánál.
Példa 9.2 (Példa egymintás elrendezésre csak populációátlag ismeretében) Szakirodalmi adatok alapján tudjuk, hogy a FÉLNE-8 kérdőívvel mért félelem a negatív megítéléstől átlagpontszáma 17,00 major depressziós esetén (Carleton és mtsai., 2011).1
Klinikánkon csoportot indítunk major depresszióval diagnosztizáltak részére (F32.XX), és szeretnénk megnézni, hogy az általunk mért félelem a negatív megítéléstől átlagpontszám különbözik-e a szakirodalmi átlagtól.
Állítsuk fel a hipotéziseket kétoldalú próba esetére!
- Nullhipotézis (H0): A minta átlaga megegyezik a populáció ismert átlagával (μ = 17,00).
- Alternatív hipotézis (H1): A minta átlaga különbözik a populáció ismert átlagától (μ ≠ 17,00).
Vizsgáljuk meg az előfeltételeket!
A változó skála típusú?
Igen, mert a FÉLNE-8 kérdőív Likert skála, tehát itemei ugyan ordinális változók, de a belőlük képzett összpontszám intervallumskálaként kezelhető.
A minta normál eloszlású?
Shapiro-Wilk teszttel ellenőrizzük a JASP szoftver segítségével a leíró statisztikák között vagy az egymintás próbára vonatkozó modulban az előfeltételvizsgálatok között.
A mintaelemek függetlenek egymástól?
Igen, mert a résztvevők különböző személyek, és a kutatási terv alapján biztosítottuk a függetlenséget.
A populáció szórása ismert?
Nem, a populáció szórása ismeretlen2.
A változó nem tartalmaz extrém értékeket?
Boxplot segítségével ellenőrizzük, vagy IQR módszerrel.
Állítsuk be a JASP-ban a próbát!
A hipotézis felállítását JASP-ban a következők szerint végezhetjük el:
A populáció ismert változóját (ti. átlag) beállítjuk a „Test value” mezőben
A megfelelő alternatív hipotézist jelöljük az „Alternative Hypothesis” rovatban
A Shapiro–Wilk-féle normalitásvizsgálatot az „Assumption checks” szekció „Normality” kipipálásával futtathatjuk.
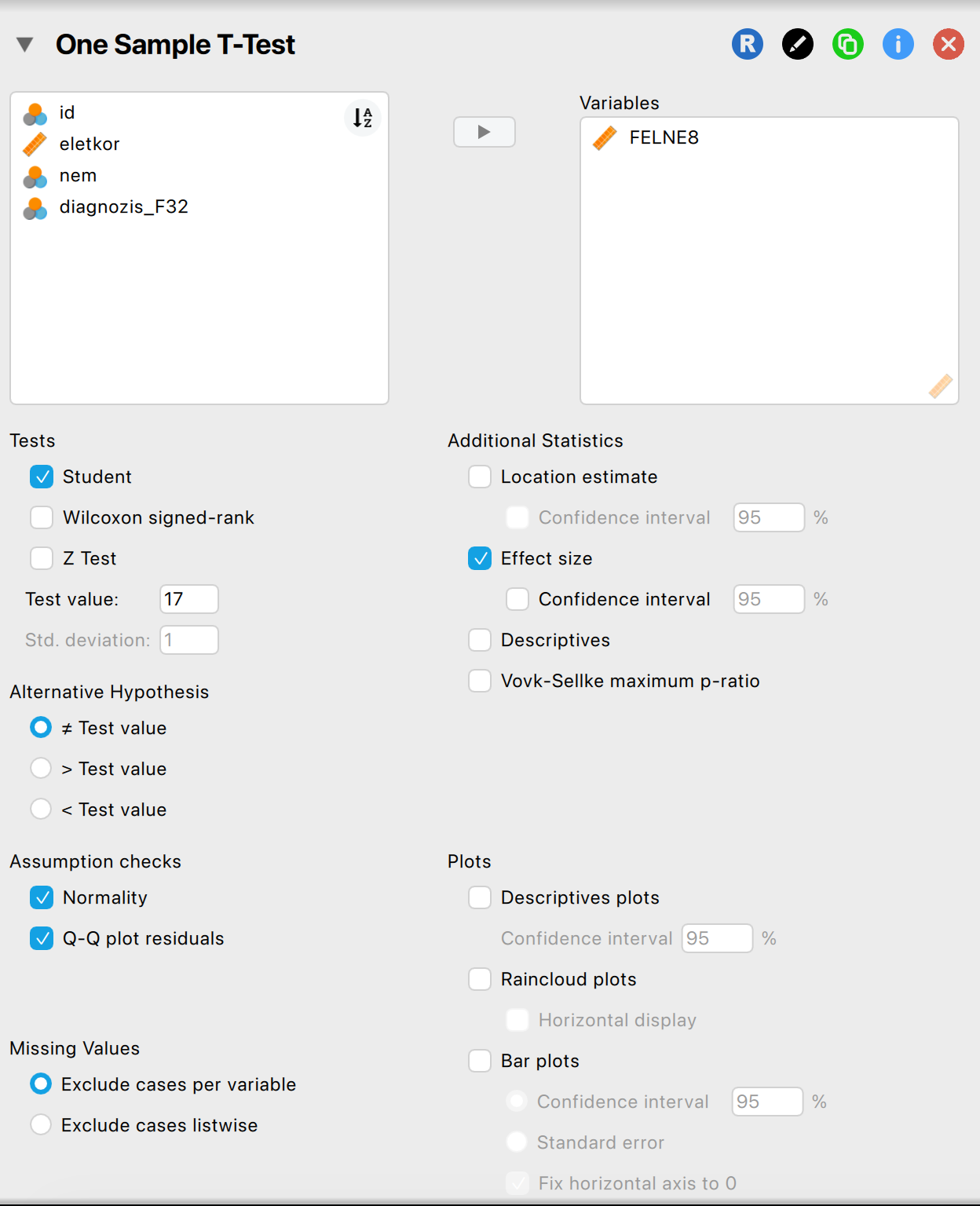
Beállítások: alternatív hipotézis, normalitásvizsgálat, hatásnagyság, tesztérték Olvassuk le és értelmezzük az eredményt!
Előfeltételvizsgálat: normalitás
Először a normalitásvizsgálat eredményeit olvassuk le. Ugyanis, ha nem követ normál eloszlást a vizsgált változónk, akkor az egymintás Wilcoxon-féle előjeles rangpróbát kellene használnunk, nem pedig a Student-féle t-próbát.
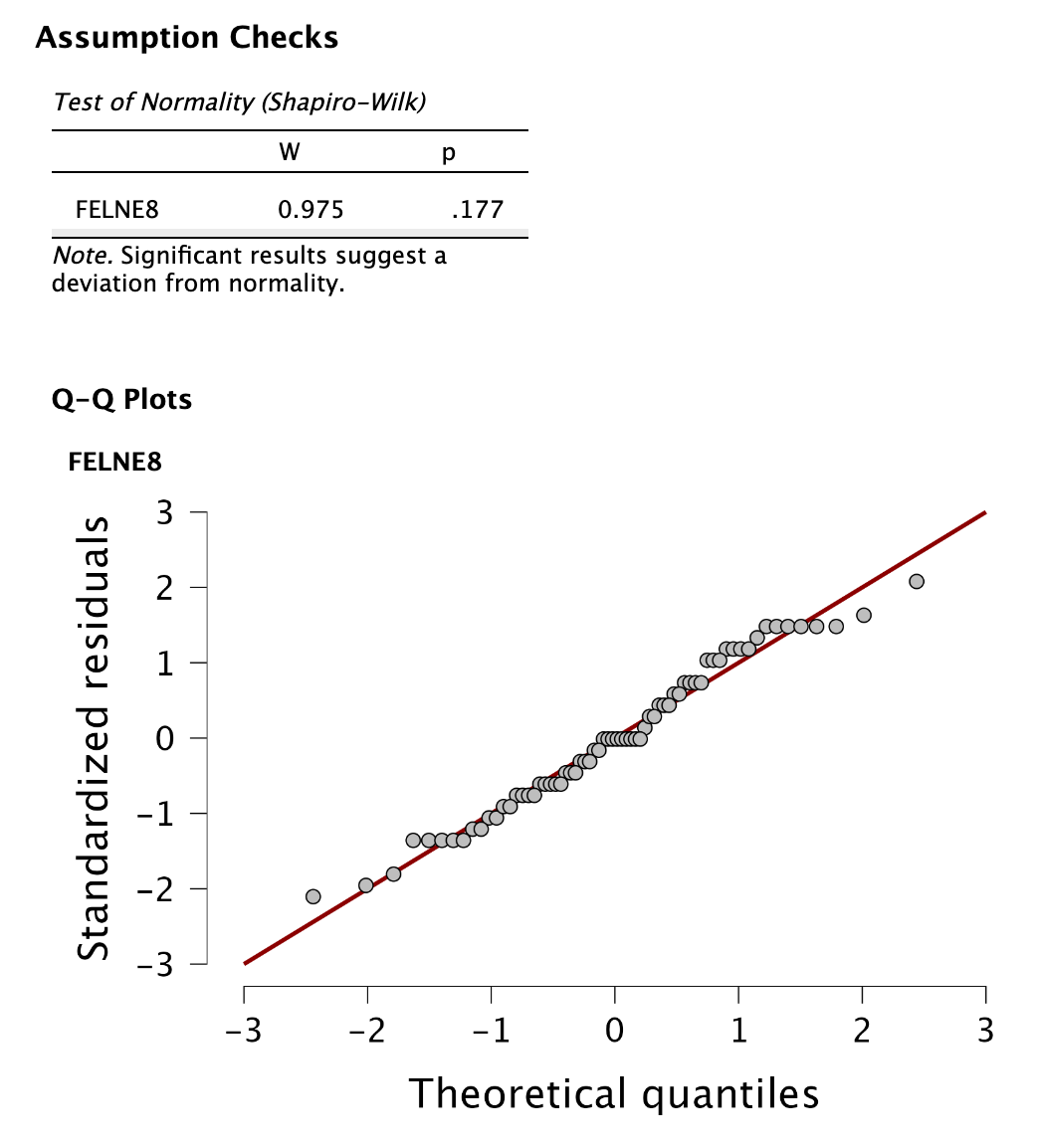
A normalitásvizsgálat eredményei Az eredményeket leolvasva láthatjuk, hogy a Shapiro-Wilk próba nem szignifikáns (azaz \(p > 0,05\)), mert 0,177. Tehát a változónk normál eloszlást követ 3.
A Q-Q plot szemrevételezése alapján látjuk, hogy az adatok legnagyobb részt a vörös színű átlón mozognak, egyértelmű alakeltérés nem észlelhető.
A t-próba eredményének leolvasása

A t-próba eredménye A JASP a megjegyzések között jelzi nekünk az alábbi fontos figyelmeztetéseket:
Student-féle t-próbát alkalmazunk (“Student’s t-test”)
Az alternatív hipotézisünk a 17,00 átlagértékhez viszonyít kétoldalasan. (“For the Student t-test, the alternative hypothesis specifies that the mean is different from 17.”)
Így tehát amit leolvasunk a táblából, az ezekkel a figyelmeztetésekkel együtt értelmezendő:
A t-próba t-statiszikája: -1,123. Hogyan jött ki?
A szabadságfok: 67,000. Ez a mintaelemszámnál eggyel kisebb érték, vagyis \(N - 1\).
A p-érték: 0,265. Tehát a próba nem szignifikáns, vagyis \(p > 0,05\). Hogyan jött ki?
Cohen-d hatásnagyság: -0,136. Ez Cohen (1988) alapján elhanyagolható mértékű hatásnagyság.
Megoldás 9.2. A mintánk átlaga (M = 16,09, SD = 6,69) nem tér el szignifikánsan a norma szerinti 17,00-s értéktől (t(67) = -1,123, p = 0,265, d = -0,136).
Kiegészítés 9.1 (Az egymintás t-próba t-értékének kiszámítása). \[ t = \frac{\bar{x} - \mu_0}{\frac{s}{\sqrt n}} = \frac{\bar{x} - \mu_0}{SEM} \]
ahol
\(\bar{x}\) a mintánk átlaga (= 16,088),
\(\mu_0\) az ismert populációátlag (= 17,00),
\(s\) a mintánk szórása (= 6,693),
\(\sqrt n\) pedig a mintaelemszám négyzetgyöke (= 8,246).
Ez utóbbi két elem hányadosa a standard hiba (SEM).
Az egyenlet eredménye: -1,123331.
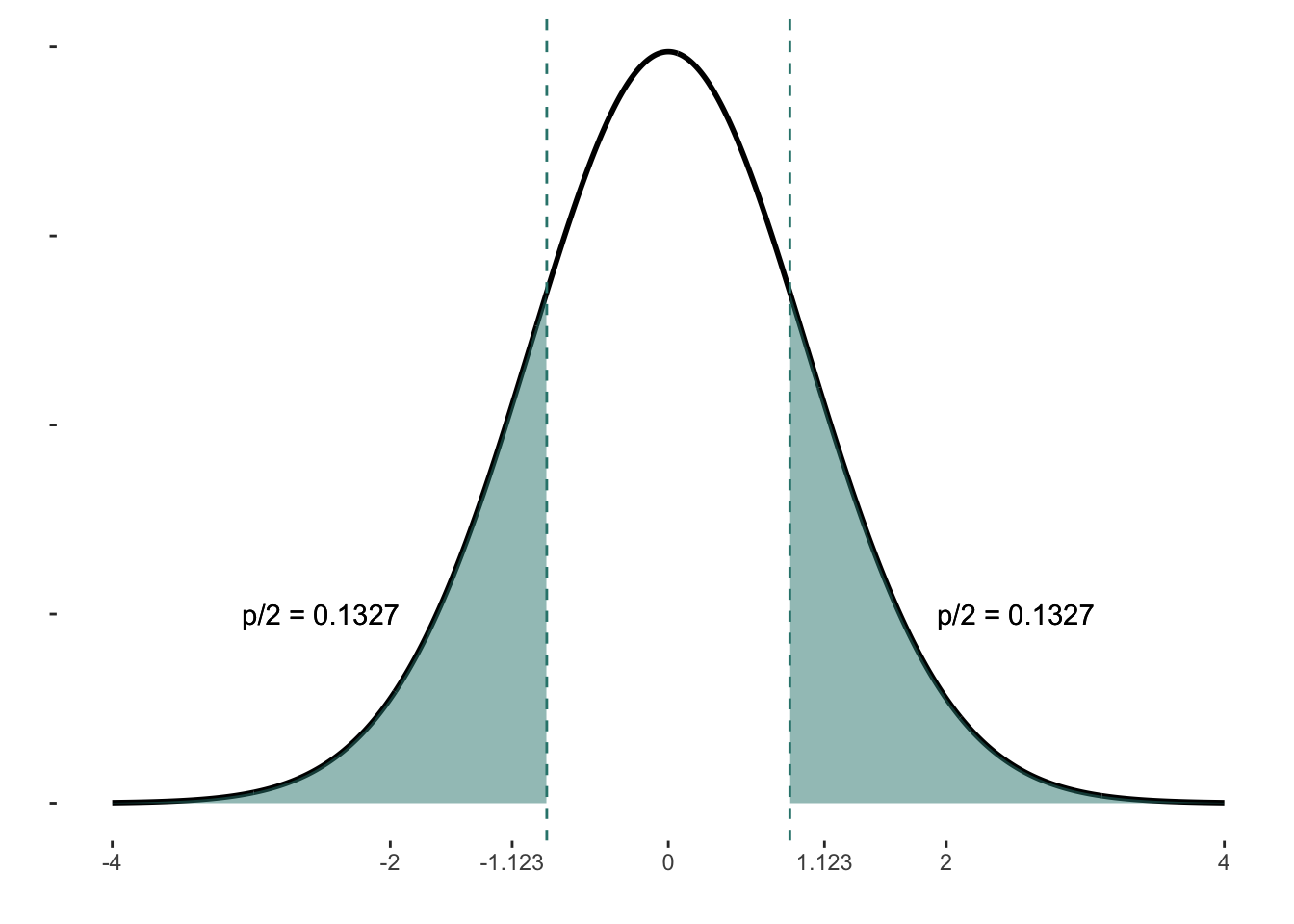
Kiegészítés 9.2 (Az egymintás t-próba p-értékének kiszámítása). Egy df = 67 szabadságfokú t-eloszláson mennyi a valószínűsége (probability) a t-próba értékének (-1,123331)?
Kétoldalú próba esetén egész pontosan:
\[ P(T ≤ -1.1233306) + P(T ≥ 1.1233306) \]
Ez az érték pedig 0,132653 + 0,132653 = 0,265306.
9.2 Egymintás z-próba
Egymintás z-próbát abban az esetben végzünk, ha a mintánk átlagát és szórását szeretnénk összevetni egy ismert populációátlaggal és populáció szórással.
Például, ha egy konkrét tesztpontszámot szeretnénk összehasonlítani az országos átlaggal és szórással, vagy a tesztkészítő ismert normájával.
Az egymintás z-próba is parametrikus teszt, vagyis azt feltételezi, hogy a mintánkban vizsgált változó egy meghatározott eloszlást (ez esetben normál eloszlást) követ.
Példa 9.3 (Példa egymintás elrendezésre populációátlag és -szórás ismeretében) Szakirodalmi adatok alapján tudjuk, hogy a FÉLNE-8 kérdőívvel mért félelem a negatív megítéléstől átlagpontszáma major depressziós esetén 17,00 és szórása 8,60 (Carleton és mtsai., 2011).
Klinikánkon csoportot indítunk major depresszióval diagnosztizáltak részére (F32.XX), és szeretnénk megnézni, hogy az általunk mért félelem a negatív megítéléstől átlagpontszám különbözik-e a szakirodalmi átlagtól.
Állítsuk fel a hipotéziseket kétoldalú próba esetére!
- Nullhipotézis (H0): A minta átlaga megegyezik a populáció ismert átlagával (μ = 17,00, 𝜎 = 8,60).
- Alternatív hipotézis (H1): A minta átlaga különbözik a populáció ismert átlagától (μ ≠ 17,00, 𝜎 ≠ 8,60).
Vizsgáljuk meg az előfeltételeket!
A változó skála típusú?
Igen, mert a FÉLNE-8 kérdőív Likert skála, tehát itemei ugyan ordinális változók, de a belőlük képzett összpontszám intervallumskálaként kezelhető.
A minta normál eloszlású?
Shapiro-Wilk teszttel ellenőrizzük a JASP szoftver segítségével a leíró statisztikák között vagy az egymintás próbára vonatkozó modulban az előfeltételvizsgálatok között.
A mintaelemek függetlenek egymástól?
Igen, mert a résztvevők különböző személyek, és a kutatási terv alapján biztosítottuk a függetlenséget.
A populáció szórása ismert?
Igen, a populáció szórása ismert.
A változó nem tartalmaz extrém értékeket?
Boxplot segítségével ellenőrizzük, vagy IQR módszerrel.
Állítsuk be a JASP-ban a próbát!
A hipotézis felállítását JASP-ban a következők szerint végezhetjük el:
A populáció ismert változóit (ti. átlag, szórás) beállítjuk a „Test value” és „Std. deviation” mezőben.
A megfelelő alternatív hipotézist jelöljük az „Alternative Hypothesis” rovatban
A Shapiro–Wilk-féle normalitásvizsgálatot az „Assumption checks” szekció „Normality” kipipálásával futtathatjuk.
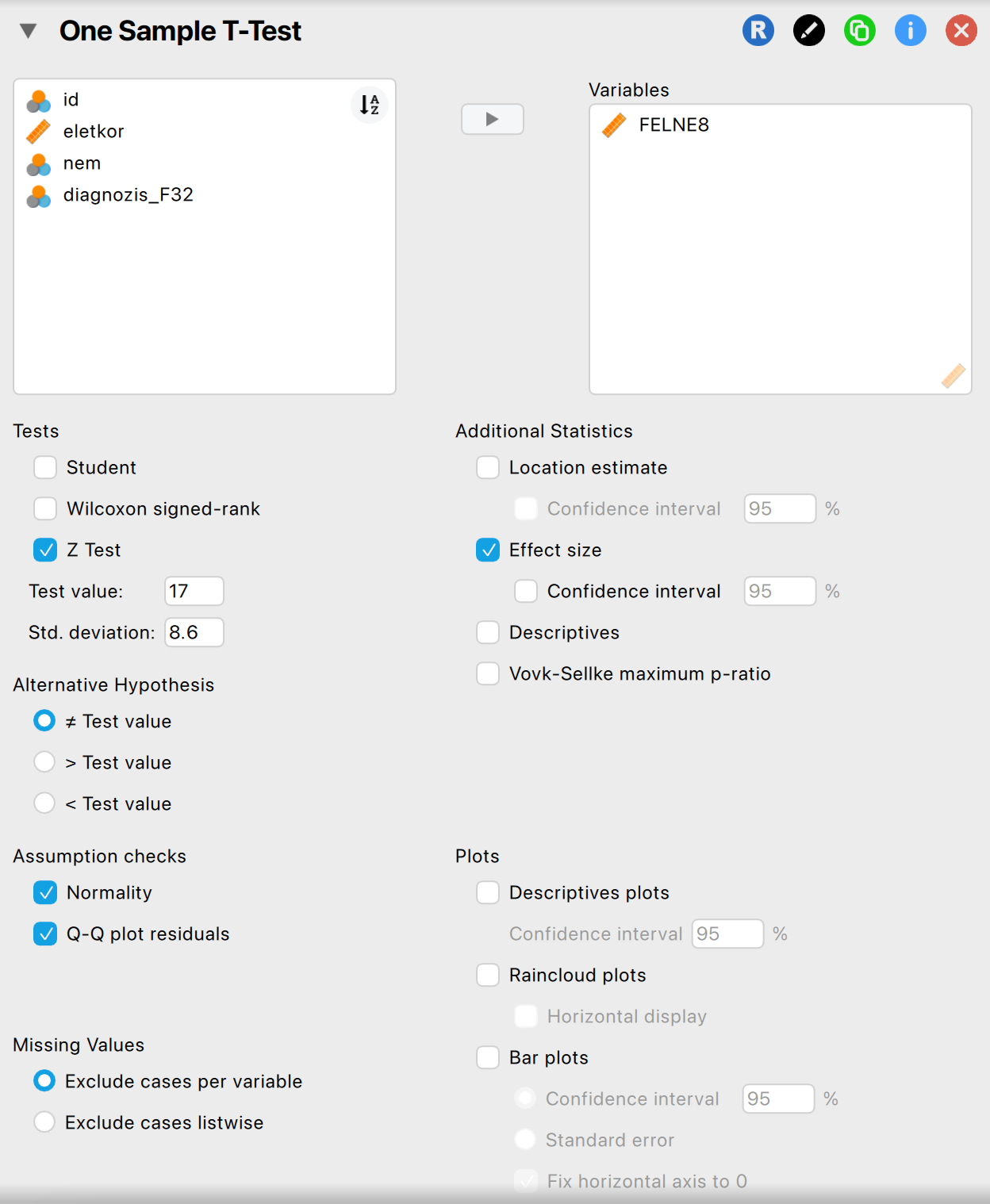
Beállítások: alternatív hipotézis, normalitásvizsgálat, hatásnagyság, tesztérték és szórás Olvassuk le és értelmezzük az eredményt!
Előfeltételvizsgálat: normalitás
Először a normalitásvizsgálat eredményeit olvassuk le. Ugyanis, ha nem követ normál eloszlást a vizsgált változónk, akkor az egymintás Wilcoxon-féle előjeles rangpróbát kellene használnunk, nem pedig a z-próbát.

A normalitásvizsgálat eredményei Az eredményeket leolvasva láthatjuk, hogy a Shapiro-Wilk próba nem szignifikáns (azaz \(p > 0,05\)), mert 0,177. Tehát a változónk normál eloszlást követ 4.
A Q-Q plot szemrevételezése alapján látjuk, hogy az adatok legnagyobb részt a vörös színű átlón mozognak, egyértelmű alakeltérés nem észlelhető.
A z-próba eredményének leolvasása

A z-próba eredménye A JASP a megjegyzések között jelzi nekünk az alábbi fontos figyelmeztetéseket:
Z-próbát alkalmazunk (“Z-test”)
Az alternatív hipotézisünk a 17,00 átlagértékhez viszonyít kétoldalasan. (“For the Z-test, the alternative hypothesis specifies that the mean is different from 17.”)
Így tehát amit leolvasunk a táblából, az ezekkel a figyelmeztetésekkel együtt értelmezendő:
A z-próba z-statiszikája: -0,874. Hogyan jött ki?
A p-érték: 0,382. Tehát a próba nem szignifikáns, vagyis \(p > 0,05\). Hogyan jött ki?
Cohen-d hatásnagyság: -0,106. Ez Cohen (1988) alapján elhanyagolható hatásnagyságnak tűnik.
Megoldás 9.3. A mintánk átlaga és szórása (M = 16,09, SD = 6,69) nem tér el szignifikánsan a norma szerinti 17,00-s átlagtól és 8,60 szórástól (z = -0,874, p = 0,382, d = -0,106).
Kiegészítés 9.3 (Az egymintás z-próba z-értékének kiszámítása). \[ z = \frac{\bar{x} - \mu_0}{\frac{\sigma}{\sqrt n}} \]
ahol
\(\bar{x}\) a mintánk átlaga (= 16,088),
\(\mu_0\) az ismert populációátlag (= 17,00),
\(\sigma\) a populáció szórása (= 8,60) (Vegyük észre, hogy ebben különbözik a t-próbától, mert ott a minta szórásával számoltunk!),
\(\sqrt n\) pedig a mintaelemszám négyzetgyöke (= 8,246).
Az egyenlet eredménye: -0,8742563.
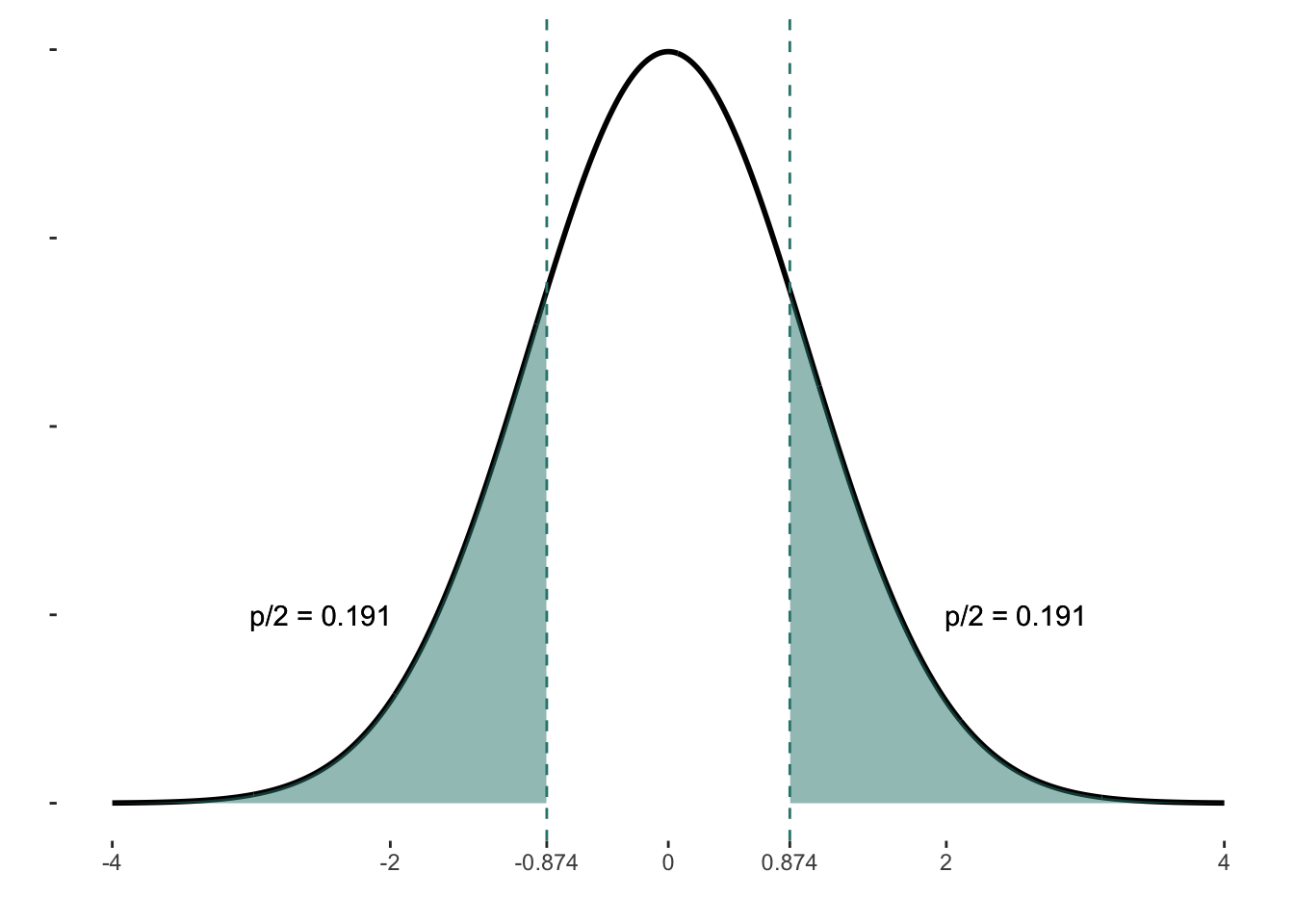
Kiegészítés 9.4 (Az egymintás z-próba p-értékének kiszámítása). Egy normál eloszláson mennyi a valószínűsége (probability) a z-próba értékének (0,8742563)?
Kétoldalú próba esetén egész pontosan:
\[ P(Z ≤ -0.8742563) + P(Z ≥ 0.8742563) \]
Ez az érték pedig 0,1909893 + 0,1909893 = 0,3819787.
9.3 Egymintás nemparametrikus próbák: egymintás Wilcoxon-féle előjeles rangpróba
Amennyiben a parametrikus próbák feltétele (vagyis ez esetben a normál eloszlás) nem áll fenn, nemparametrikus próbát kell alkalmaznunk, ami mögött nincs adott eloszlás feltételezése, de cserébe nem is tud kiindulni az átlagból mint középértékmutatóból (főleg, hogy az várhatóan nem eléggé középtájon helyezkedik el, mint normál eloszlás estén), helyette a mediánt használja majd.
Az egymintás Wilcoxon-féle előjeles rangpróba5 (one-sample Wilcoxon signed rank test) feltételei:
A vizsgált változó legalább ordinális, de lehet intervallum- vagy arányskála is.
A vizsgált változó nem kell normál eloszlást kövessen, de a próba feltételezi, hogy az eloszlás alakja szimmetrikus. Ha az eloszlás nem szimmetrikus, akkor előjelpróbát (sign test) kell alkalmaznunk.
A mintaelemek függetlenek egymástól. Ezt a kutatási terv alapján biztosítjuk.
A populáció szórása ismeretlen.
Kétoldalú próba esetén a nullhipotézis azt állítja, hogy a minta mediánja megegyezik a populáció ismert mediánjával, míg az alternatív hipotézis szerint a két medián különbözik egymástól.
Egyoldalú próba esetén értelemszerűen az alternatív hipotézis azt feltételezi, hogy a minták mediánja nagyobb/kisebb, mint a populáció ismert mediánja.
A szimmetrikusság ellenőrzésére az alábbi gyakorlati tapasztalati eszközeink vannak:
hisztogram és sűrűségfüggvény szemrevételezése
boxplot esetén a medián vonala nagyjából a doboz középtájékán helyezkedik el és a bajszok nagyjából azonos hosszúságúak
Ferdeség (skewness) > 1 vagy < -1 már erős asszimetriát jelez.
Statisztikai próbák, amelyek R-ben futtathatók (lawstat::symmetry.test()):
Miao-Gel-Gastwrith-féle szimmetriavizsgálat (Miao és mtsai., 2006)
Mira-féle szimmetriavizsgálat (Mira, 1999)
Cabilio-Masaro-féle szimmetriavizsgálat (Cabilio & Masaro, 1996)
Példa 9.4 A fejezet elején bemutatott kutatásunk adatait a példa érdekében lecseréljük (de a kutatási elrendezés változatlan marad) nem normál eloszlású válaszokra.
| Statistic | FELNE8 |
|---|---|
| N | 68.000 |
| Missing | 0.000 |
| Mean | 17.324 |
| SE (Mean) | 0.255 |
| SD | 2.105 |
| SE (SD) | 0.182 |
| Variance | 4.431 |
| SE (Var) | 0.766 |
| Median | 17.500 |
| Min | 12.000 |
| Max | 22.000 |
| IQR | 2.250 |
| Q1 (25%) | 16.000 |
| Q3 (75%) | 18.250 |
| Skewness | -0.294 |
| SE (Skew) | 0.291 |
| Kurtosis | 0.133 |
| SE (Kurt) | 0.574 |
| Shapiro W | 0.964 |
| Shapiro p | 0.048 |
Az adatfájl letölthető: FELNE8_onesample_F32_nonparametric.sav
Megoldás 9.4. A vizsgálatban (N =) 68 fő vett részt, közülük 34 nő (50,0%) és 34 férfi (50,0%). A vizsgált személyek átlagéletkora (M =) 35,01 év (SD = 3,19). A mintában a szociális szorongás átlagpontszáma (M =) 17,32 (SD = 2,11, Med = 17,50). A változó nem követi a normál eloszlást (W(68) = 0,964, p = 0,048).
Példa 9.5 (Példa egymintás elrendezésre nemparametrikus eljárással: egymintás Wilcoxon-féle előjeles rangpróba) Szakirodalmi adatok alapján tudjuk, hogy a FÉLNE-8 kérdőívvel mért félelem a negatív megítéléstől átlagpontszáma major depressziós esetén 17,00 (Carleton és mtsai., 2011).
Klinikánkon csoportot indítunk major depresszióval diagnosztizáltak részére (F32.XX), és szeretnénk megnézni, hogy az általunk mért félelem a negatív megítéléstől átlagpontszám különbözik-e a szakirodalmi átlagtól.
A feltételek teljesülését a példában most nem ellenőrizzük, de fontos előfeltétel a mintaelemek függetlensége, anélkül a nemparametrikus egymintás próba sem futtatható!
Ellenőrizzük a nemparametrikus próba feltételeit:
A vizsgált változó legalább ordinális?
Igen, a változó intervallumskála.
A vizsgált változó nem normál eloszlást követ, de szimmetrikus?
Ezt a JASP-ban ellenőrizzük:
Leíró statisztikai modulban
- hisztogram és sűrűségfüggvény ábrát szemrevételezzük
- boxplot ábrát szemrevételezzük
- ferdeségi (skewness) értéket ellenőrizzük
R modulban statisztikai próbát futtatunk. (Ez haladó szint!)
A mintaelemek függetlenek egymástól?
Igen, mert a résztvevők különböző személyek, és a kutatási terv alapján biztosítottuk a függetlenséget.
A változó nem tartalmaz extrém értékeket.
Ezt a boxplot ábrán ellenőrizzük.
Állítsuk be a JASP-ban a próbát!
A hipotézis felállítását JASP-ban a következők szerint végezhetjük el:
A populáció ismert változóját (ti. átlag) beállítjuk a „Test value” mezőben.
A megfelelő alternatív hipotézist jelöljük az „Alternative Hypothesis” rovatban.
A Shapiro–Wilk-féle normalitásvizsgálatot az „Assumption checks” szekció „Normality” kipipálásával futtathatjuk.
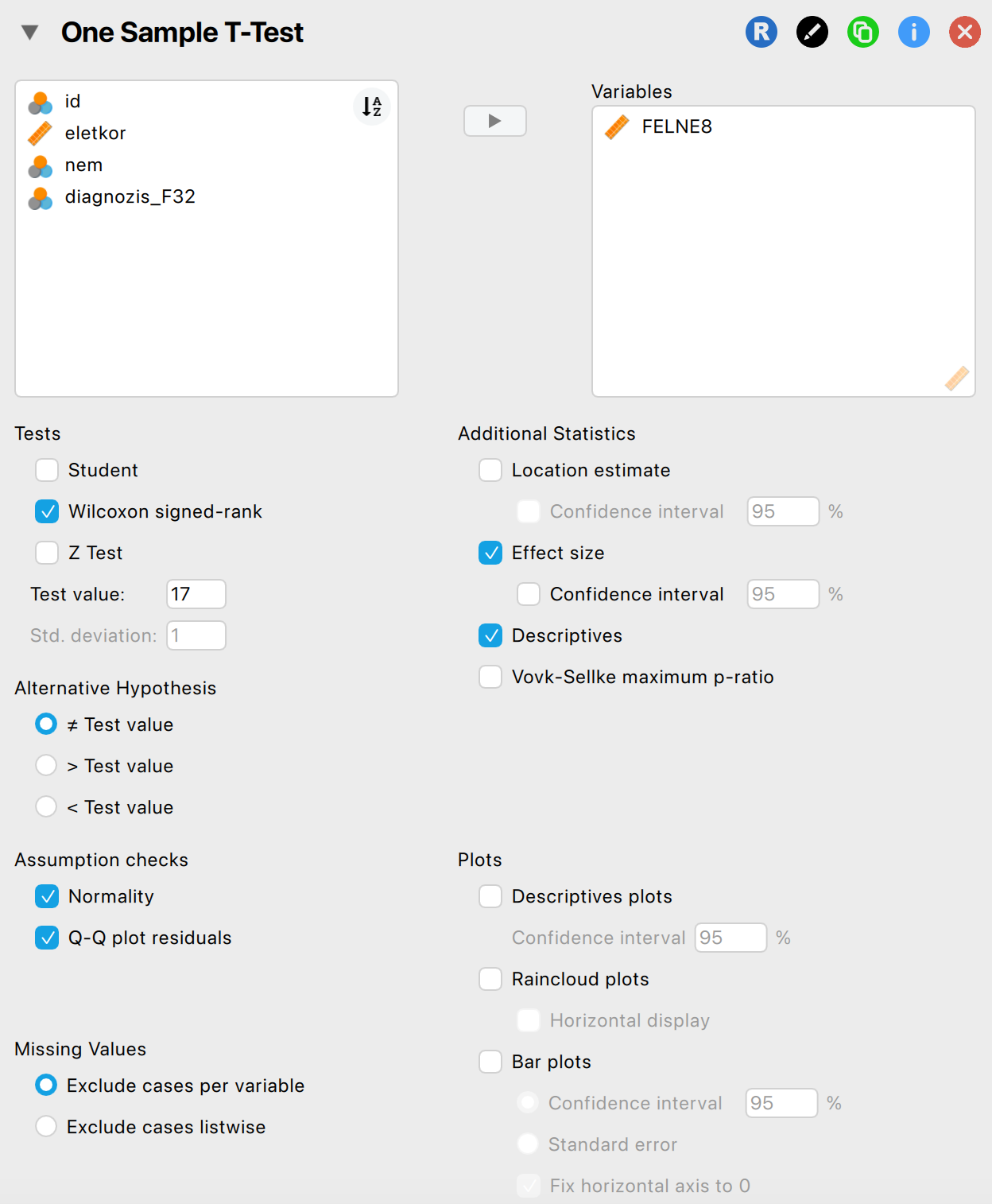
Beállítások: alternatív hipotézis, normalitásvizsgálat, hatásnagyság, tesztérték Olvassuk le és értelmezzük az eredményt!
Előfeltételvizsgálat: normalitás
Először a normalitásvizsgálat eredményeit olvassuk le.
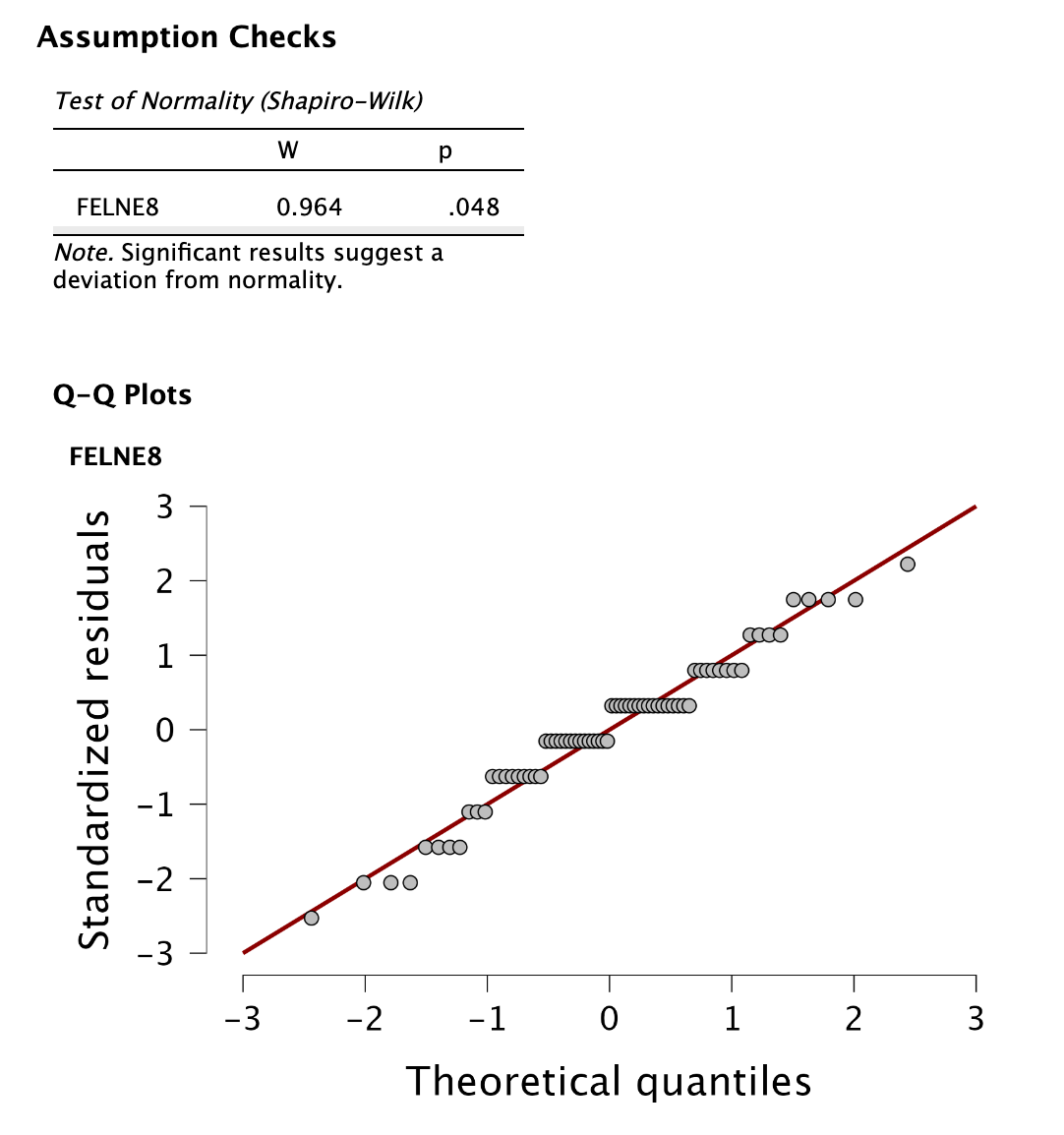
A normalitásvizsgálat eredményei Az eredményeket leolvasva láthatjuk, hogy a Shapiro-Wilk próba szignifikáns (azaz \(p < 0,05\)), mert 0,048. Tehát a változónk nem követi a normál eloszlást.
A Q-Q plot szemrevételezése alapján látjuk, hogy az adatok disztinkt mintázattal rendelkeznek és nem követik szabályosan az átlót.
Előfeltételvizsgálat: szimmetrikusság
A Descriptive Statistics modulban hisztogramot és sűrűségfüggvényt generálunk (Distribution plots és Display density).
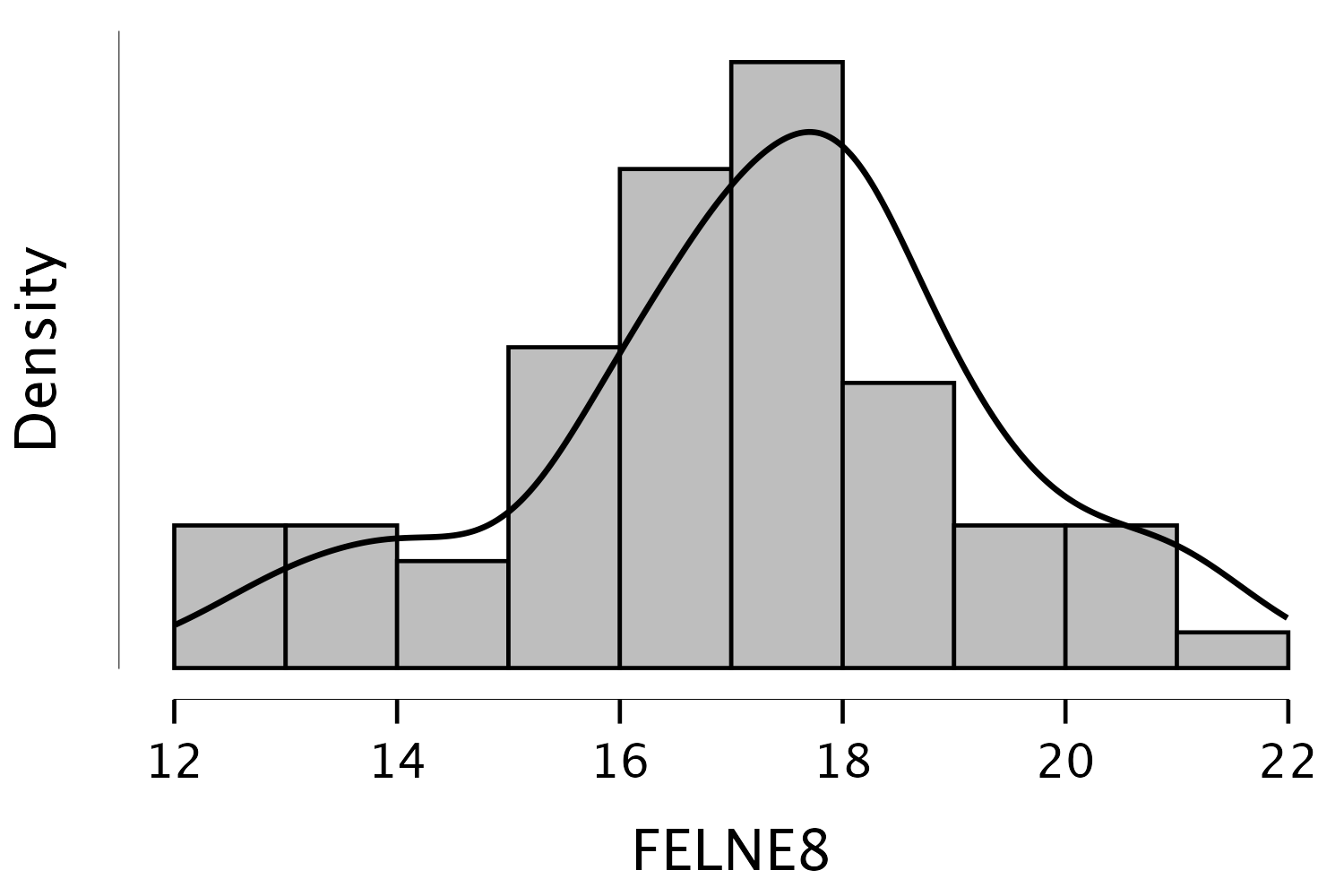
Hisztogram és sűrűségfüggvény Szemrevételezéssel láthatjuk, hogy a görbe nagyjából szimmetrikus.
A Descriptive Statistics modulban boxplotot generálunk.
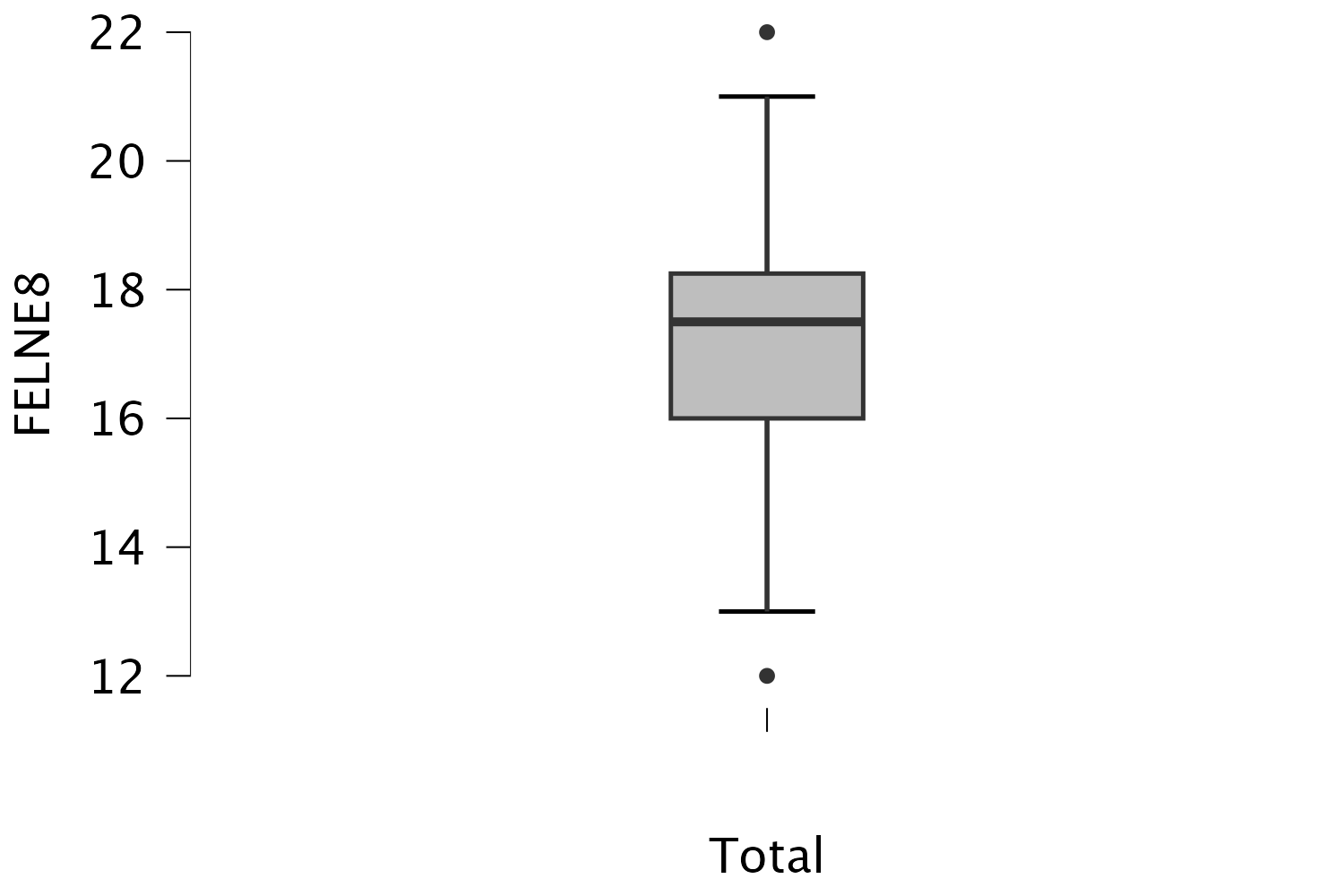
Boxplot Azt láthatjuk, hogy a medián vonala a középvonaltól kissé távolabb helyezkedik el, de a kétoldali bajusz hasonló hosszúságú.
A leíró statisztikák között látjuk, hogy a ferdeség -0,294, ami < 1 és > -1.
Ezek alapján feltételezhetjük az adatok szimmetriáját.
Haladó módszer: szimmetriapróbát futtatunk a Remark 9.5 részben leírtak szerint.
A rangpróba eredményének leolvasása
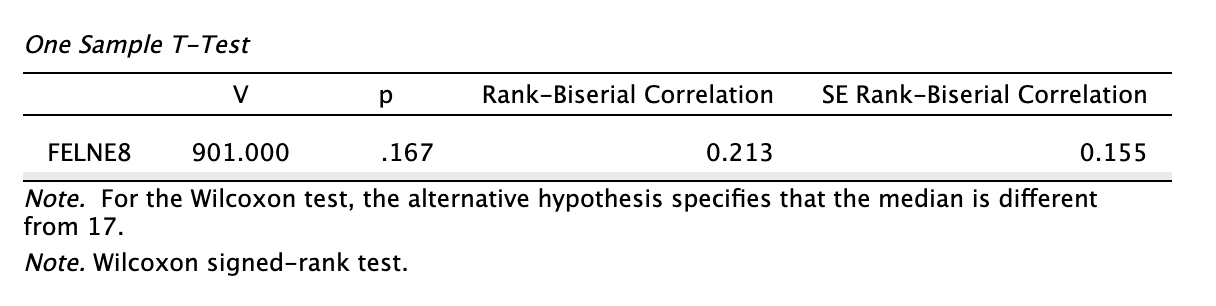
A rangpróba eredménye A JASP a megjegyzések között jelzi nekünk az alábbi fontos figyelmeztetéseket:
Wilcoxon próbát alkalmazunk (“Wilcoxon signed-rank test”)
Az alternatív hipotézisünk a 17,00 átlagértékhez viszonyít kétoldalasan. (“For the Wilcoxon test, the alternative hypothesis specifies that the mean is different from 17.”)
Így tehát amit leolvasunk a táblából, az ezekkel a figyelmeztetésekkel együtt értelmezendő:
Az egymintás Wilcoxon-féle előjeles rangpróba statiszikája: V = 901,000. Hogyan jött ki?
A p-érték: 0,167. Tehát a próba nem szignifikáns, vagyis \(p > 0,05\). Hogyan jött ki?
Rang-biszeriális korrelációs hatásnagyság: 0,213. Ez Cohen (1988) alapján kis hatásnagyság. A próba hatásnagyságát rang-biszeriális korrelációval számoljuk, így a korrelációs együtthatóra vonatkozó értelmezést használjuk, amelyből szintén használhatjuk a Cohen-féle változatot.
Megoldás 9.5. Egymintás Wilcoxon-féle rangpróba eredménye alapján a mintánk mediánja (Med = 17,50, M = 17,32, SD = 2,11) nem tér el szignifikánsan a norma szerinti feltételezett 17,00-s mediántól (V = 901,000, p = 0,167, rrb = 0,213).
Kiegészítés 9.5 (Szimmetriapróbák futtatása JASP-ban). A szimmetriapróbák nem részei a normál JASP moduloknak (a fejezet írásakor 0.95.4). Azonban a JASP a háttérben R-ben végez számításokat, és hozzáférést ad egy R konzolhoz is. Ez korlátozott funkcionalitású, de ezen belül elvégezhetőek a próbáink.
Telepítjük a megfelelő package-eket (csak első használat előtt)
Az alábbi kódokat futtatjuk:
install.packages("Kendall", repos = "https://cloud.r-project.org")install.packages("lawstat", repos = "https://cloud.r-project.org")Ezt követően a szimmetriát vizsgáló funkciót elindítjuk:
Például a FELNE8 változó esetén
lawstat::symmetry.test(data$FELNE8)A funkció automatikusan a Miao-Gel-Gastwrith-féle szimmetriavizsgálatot (Miao és mtsai., 2006) fogja futtatni.
A szimmetriavizsgálat eredményeit értelmezzük:
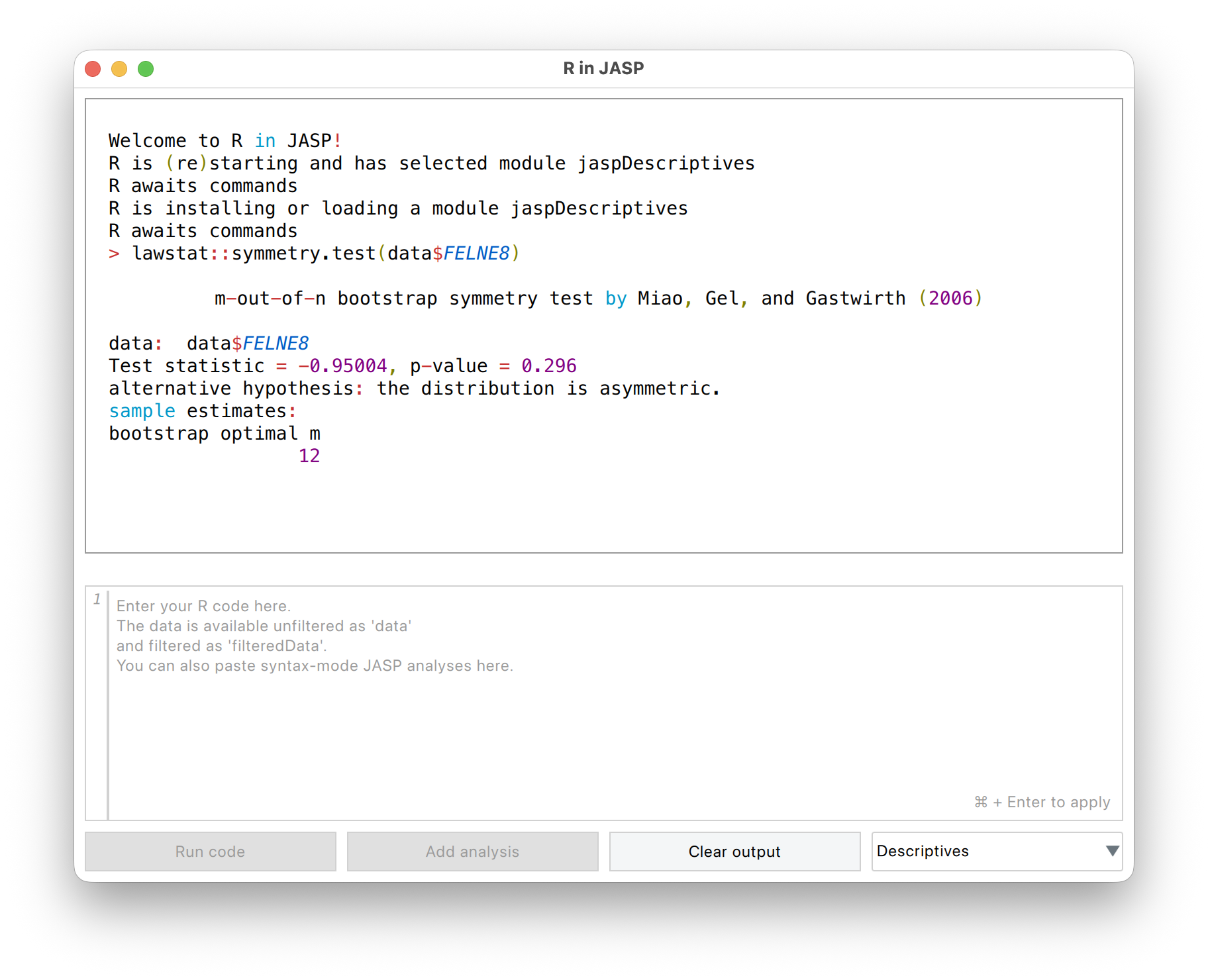
Miao-Gel-Gastwrith-féle szimmetriavizsgálat eredménye A próba alapján láthatjuk, hogy a hipotézis az, hogy az eloszlásunk aszimmetrikus (asymmetric), tehát ha a próba p-értéke szignifikáns (p < 0,05), akkor valóban aszimmetrikus eloszlással állunk szemben. Ha nem szignifikáns (p > 0,05), akkor valószínűleg szimmetrikus az adataink eloszlása.
- A próba neve a fejlécben van megjelölve
- A próbastatisztika a Test statistic értéke
- A p érték a p-value értéke.
Ha a kapott p-érték, amit ugyanezen az adatfájlon teszteltél, eltér a fent láthatótól, az normális jelenség, ugyanis bootstrapping módszert használ a futtatott próba.
Kiegészítés 9.6 (Az egymintás Wilcoxon-féle előjeles rangpróba statisztikájának kiszámítása). A rangpróba elvégzése a következő algoritmus szerint működik:
- Mindegyik adatpontból kivonjuk a feltételezett középértéket (17,00).
\[ D_i = X_i - \mu_0 \]
Elvetjük azokat a Di értékeket, amelyek értéke 0 (vagyis nem különböznek a feltételezett középértéktől).
Növekvő sorrendbe állítjuk a különbségek abszolútértékét, vagyis a |Di| értékeket. Ha több azonos rangérték van, átlagolunk.
A felállított rangokhoz rendeljük hozzá az eredeti előjeleket (+ vagy -).
Kiszámoljuk a tesztstatisztikát:
- V+: a pozitív előjelű eltérések abszolút összege
- V-: a negatív előjelű eltérések abszolút összege
- V: a V+ és V- érték közül a kisebb lesz a tesztstatisztika
Kiegészítés 9.7 (Az egymintás Wilcoxon-féle előjeles rangpróba p-értékének kiszámítása). A kiszámított V statisztika alapján z-score-t számítunk:
\[ z = \frac{V - \mu_V}{\sigma_V} = \frac{V - \frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)}{24}}} \]
A kapott érték valószínűségét kiszámítjuk normál eloszláson.
Egyoldalú próba esetén: \(P(V ≤ z)\)
Kétoldalú próba esetén: \(2 \times P(V ≤ z)\)
9.4 Egymintás nemparametrikus próbák: előjelpróba
Amennyiben az egymintás Wilcoxon-féle előjeles rangpróbát sem tudjuk használni, mert a vizsgált változó eloszlásának alakja nem szimmetrikus, akkor előjelpróbát (sign test) kell alkalmaznunk.
Továbbra is fontos feltétel (mint minden egymintás elrendezésnél), hogy mintaelemek függetlenek legyenek egymástól. Ezt a kutatási terv alapján biztosítjuk.
Példa 9.6 Kutatásunk adatait a példa érdekében ismét lecseréljük (de a kutatási elrendezés változatlan marad) nem normál eloszlású válaszokra, amelyek alakja aszimmetrikus.
| Statistic | FELNE8 |
|---|---|
| N | 68.000 |
| Missing | 0.000 |
| Mean | 16.750 |
| SE (Mean) | 0.255 |
| SD | 2.105 |
| SE (SD) | 0.182 |
| Variance | 4.429 |
| SE (Var) | 0.765 |
| Median | 16.000 |
| Min | 13.000 |
| Max | 22.000 |
| IQR | 3.000 |
| Q1 (25%) | 15.000 |
| Q3 (75%) | 18.000 |
| Skewness | 0.311 |
| SE (Skew) | 0.291 |
| Kurtosis | -0.438 |
| SE (Kurt) | 0.574 |
| Shapiro W | 0.960 |
| Shapiro p | 0.029 |
Az adatfájl letölthető: FELNE8_onesample_F32_nonparametric_assym.sav
Megoldás 9.6. A vizsgálatban (N =) 68 fő vett részt, közülük 36 nő (52,9%) és 32 férfi (47,1%). A vizsgált személyek átlagéletkora (M =) 35,19 év (SD = 2,97). A mintában a szociális szorongás átlagpontszáma (M =) 16,75 (SD = 2,10, Med = 16,00). A változó nem követi a normál eloszlást (W(68) = 0,960, p = 0,029).
Példa 9.7 (Példa egymintás elrendezésre nemparametrikus eljárással: előjelpróba) Szakirodalmi adatok alapján tudjuk, hogy a FÉLNE-8 kérdőívvel mért félelem a negatív megítéléstől átlagpontszáma major depressziós esetén 17,00 (Carleton és mtsai., 2011).
Klinikánkon csoportot indítunk major depresszióval diagnosztizáltak részére (F32.XX), és szeretnénk megnézni, hogy az általunk mért félelem a negatív megítéléstől átlagpontszám különbözik-e a szakirodalmi átlagtól.
Ellenőrizzük a nemparametrikus próba feltételeit:
A vizsgált változó legalább ordinális?
Igen, a változó intervallumskála.
A vizsgált változó nem normál eloszlást követ és nem is szimmetrikus.
Ezt a JASP-ban ellenőrizzük:
Leíró statisztikai modulban
hisztogram és sűrűségfüggvény ábrát szemrevételezzük.
A Descriptive Statistics modulban hisztogramot és sűrűségfüggvényt generálunk (Distribution plots és Display density).
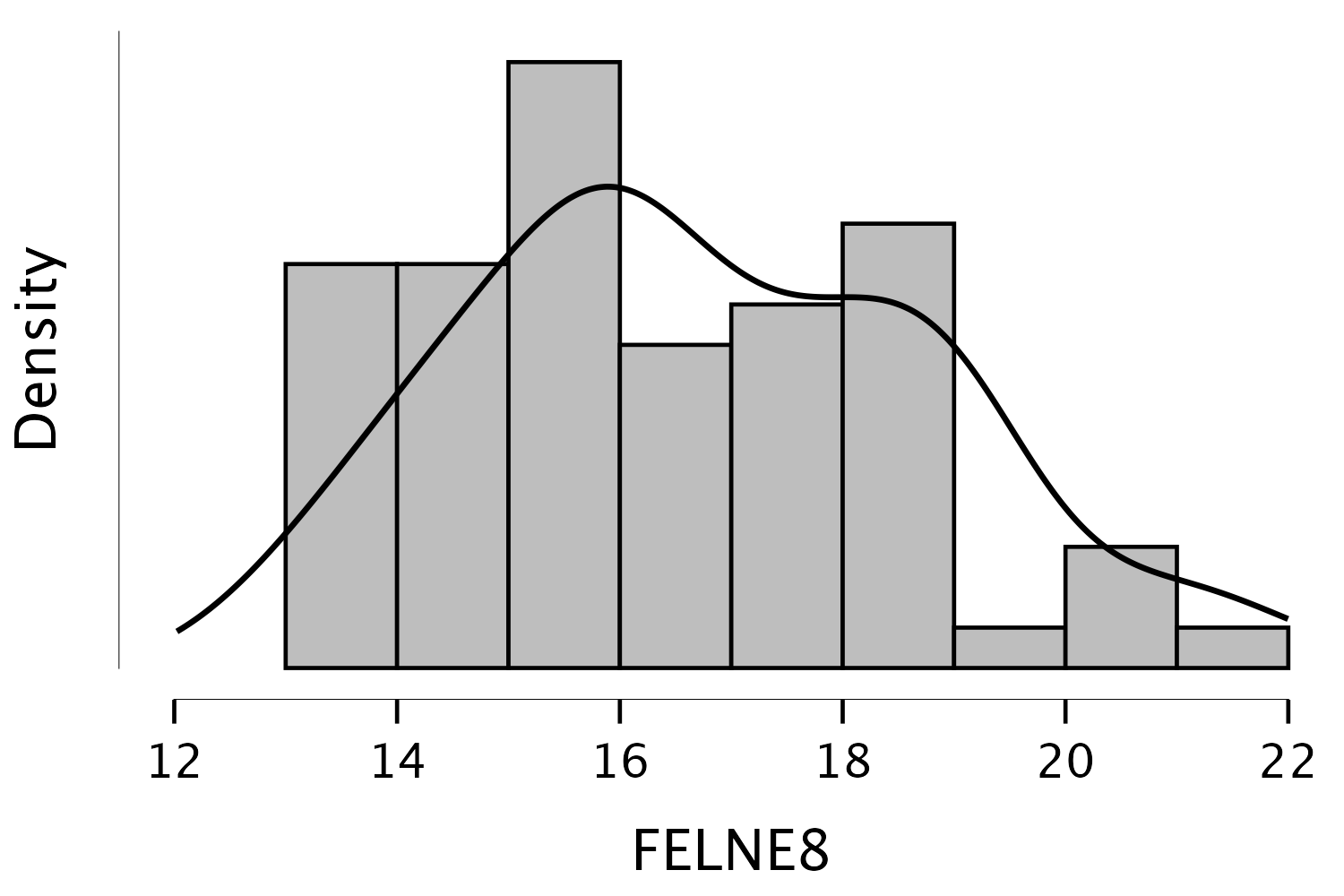
Hisztogram és sűrűségfüggvény Szemrevételezéssel láthatjuk, hogy a görbe nem szimmetrikus.
boxplot ábrát szemrevételezzük
Azt láthatjuk, hogy a medián vonala a középvonaltól távolabb helyezkedik el, és a kétoldali bajusz jelentősen eltérő hosszúságú.
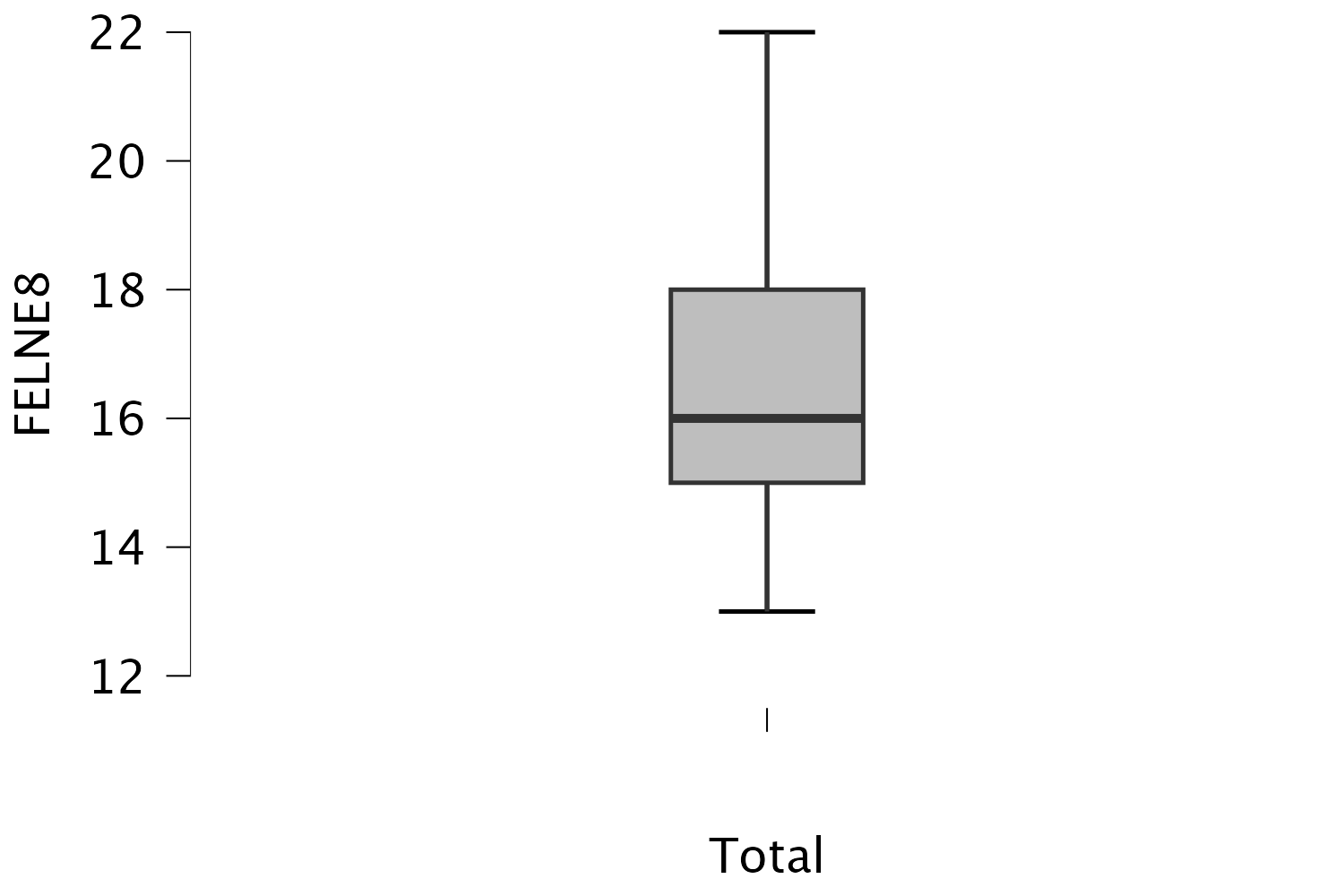
Boxplot ferdeségi (skewness) értéket ellenőrizzük
A leíró statisztikák között látjuk, hogy a ferdeség 0,311, ami < 1 és > -1.
Ezek alapján feltételezhetjük az adatok szimmetriáját, azonban az előző két módszer alapján mégsem.
R modulban statisztikai próbát futtatunk. (Ez haladó szint!)
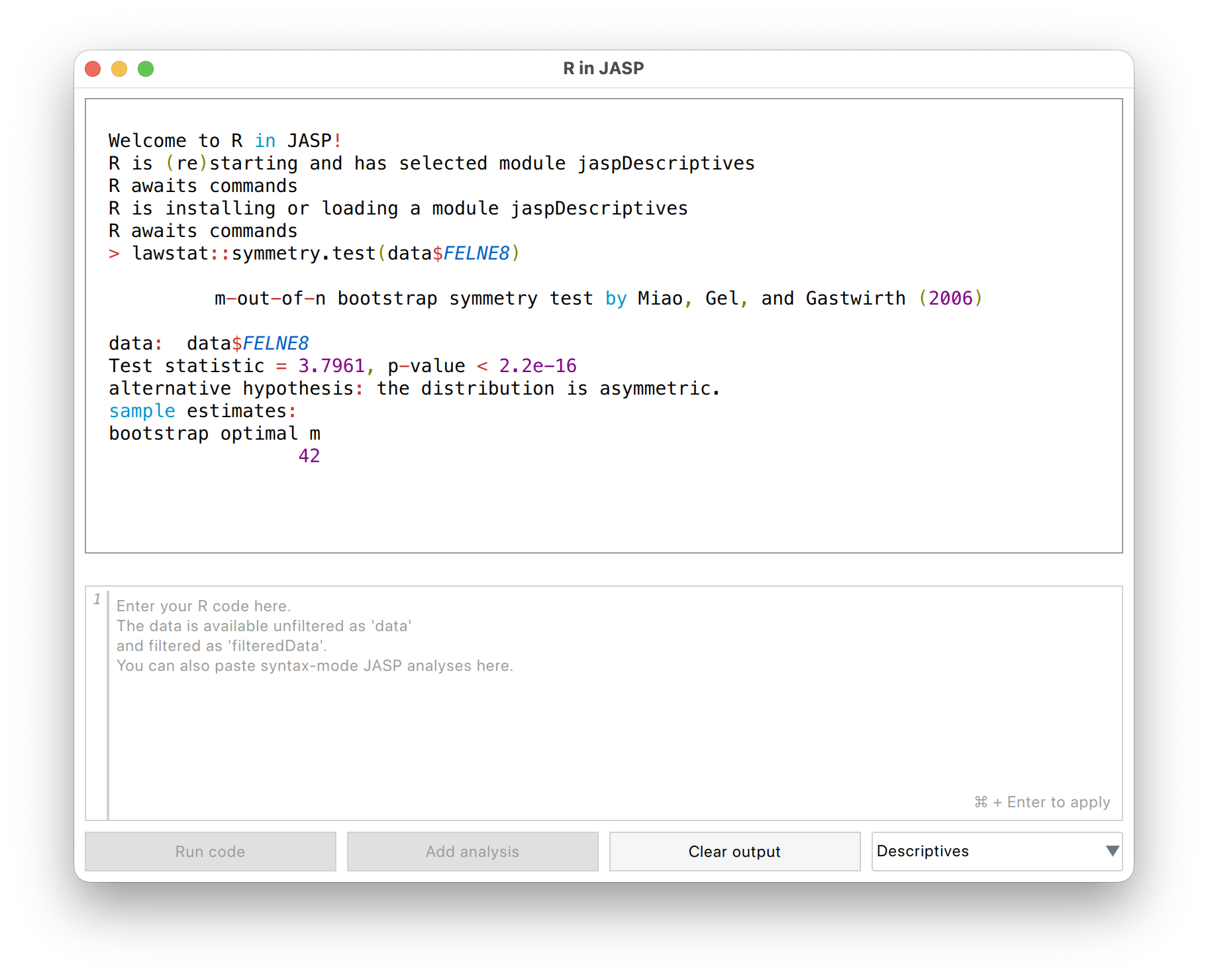
Miao-Gel-Gastwrith próba eredménye Ennek eredménye szignifikáns lesz, tehát meggyőződhetünk róla, hogy az adataink tényleg aszimmetrikusak, tehát csak az előjelpróba futtatható.
A mintaelemek függetlenek egymástól?
Igen, mert a résztvevők különböző személyek, és a kutatási terv alapján biztosítottuk a függetlenséget.
Állítsuk be a JASP-ban az előjelpróbát!
Mivel ez a próba nem része a JASP-nak a fejezet írásakor, az R konzolhoz kell fordulnunk.

R konzol JASP-ban Itt telepítenünk kell előbb az előjelpróbát tartalmazó package-t (csak első használat előtt):
install.packages("BSDA", repos = "https://cloud.r-project.org")A próba futtatásához a FELNE8 adatsoron a következő parancsot használjuk:
BSDA::SIGN.test(data$FELNE8, md = 17, conf.level = 0.95)Olvassuk le és értelmezzük az eredményt!
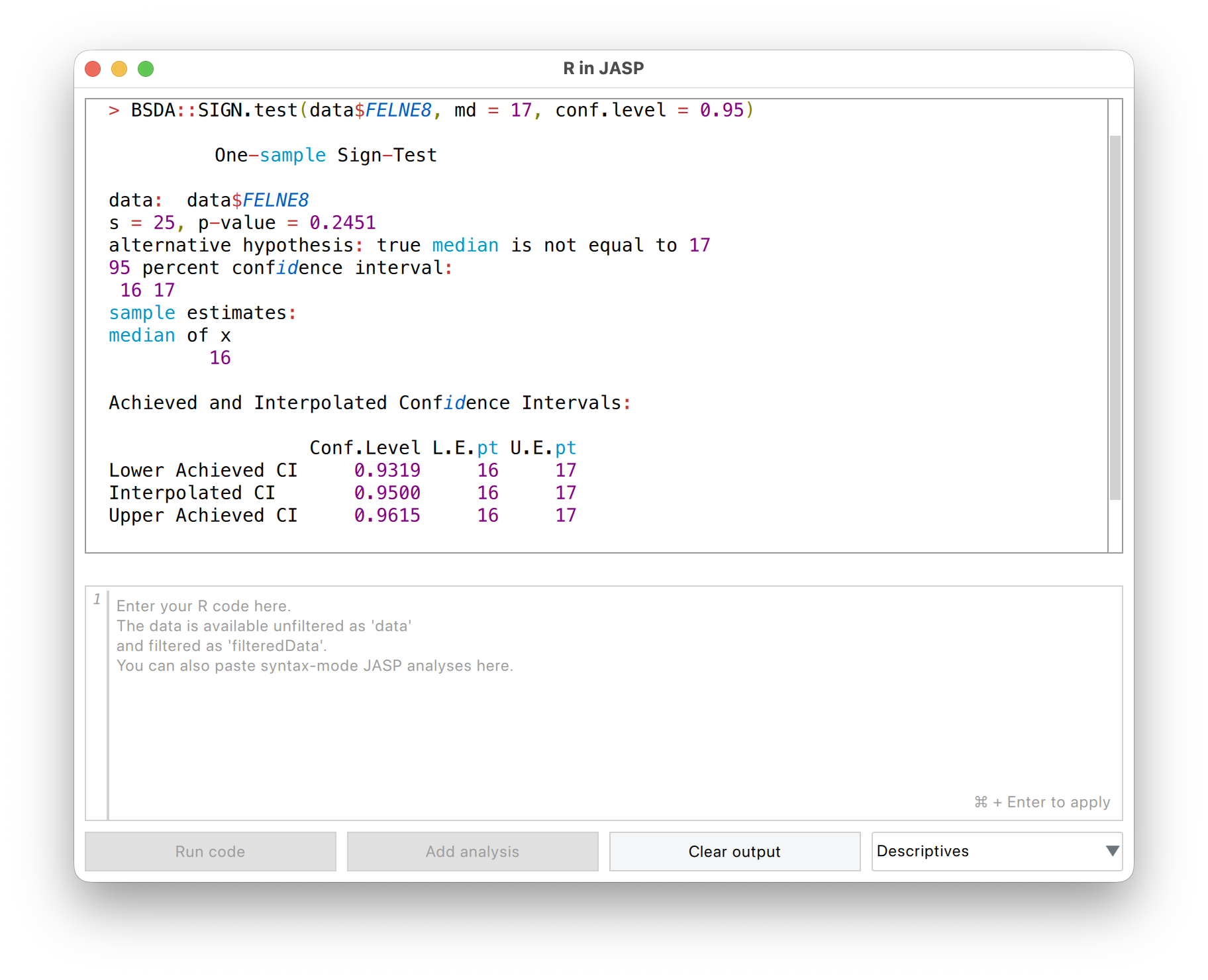
Az előjelpróba eredménye - A próba tesztértéke az s érték.
- A próba p értéke a p-value.
Megoldás 9.7. Egymintás előjelpróba eredménye alapján a mintánk mediánja (Med = 16,00, M = 16,75, SD = 2,10) nem tér el szignifikánsan a norma szerinti feltételezett 17,00-s mediántól (s = 0,245, p = 0,245).
Tegyünk úgy, mintha a szórást nem ismernénk.↩︎
Mert most úgy csinálunk, mintha nem lenne benne a hivatkozott cikkben a példa kedvéért.↩︎
A Shapiro-Wilk próba azt vizsgálja, hogy a mi változónk eloszlása eltér-e a normál eloszlástól, így ha szignifikáns a próba eredménye, akkor a változónk eltér a normál eloszlástól. Ezt a JASP is jelzi nekünk a “Significant results suggest a deviation from normality” megjegyzéssel.↩︎
A Shapiro-Wilk próba azt vizsgálja, hogy a mi változónk eloszlása eltér-e a normál eloszlástól, így ha szignifikáns a próba eredménye, akkor a változónk eltér a normál eloszlástól. Ezt a JASP is jelzi nekünk a “Significant results suggest a deviation from normality” megjegyzéssel.↩︎
Nem keverendő a „sima” Wilcoxon előjeles rangpróbával, ami a páros mintás elrendezések nemparametrikus tesztje.↩︎